You , are given an array of n elements and q queries . Both n and q can range upto 10^5 , and 1<=a[i] <= 10^9.
how to find / count all the elements less than a given element in each query .
queries are in the form of l , r , x where x is number and l and r are starting and ending indices.
Example: index 1 based
a[] = {5 , 3 , 2 , 2 , 3 , 1 , 2 , 9 , 10 , 2 }
q1 = 5 9 5
ans = 3 { 3 , 1 , 2}
q2 = 1 4 2
ans = 2 {2 , 2 }
The problem gives a feel of segment tree , but how to solve it using ST ?
any idea.
I don't know about segment tree, but it can be solved with SQRT decomposition and Mo's algorithm.
mo's algorithm ? how . can u explain . despotovski01
If you are not familiar with Mo's algorithm, there's a good tutorial on HackerEarth about it. Do coordinate compression on all possible values found in array or queries, so that the range of the values becomes [0, 2 * 105). Then, keep count array for the values and a decomposed version of the array, which has
blocks. Those arrays will keep track of the count of values for your queries. To calculate the total value of items less than x, you'll need just 
steps, because there are at most 
blocks, and at most 
values to be included that are not in a block. Total complexity is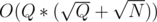 
Edit: now I noticed that you asked how to find those elements as well. Just modify the previous algorithm to store the elements in each block in some data structure that supports efficient add / remove operations. A linked list or a hash table would be a good choice, because linked lists support addition and deletion of elements to the head and tail in O(1).
You can solve each query in (logN)^2 using merge sort tree.
what is merge sort tree , i dont know .
in segment tree you have to keep a vector as a node element and each node of segment tree will have the sorted range of left and right sub tree. then you will have to query in L to R for that when you reach a segment that completely lies in the range you have to do a binary search for number of element less than x in that segment and like this you have to add the answers coming from all segments
you can have a look to this link : https://discuss.codechef.com/questions/94448/merge-sort-tree-tutorial
hey , cool . can you provide me some links from where u studied Merge sort tree .
the idea of segment tree + binary search is very intutive .
You can read about many applications from this site :
http://e-maxx.ru/algo/segment_tree
this can be done with a wavelet-tree
what is wavelet — tree ? i dont know . please give me the link to it
link
i got this blog . can anyone tell why we need to sort the array and querie. why sorting will not affect our answer
https://www.geeksforgeeks.org/number-elements-less-equal-given-number-given-subarray/
When you sort the array you also maintain the indices of the values. The BIT at each index basically stores whether that element is "active" in the array (0 or 1). Then to process the next query l, r, x, you "activate" every unactivated i such that ai < x by performing a point increment at every such i. To do so you just iterate through the sorted array. The answer to the query is then simply the range sum on the BIT over [l, r].
I think you're misunderstanding why the sorting is done. The sorting is necessary to perform the right updates for the next query. What makes you think it would affect the answer in any way?
Also note that this solution is offline unlike some of the suggestions you got.
Mo's algorithm + Fenwick tree
There exist a version of this problem with update query you can find it in Vietnamese-SPOJ It can be done using sqrt-decomposition + 2d BIT. The idea is to divide the sequence in to sqrt(N) blocks, and you maintain the numbers of value which is greater than a specific value by a BIT. You can find my implementation for it here
I see that same question asked every week... You can always use google to find a solution for such standard problems.
I'm not sure if it's possible to solve this with a Segment Tree. I know for a fact that you can solve it by compressing the coordinates and using a Persistent Segment Tree, however, it seems like an overkill to me. I'd use a Wavelet Tree to solve this problem.
you can solve it using segment tree + coordinate compression.
first we will make coordinate compression because values of a[i] is large (10 ^ 9) , so we will have new idx for every number.
after that we will build the segment tree where tree[node] = tree[node * 2] + tree[node * 2 + 1]
after that we will make query as it's sum problem that will return number of elements <= new idx of current element