UPD. Все, что будет описано ниже, давным давно делает tourist, например, в последней своей посылке.
В древних задачах на сайтах acmp, e-olymp и timus часто ограничения по памяти крайне малы и равны 16 МБ, 32 МБ, 64 МБ. Скорее всего, для современных ограничений в 256 МБ и 512 МБ описанный ниже способ достижения минимального потребления памяти под дерево отрезков не актуален, но все же рассмотрим способ, позволяющий его достичь в реализации сверху-вниз. Будем использовать ровно 2·n - 1 узлов, а вершины пронумеруем в порядке эйлерова обхода:
0
1 8
2 5 9 10
3 4 6 7
Тогда, если мы находимся в узле v и это не лист, то у него есть левое и правое поддеревья. Номер левого поддерева равен v + 1, так как в порядке эйлерова обхода мы посетим его сразу после текущего узла. Что касается правого поддерева, то туда мы пойдем только когда посетим корень и все вершины левого поддерева. Количество вершин в поддереве зависит только от длины отрезка, соответствующего узлу дерева.
Будем считать, что если у нас есть отрезок [l, r], то левому поддереву соответствует отрезок [l, m], а правому — [m + 1, r], где m = (l + r) / 2. Тогда длина левого отрезка будет равна m - l + 1, а количество узлов в нем 2·(m - l + 1) - 1.
Окончательно получаем, что для узла v, соответствующего отрезку [l, r], левое поддерево в нумерации в порядке эйлерова обхода будет иметь номер v + 1, а правое — номер v + 2·(m - l + 1), где m = (l + r) / 2 — середина отрезка [l, r].











http://codeforces.net/blog/entry/18051 — same tree with different traversal
Simple and great idea! But I didn't get the last line.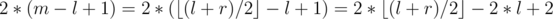 which is r - l + 2 if l and r have same parity and r - l + 1 otherwise.
which is r - l + 2 if l and r have same parity and r - l + 1 otherwise.
Looks like I forgot to multiply on 2 after division. I mean that we need to add 2·leftLen to v, but leftLen is the half of rootLen = r - l + 1 after division. Correct formula is
v + (r - l + 1 + 1) / 2 * 2 = v + (r - l) / 2 * 2 + 2, so with midpoint formula looks more easy, I will remove last abstractThis idea is mostly based on cache locality rather than memory consumption.
I've seen this while studying cache-oblivious data structures. Such tree works significantly faster than most others, because it is cache-friendly. (subtree of vertex v contains of some interval [l..r])
Had some benchmarks made for such tree, but can't find them right now.
Sorry, can't reproduce speed up from cache optimizations. Tried on problem with 1.000.000 items and queries increment values on segment by constant and get maximal value on segment.
0.7 svs0.7 sfor both orders: Euler Tour order, simple orderCan you, please, found experiments what you did?