deva2802's blog

Invitation to CodeChef February Cook-Off 2019 sponsored by ShareChat!
By deva2802, history, 6 years ago, In English

Greetings Codeforces community! You are all invited to CodeChef’s February Cook-Off sponsored by ShareChat. The Cook-Off is a short contest that lasts 2.5 hours and features 5 problems for you to try and solve. The contest problem statements are available in English, Hindi, Bengali, Russian, Mandarin and Vietnamese.

ShareChat — India’s fastest growing social network is offering exciting jobs and internships to the participants of the Cook-Off. Visit the contest link for more details.

I hope you will join your fellow programmers and enjoy the contest problems. Joining me on the problem setting panel are:

  • Tester: Deemo (Mohammad Nematollahi)
  • Editorialist: Pepe.Chess (Hussain Kara Fallah)
  • Statement Verifier: Xellos (Jakub Safin)
  • Setters: kingofnumbers (Hasan Jaddouh), deva2802 (Devanshu Agarwal), Pi-nan (Shivam Gor), Abhinav Jain
  • Mandarin Translator: huzecong (Hu Zecong)
  • Vietnamese Translator: Team VNOI
  • Russian Translator: Mediocrity (Fedor Korobeinikov)
  • Bengali Translator: solaimanope (Mohammad Solaiman)

  • Hindi Translator: Akash Shrivastava

    Contest Details:

  • Start Date & Time: 17th February 2019 (2130 hrs) to 18th February 2019 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone
  • Contest link: https://www.codechef.com/COOK103
  • Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
  • Prizes: Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. Know more here: https://www.codechef.com/laddu
    (For those who have not yet got their previous winning, please send an email to [email protected])

Good Luck!
Hope to see you participating!!
Happy Programming!!

  • Vote: I like it
  • +68
  • Vote: I do not like it

Comments Comments (23)
| Write comment?
»
6 years ago, # |
  Vote: I like it +22 Vote: I do not like it

The contest starts in 3.5 hours

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by deva2802 (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it +12 Vote: I do not like it

How do you solve EVILAND?

→ Reply
»
6 years ago, # |
← Rev. 4   Vote: I like it +3 Vote: I do not like it

How to solve Evil Land?

My solution: find the periodicity of F (i.e. ) then get the LCM of the periodicity of each Ai. Finally, remove elements from A which have (in their periodicity) a prime with power larger than the power of the same prime in the periodicity of F (try for each prime in F).

This gave TLE because I find the periodicity in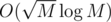 for each number.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    Why does taking the LCM help? I'm not able to understand what's going on.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 5   Vote: I like it 0 Vote: I do not like it

      If a number X has a periodicity P on a modulo M then Xi will equal all numbers Y such that Y has a periodicity Q where Q is a divisor of P. If two numbers a and b have a periodicity Pa and Pb then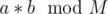 has a periodicity of LCM(Pa, Pb).

      So the problem is now to remove some elements of A such that the LCM of their periodicity of the remaining is not a multiple of the periodicity of F.

      To prove that, let X be a number which has a periodicity P and Xi equals Y which has a periodicity of Q. Then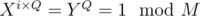 . Then 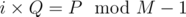, which means that Q is a divisor of P. Remember that both P and Q are divisors of M - 1 because Xφ(M) = 1.

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

When will the problems be available for practice?

→ Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +8 Vote: I do not like it

EVILAND: g(x, MOD) = periodicity of x in mod MOD. Make a[i] = g(a[i], MOD) and now the problem is removing some elements so that the lcm of the remaining elements isn't a multiple of g(F, MOD). Didn't submit because I started the contest in the last hour but I'm pretty sure this is correct. To prove this, transform multiplication to addition with a primitive root and the problem is the same but with addition.

How to solve TWOARR without persistent implicit treap or lazy updates with persistent seg tree? I solved it using lazy update with persistent seg tree but my constant was complete shit and it barely passed the TL with log^2 updates/queries.

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I did the same in EVILAND but got TLE.

    For TWOARR: sqrt-decomposition passed in ~2seconds

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +16 Vote: I do not like it

      You can preprocess the primes and find periodicity in log^2 like this

      int getId(int x, int MOD) {
	if(x == 0) {
		return 1;
	}
	int ans = MOD - 1;
	for(auto p : primes[MOD-1]) {
		while(ans % p == 0 && fexp(x, ans / p, MOD) == 1) {
			ans /= p;
		}
	}
	return ans;
}

      It solves each case in O(N*log^2).

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    Setter code for TWOARR was n*log^2 . It passes in 1.8sec.

    There exist sqrt deco solutions too.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How would you handle the queries using sqrt decomposition? especially the query of the first type.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Decompose array A, into root(n) blocks, then every query of type two can be handled in O(root(n)logn), using a flag to rebuild a block. For this we need to maintain a persistent seg tree on B. adjusting the Block size gives O(nroot(nlogn)) solution.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Yeah. Thought the same. just idea of persistent to handle the update of the value of b slipped out of my mind. Thanks.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            what is persistent st?

            → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Thanks for the problem, got my lazy ass to finally code persistent random BST. https://www.codechef.com/viewsolution/23140693 O(N * logN) expected time solution.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        hey u coded treap . whats the difference between persistance tree and treap are both same

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          They aren't. Persistent treap doesn't really work because expected height breaks when you merge a treap with itself (due to how priorities work in treaps) but you can use a different randomization during merge (that I really can't explain why it works other than it makes every node have the same probability of being the root in a subtree). This different randomization is leftSide function in my code, I think you can't call this a treap anymore since it doesn't have heap properties.

          → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

For EVILAND I found primitive root and all its degrees, and sorted that information, that allows to find the discrete log for each number in O(1), giving MlogM + N overall, which passed for me

→ Reply
»
6 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Almost a week since the contest and I still can't find the EVILAND editorial.

→ Reply