Hi all,
The third contest of the 2018-2019 USACO season will be running from February 22nd through February 25th, and will be the final regular contest before the US Open. Good luck to everyone! Please wait until the contest is over for everyone before discussing problems here.
Edit 1: The contest will open soon! If you see any issues with any of the problems, please follow the instructions here letting the contest director know what issues you have. Please do not complain about them on this blog post — that may spoil the problems for other contestants and it will not result in your issues being resolved. Good luck to all contestants!
Edit 2: The contest will end in under 24 hours! As a reminder, since all contestants get a full four hour contest window irrespective of when they start, please hold off discussion of the contest until everyone has finished the contest (4 AM UTC-12).











is it rated?
This has a whole new meaning now lol
I honestly don't find any point in these type of blogs because people who are actually gonna take the contest probably already know when they can take the contest.
People use these blogs to discuss the problems after the contest window ends as well.
I'm gonna participate in this one and didn't know when it was so thanks mr blog poster.
Can a non-US person take part in the US Open
Yes, US Open is exactly like a normal USACO contest but is longer (5 hours instead of 4) and the problems are harder.
in the last contest i solved the 3rd gold problem and i submit it but it got wrong answer on the first test while the output was exactly same with the sample output,after the contest one of my friends told me that was because of an extra space in the end of my output :|
i've never seen a wrong answer because of such problems,if that problem didn't happens maybe this round i will compete in platinium
please fix that problems in this round
The grader is pretty specific about most output errors. If it were the same as the sample, extra spaces should've been your first guess.
i don't know why i didn't try extra space but i remember that i tried some other thing's like endl and when they didn't work i gave up
Contest should be over. Can anyone confirm?
Nope, people might still be taking the contest. Wait another 35 minutes.
I think there is 2hrs and 30mins before people are done taking the contest.
How do you solve Bronze Q1 (deque of cards) ?
Anyone know how to do Gold #2 or #3? Implementation for #1 took freaking forever, and I thought #3 was comp geo (speaking of which, wtf is comp geo doing in gold?)
Gold 2 was binary search
Gold 3 was rectangle dp
Shoot. Thought I had a binary search sol but doubted it would be in gold...
Can you explain #3 a bit more?
first mark all points on your grid
Find the points which have k intersections. Mark them as -1. Find the points with k-1 intersections. Mark them as 1. Mark the rest of the grid as 0.
Your problem reduces to finding 2 rectangles of maximum area after that
o fck that works
Yes, you use Kadane's algorithm in 2D on prefixes and suffixes. I actually only got 11/14 test cases because of a bug in my implementation :(
How do you make sure the second rectangle you find doesn't overlap with the first?
You essentially do a line sweep from both ends (left/right, up/down) and keep track of the best rectangle found by Kadane's algorithm so far. And then you simply iterate and do
ans = max(ans, left[i] + right[i + 1])(don't forget edge cases ofleft[200]andright[0]!) and same for up/down. You're splitting the table into two parts basically and finding best rectangle in each of them.Thanks
if you have 100,000 (max N) 200x200 rectangles wouldn't that TLE?
Hmm, I solved gold 2 by using stacks ad queue
My (bad) explanation for problem 2: so we have a vector of deques representing the current stacks of plates we also keep track of the maximum numbered plate that elsie has already washed and stacked when a plate comes to bessie: 1) if this plate has a number less than the maximum plate placed, there is no way that we can place this plate; output the current i 2) binary search for the stack whos bottom plate is as small as possible but greater than the target plate within the range of the 2 pointers (i.e upper_bound) 3) if all the plates in all the stacks are less than the target (this can be checked by looking at the bottom of the last stack), then create a new stack and move the second pointer forward 4) else if the target plate has label less than the top of the stack whos index we found during the binary search, then push the plate to the top of the stack 5) otherwise, move the first pointer to the index that we found with the binary search, and pop off all plates with numbers greater than the target plate (effectively we are getting rid of the plates that should come before the target). update the maximum plate to the tag of the last plate that we popped 6) push the target plate onto that stack 7) continue
I ended up using LCA+DFS Order+BIT for Gold #1...... am I crazy or was this an insane contest?
orz aryaman found it trivial
aryaman is a big orz
i second guessed myself too much whoops
orz arrayman
I do agree it was a pretty insane contest for gold ;-;
Testduk stop spamming or I'll reveal your main.
It felt insane, or at least very easy to overcomplicate and hence make insane.
My 7/10 for gold #2 was a decomposition into subsequences for each globally maximum element and then an O(n) amortised analysis to determine the first index which could not be cleaned, then the minimum of all these values is taken, which took like 3 hours ... :/
how much did you get in total
Nothing more. Had the idea for C but not enough time to implement in an hour. US open will be my last contest as a high schooler so hopefully it will go better :(
I did bin search on the index, then nlogn (sweep + binsearch) for nlog^2n sol which passed everything. It didn't take me that long. How did you do O(n) check?
Oops, I used a priority_queue; it was O(n log n) (I think)
How to solve Platinum 3? I thought of a segment tree to see the next coordinate I should move to, but this was wrong and ended up optimizing the O(N^2) DP with a set.
How many test cases did the optimization get?
silxi and I used the Segment Tree and Set optimizations to get 7-8 cases out of the 14 cases on that problem.
Same, I got 7/14 test cases
Ideas for plat P3 (I was out of time, so couldn't get AC with this. Feel free to point out errors):
We first precalculate the length of LIS ending at each point. With this information, we can easily have a naive n^2 DP solution: Let DP[i] be the smallest possible area, and do the transition for all pair that is a part of LIS.
To optimize this, we batch process all pairs i, j, such that DP[i] = x, DP[j] = x + 1, and (i, j) is "comparable" if Xi < Xj, Yi < Yj holds. Now, we do these three observation.
It seems we are almost done, but in reality, the "incomparable" pair gives a lot of trouble, and it would be impossible to build a divide and conquer based on this.
To overcome this, let's imagine a "magical segment tree", which will somehow respond to a range query asking for the minimum of DPi + (Xj - Xi)(Yj - Yi). Then, for each query, you will decompose it to intervals which belongs to a certain node in a segment tree. In the end, every node will receive a total of
intervals which belongs to a certain node in a segment tree. In the end, every node will receive a total of  queries which ask the minimum of DPi + (Xj - Xi)(Yj - Yi) in the interval represented by it.
queries which ask the minimum of DPi + (Xj - Xi)(Yj - Yi) in the interval represented by it.
You can notice, that every query point stacked in each node are comparable with all points in interval represented by its node. Thus, you can actually simulate that "magical segment tree" in an offline fashion, by collecting all points in each node and running divide-and-conquer optimization to solve the problem in each node. The time complexity is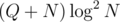 for each wave, and summing to
for each wave, and summing to 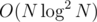 in total.
in total.
Although I introduced this solution as a "segment tree" approach, this is better to interpret as a divide-and-conquer solution. You don't actually need an explicit segment tree structures too: a divide-and-conquer which solves the "conquer step" with another divide-and-conquer will suffice. I believe the code will be actually quite pretty.
"If j1 < j2 in order of x coordinate, opt(j1) ≥ opt(j2) always hold, as otherwise we can swap them to obtain strictly smaller cost."
Can you explain how is this true? Unless I misunderstood your notations: j1, j2 is in the (x + 1)-wave and opt(j1), opt(j2) is in the x wave, right?
You are right, thanks for clarifying it.
For the proof, assume the contrary: j1 < j2, opt(j1) < opt(j2). Draw a trace of optimal solution that starts from j1 and j2. Between the x-wave and (x + 1)-wave, there exists two rectangles with intersection (cause they are comparable) and more following rectangles from opt(j1), opt(j2). Now swap opt(j1), opt(j2) and leave the following rectangles as is. The total area is strictly decreased, and you still have a valid solution. As we assumed both to be an optimal solution, this should not happen.
You mentioned 3D Convex Hull Trick. Do you know any place where I can learn about it?
Sorry, 3 years have been passed, and I still don't know how to do 3D CHT.
One of my friends came up with a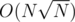 solution which is sufficient to get all the test cases. He used Divide and Conquer, but I'll present the solution without since his idea can easily be modified that way.
solution which is sufficient to get all the test cases. He used Divide and Conquer, but I'll present the solution without since his idea can easily be modified that way.
First, we partition the sequence into sets of elements with the same LIS value in increasing x-coordinate order (as usual). And we also do the DP where DP[i] = max(DP[j]+(x[i]-x[j])(y[i]-y[j])) where j ranges over all elements with LIS equal to LIS[i]-1 within the range of i (so it has to satisfy an increasing subsequence).
Let's ignore the condition for now that the chosen flowers have to form an increasing sequence, just that the LIS works (i.e. it goes from 0 to 1 to ... to max(LIS), hitting all consecutive numbers). Now, we claim that the best j to transition to goes in reverse order of x-coordinate as the x-coordinate increases within the same LIS value. You could prove this using simple inequalities, subtracting the differences for example.
Now, we break all elements with the same LIS into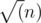 buckets. We still ignore the condition for now, and for each bucket we keep track of the best flower within that bucket to transition to given the current flower in the next LIS subsequence. To do this, we keep a "hull" set where for each adjacent flowers we can binary search when one passes another, and use this information to keep track of which flowers can ever be the transition (i.e. it passes the last flower at a point before the next flower passes this flower) and exactly at what point to switch to the next flower. This binary search takes
buckets. We still ignore the condition for now, and for each bucket we keep track of the best flower within that bucket to transition to given the current flower in the next LIS subsequence. To do this, we keep a "hull" set where for each adjacent flowers we can binary search when one passes another, and use this information to keep track of which flowers can ever be the transition (i.e. it passes the last flower at a point before the next flower passes this flower) and exactly at what point to switch to the next flower. This binary search takes 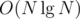 time. We store the points when to switch flowers so that when we compute the DP we know when to switch between current bests within each bucket. At most O(N) such points, so this switching part takes O(N) time.
time. We store the points when to switch flowers so that when we compute the DP we know when to switch between current bests within each bucket. At most O(N) such points, so this switching part takes O(N) time.
Now, we sweep across all flowers of the current LIS sequence which we want to compute the DP values of. Because the sequence of good transitional flowers form a consecutive interval as easily checked, note that at most 2 buckets partially intersect the sequence of possible transitions (the ones that satisfy the condition that it forms an increasing sequence), so we check all the values of the 2 buckets as possible transitions. For the rest of the buckets, if they don't intersect with the good interval at all we ignore it, otherwise they intersect entirely and we simply check the current best of the interval as a possible transition. You're checking at most values per transition, so the complexity is
values per transition, so the complexity is 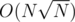 .
.
Thanks for sharing your solution. Could you elaborate the "hull" set thing when solving the problem for each bucket? Which criteria do you binary search upon, exactly?
I think this is kinda equivalent to my solution, just the matter of how to decompose the problem into "comparable" sets, and doing the transition efficiently without extra log factor.
The "hull" is not exactly a hull but it's mechanics is very similar.
Suppose you're transitioning from LIS = a to LIS = a+1, say stored in vectors v[a] and v[a+1] respectively.
Then, for each v[a][i] and v[a][i+1], you calculate the minimum value of j when v[a+1][j] would prefer to transition from v[a][i] than v[a][i+1] (ignoring the increasing condition for now).
Now, sometimes we have that v[a][i] exceeds v[a][i+1] before v[a][i+1] exceeds v[a][i+2], which in this case we delete v[a][i+1] from consideration as the transition state (and we repeatedly do this until we have a strictly decreasing state hull). We use pointers for the next element to transition to and store exactly when to transition.
Edit: I think this solution might be modifiable for a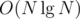 runtime. Instead of using sqrt(N) buckets, you use a tree-like structure and still make that calculation for each adjacent pair. The key is to note that between different segments you don't have to calculate the same pair twice, so you don't get an extra lg factor.
runtime. Instead of using sqrt(N) buckets, you use a tree-like structure and still make that calculation for each adjacent pair. The key is to note that between different segments you don't have to calculate the same pair twice, so you don't get an extra lg factor.
Thanks for the explanation. Combined with my solution, that will yield a solution.
solution.
How to solve p2? I wrote some "count the complement" dp at the last moment but it didn't work. And I think the complexity is like N^2 * Y or something, too slow.
Do you mean p2 of Platinum division? I also got a NY^2 solution, but with some optimization, the complexity can be reduced a little bit, so it can fit into the time limit.
If you want, I can try to elaborate my solution.
Please explain, thanks.
I've posted my solution here. The complexity is something like O(N2 + NY3 / 2).
I proved it earlier, and got the same complexity.
Edit: Oh, I think my complexity is a little bit worse than yours.
I'll first explain my O(NY2) solution, as it may be different from yours.
First, for each tree, I calculated number of paths in this tree that has distance d, for 0 ≤ d ≤ Y. for those paths with distance grater than Y are counted as d = Y. I also sum up distance for all paths with distance not less than Y.
This problem is asking for both picking routes in each tree and the order of them, but we need only the former part, as the later part can be done with a little bit math.
Let dpi, j = (count, sum) as number of ways to get total distance j (or Y, if the sum is grater than Y) from the first i trees, and the sum of distances.
To update the answer, I just enumerate each distance for the next tree, and update the appropriate values.
The dp array has complexity O(NY), and each update takes O(Y) time. So this approach took O(NY2) time in total.
I'll explain the optimization and the proves in the next comment, as I'm typing too slow...
We can see that when we got more trees, each individual tree are smaller, and their "distance => (count, sum)" array have many empty cells.
So I decided to "compress" them, that is to remove every empty cell. I put those non-empty cells into vector, so I can enumerate through each non-empty cells without taking time walking thorough empty cells.
Surprisingly, this approach indeed reduced time complexity down to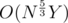 .
.
Let T be a positive number, using as a "threshold" size, we'll decide it's actual value later. Then we split those threes into two groups, one group with tree size less than T, and the other one with tree size grater than or equal to T.
Total complexity for the first group (smaller size) is O(T2NY), as each tree has at most O(T2) non-empty cell; Total complexity for the second group (larger size) is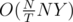 , as there could be at most
, as there could be at most 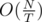 trees with size not smaller than T.
trees with size not smaller than T.
So the Total complexity is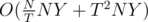 . Solving
. Solving 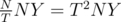 give us
give us 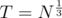 , which leads to total time complexity of
, which leads to total time complexity of 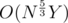
I think your time complexity is actually O(n*y*sqrt(y)).
Consider the trees with sizes s1, s2, .. < sqrt(y). There are s1^2+s2^2+.. < sqrt(y)(s1+s2+..) < O(n*sqrt(y)) total paths.
Consider the trees with sizes >= sqrt(y). Each tree has at most y different path lengths and there are at most n/sqrt(y) such trees, giving a total of O(n*sqrt(y)) paths.
Each update is O(y), so the total time complexity is O(n*y*sqrt(y)).
orz
I had an idea that also involved counting the complement, but I used generating functions and polynomial multiplication using FFT. Unfortunately I had a stupid overflow error during the actual contest, but I think this works.
I TLE'd with this approach (10 AC, 2 WA, 5 TLE). It's O(N^2+KYlogY) but I guess the constant factor dragged it down.
I had an O(N2 + CYlog(Y)) solution, where C = N - M is the number of connected components, which involves C fast polynomial multiplications. But when I submitted my "brute" solution using naive multiplication just to ensure correctness, it magically runs in 2.6 seconds :o So I didn't have to implement FFT. You can read my code here, it's quite easy to understand.
How to solve platinum p1?
Define ai as the probability of each cow not returning the invitation. Define the sequence bi as 1 / ai - 1. Consider an interval from indices l to r. Then the probability of exactly one cow returning the invitation is (bl + bl + 1 + ... + br) * (al * al + 1 * ... * ar).
Consider the interval obtained from extending the interval by one index to the right. We are interested in when (bl + bl + 1 + ... + br + br + 1) * (al * al + 1 * ... * ar * ar + 1) > (bl + bl + 1 + ... + br) * (al * al + 1 * ... * ar). You can cancel a ton, and eventually you get that this is equivalent to bl + bl + 1 + ... + br < 1.
Now, we can simply use two pointers with this condition, and compare the maximum intervals starting from each index. This gives an O(n) solution.
But what if adding the next element decreases the probability but adding the next two elements increases it? I submitted the same solution you described but it failed a few tests and I thought it's because this greedy is wrong.
This will never happen, because the sum of the b's always increases, meaning after it's no longer advantageous to add the next element to the chain starting from a certain index, it will never be advantageous to add more elements to the chain.
Why? If the sum of b is bigger then 1 we've only proved it's unadvantageos to add exactly one element.
Adding more elements will increase this sum, making it even more disadvantageous to continue adding elements.
Can anyone predict promotion cutoffs?
vamaddur and some other experienced people suggested that there would be a low cutoff (<700) for promotion from gold to plat. We'll get to know soon enough.
I was tagged here, so I guess I'll add my own two cents. :)
Gold P1 used a very similar idea to Promotion Counting, a relatively recent Plat problem, but the added twist of LCA has not been seen in divisions below Plat before AFAIK.
Gold P2 and P3 use relatively common Gold techniques (binary search and prefix sums, respectively), but P3 kinda looks like Fort Moo, but significantly harder.
I'm just going off the assumption that Gold division participants may not have been exposed to all these ideas yet until taking the contest, which would make the cutoff lower than normal (sub-700).
I think Gold P1 was significantly harder than Promotion Counting, as if I’m not mistaken range updates were required to solve it. (At any rate, I haven’t yet seen a solution without range updates that reaches O(Q log N).)
This was a very poor problem placement--the problem itself was fine, but it was too hard for Gold. The only reason this problem was close to gold-level is because it allowed the naive O(NQ) solution to pass, rewarding students who went for partial credit and penalizing those who spent their time working for a full solution.
There is a solution that uses a Fenwick Tree. I'm tagging the problem author if you want to hear all the solutions he's thought of :) peach
Are you referring to a Fenwick tree with only point updates? I’ve heard of some solutions using Fenwick trees with range updates and others that use Heavy-Light Decomposition; is there one you know of that works only with point-update BITs and LCA?
There is easy trick to do some "range update" on fenwick tree with just two point updates, so long as you only do point queries. We query value from root->node and then it is easy to cut out the intersection and account for LCA.
how would one think about problem 3? I was only able to get 4 cases as i simply printed out the value for the case when no new rectangles were added.
I was thinking about sliding window approach but then I only had 10 minutes left when I started #3
I think you mean gold P3? If so, 2D Kadane's algorithm and a line sweep while maintaining maximum subrectangle on both sides of the line should work (for right-left and up-down separately). Unfortunately my own implementation had a bug and I could only get 11/14 testcases but I verified the technique with at least one person who got a full solve.
What is 2D Kadane's algorithm? Does it calculate maximum weight subrectangle faster than O(n3)?
I learned it from https://stackoverflow.com/questions/19064133/understanding-kadanes-algorithm-for-2-d-array. It's just 1D Kadane's applied to a 2d matrix using prefix sums. I'm not aware of anything faster than O(n3), and O(n3) was more than sufficient for the problem since n = 200.
OK. My google scholar search also didn't found anything faster than O(n3 - ε) too.
was the contest rated?
When should one expect the cutoff score to be released?
Results and editorials are up at http://usaco.org/index.php?page=feb19results!
How to solve Gold #1?
I read the solution but i did not understand it.
Please help me to solve this problem.