gilcu3's blog

Probability theory
By gilcu3, 12 years ago, In English

I'm looking for a good source with deep theory and practice problems about probability, doesn't matter if it is too math involved, and I would prefer one that is ACM-ICPC training oriented.... thanks in advance..

  • Vote: I like it
  • +13
  • Vote: I do not like it

Comments Comments (9)
| Write comment?
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I need help too!! Anyone? Also need help on game theory.

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=probabilities

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    I've read that topcoder article already, but it doesn't seem to be enough, at least for solving problems where you must deal with expectations on random variables...

    → Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What would be necessary to learn to solve this problem? http://www.codechef.com/ACMAMR12/problems/MINMAX

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Nothing special , it just requires the basic definition of expected number and some about polynomial addition,multiplication and integration .

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How do you get the polynomials? I was able to doing only with two variables, by integrating over areas, but for more variables I didn't know what to do.

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I will try to explain my solution (though it seems more complex after I see others' solution.) Suppose you have to find the expected value of an expression ,say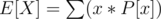
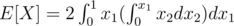
        M = Max(x1,x2)
        Then ,from the definition we have
        Assume M = x , then we have to find the probability that value of M is x.
        This will be when one of x1 OR x2 is equal to x , and the other has a value less than x. So

        Hence , E[X] = 2 / 3 .This was the case of simple two variables.

        Now come to the general case , we want the probability of the operator at the root , such that value after that is x .
        Consider this as a state F(node , {either 0,1,2}) , here 0 means that we have to find probability such that it has value equal to x , 1 means to find less than x , 2 means to find greater than x . Now our answer is (root,0) .
        The transition for example is like :
        Suppose expression is : MmxxMxx , then at the root we have Maximum(a,b) operator and we want prob for being equal ,so answer will be:

        (F(root->left,0)*F(root->right,1) + F(root->left,1)*F(root->right,0)) . Here F(node,{0,1,2}) will be a polynomial.

        This is because either left value will be equal to x or right , and in either cases the other one will have value less than x.

        For base case , if we have a leaf and we have to calculate F(leaf,0) then it is 1 , for F(leaf,1) it is x , for F(leaf,2) it is (1-x) .

        → Reply