dragoon's blog

GP of Bytedance 2018-2019
By dragoon, history, 6 years ago, In English

How to solve C, I?

  • Vote: I like it
  • +57
  • Vote: I do not like it

Comments Comments (28)
| Write comment?
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How to solve L?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    Instead of taking sum of 1 to 2. take sum for 1 to 2,3,4..,n . And then do ans/(n-1) at the end.

    Now since graph is connected assume you first build the bfs tree and then add extra edges. To do that do dp with states as number of vertices left and number of vertices in current level.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      I didnt think about "/(n-1)" part and made same solution without division, and wondered "why is MOD a prime number"

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Can you provide a bit more details? I see just an obvious way to do it in O(n4).

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +16 Vote: I do not like it

        Try build bfs tree from the farest blocks to the nearest.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Nice idea, thank you! Now I understand the whole solution :)

          → Reply
»
6 years ago, # |
  Vote: I like it +103 Vote: I do not like it

Samples to problem K are very nice!

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

I solved I with following idea:

Consider only central part of backet with width r: where centers of balls can be. Cut it by r from down and up. Now we have a box h - 2r by r, and the game is the following:

The first player chooses any point on bottom of the box (representing Center of first ball he chooses), after that player one by one choose points inside the box which lie higher than previous chosen point and which are at diatance exactly 2r from previous chosen point. One who can't choose a point inside a box looses

Now just simulate winning losing positions from the top to the bottom of the box. You will see they are periodic with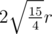 . It will be easy to see than that if integer part of is even than first player wins, otherwise second player wins

→ Reply
»
6 years ago, # |
  Vote: I like it +15 Vote: I do not like it

How to solve A?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    First, the vertices u and v are connected in the complete graph iff there is a path between them in the starting graph which contains only vertices with indices strictly less than min(u, v) (and u and v theirselves as its endpoints, of course).

    Second, let's find for each vertex i all possible pairs of vertices for which there is a path described above where i is the minimal vertex. It turns out that these endpoints are exactly i and every vertex with index  > i which is connected to any vertex v such that v is in the same connected component as i if we consider only vertices from 1 to i (that is, there must be a path between v and i over vertices  ≤ i).

    So if we denote such set for i by Si then it means that all vertices from Si must have different colors, and that means that the answer is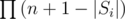 (because knowing this we can now paint vertices from n to 1 and each restriction gives us the corresponding number of ways to color each vertex). We can find out all these numbers building some DSU and adding all vertices from 1 to n there.

    I know this may be difficult to read, but I tried to write a brief scetch here, not a formal proof.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve G?

→ Reply
»
6 years ago, # |
← Rev. 5   Vote: I like it +20 Vote: I do not like it

C: first, I've implemented a simple solution that can only does bets of form for a fixed value of n, and made it print the optimal first bet for each starting amount of form . When I put n equal to a power of two, a pattern emerged. Here's an example for n = 16:

1 1
2 2
3 1
4 4
5 1
6 2
7 1
8 8
9 1
10 2
11 1
12 4
13 1
14 2
15 1

In other words, the optimal move for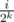 where i is odd is equal to .

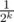It turned out that the optimal first move in this case does not depend on the value of p, and that the optimal first move is also the optimal move on subsequent steps, as no matter if we win or lose we get to a state which divides by a higher power of two and thus the next bet will be bigger as required by the problem.

Note that I don't have a proof, it's just what emerged from the above experiment.

In order to determine the probability of winning for a starting state that is not of the form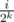 we will use the fact that the probability of winning is a continuous function. So we will represent the starting amount x is an infinite binary fraction x = 0.011100011010..., compute the probability of winning for each prefix of this fraction, and find the limit as the prefix goes to infinity.

We can compute the probability of winning for each prefix using the above observation and a relatively simple DP: if the prefix of length k is equal to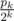 , then we'll compute the probability uk of winning if the starting amount is 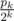and the probability vk of winning if the starting amount is .

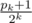The DP relation becomes: if pk is even (in other words, the k-th binary digit after the point is zero), then uk = uk - 1, and vk = p * vk - 1 + (1 - p) * uk - 1 (since if we have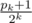 , out first bet will be 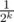). Similarly, if pk is odd, then vk = vk - 1, and uk = p * vk - 1 + (1 - p) * uk - 1.

Now we can quickly determine the probability of winning for any prefix of our infinite binary fraction. In order to find their limit we have to remember that the fraction is periodic, find the transformation that a whole period applies to uk and vk which ends up being something of form uk + m = α * ui + (1 - α) * vk, vk + m = β * ui + (1 - β) * vk, which means we're constantly chopping our segment by 1 - α on the left and by β on the right, so the limit divides our segment as 1 - α to β, in other words it is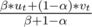 , where t is the length of the preperiod.

I won't be entirely surprised if this is equivalent to something much more straightforward :)

→ Reply
»
6 years ago, # |
← Rev. 5   Vote: I like it +105 Vote: I do not like it

Rick Astley — Never Gonna Give You Up.

The formal proof section of C is brutal. You've been warned. Petr s comment provides a more understandable albeit unproven method to solve the problem. The Handwaiving section describes some intuition behind the pattern. Also I'm a bit curious how many teams solved C by ignoring the nondecreasing part because they didn't like it and making the maximum possible bets because it seems logical to try end the game as fast as possible (and it is indeed correct if the nondecreasing restriction is dropped).

Bonuses: In some problems time limits were set to allow some solutions with unoptimal complexity to pass. It was done so for a reason because tighter TLs would lower the quality of those problems. The list of problems with their target complexities:

A: O(n a(n) + m), where a is the inverse Ackermann function. Basically the complexity should be dominated by a single pass over all edges with DSU.

B: O(n log n)

J: O(2^n m)

Finally I would like to apologize for unnecessarily tight time limit in L. Enforcing constant optimizations was not intended at all. Our two solutions worked for 0.2s and 0.5s and we didn't really find a way to make an even slower solution and thought that it should be ok.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

My bad, analysis already posted.

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

I have seeing these discussions of GPs for quite some time now, and I also want to participate. But idk any way to register on the cryptic site, or this one. This is highly off-topic for this post, but any help is appreciated. :)

→ Reply
»
2 years ago, # |
  Vote: I like it +71 Vote: I do not like it

How to solve G?

→ Reply