Не читайте, если вы ещё хотите написать тренировку.
Когда прочитал условие восьмой задачи, сразу подумал о динамике по поддеревьям.
Краткое условие: дано дерево из N вершин, необходимо найти кол-во способов выбрать 3 вершины так, чтобы попарные расстояния между ними были равны D.
Вот решение, это O(N), вся суть в dfs.
Подвесим дерево.
Для каждой пары (вершина X, число K) будем хранить такую информацию:
- количество потомков X на расстоянии K от неё.
- количество пар потомков X на расстоянии K от неё, LCP которых находится на расстоянии K - D / 2 от X.
Будем быстро получать эту информацию для очередной вершины по её детям. Окончательный ответ мы будем обновлять в процессе объединения результатов детей, поэтому самое важное — понять именно обновление и получение нужной информации.
В итоге для каждого поддерева будем хранить два вектора, отвечающих на те два вопроса. Длина каждого из векторов — это максимальный путь до листа в поддереве.
Чтобы получать нужную информацию через детей, научимся:
Добавлять ребро в начале поддерева. Понятно, что при этом в каждом векторе в начале появляется нолик. Но добавление в начало вектора — штука тормозная, поэтому вектора будем хранить перевёрнутыми, и добавлять нолики в конец.
Соединять два поддерева. Будем добавлять меньшее к большему. Это состоит из нескольких действий:
— Обновим ответ для случая, когда одна столица в одном поддереве, а две в другом. Перебираем расстояние до столиц в меньшем поддереве, умножаем соответствующие значения в векторах, добавляем в ответ.
— Обновим второй вектор для случая, когда в каждом поддереве по столице. Ясно, что тогда обе столицы на расстоянии D / 2 от данной вершины.
Кол-во способов это сделать мы легко получим произведением значений первых векторов у поддеревьев в позициях K = D / 2, а затем просто добавим во второй вектор нового поддерева в позицию, соответствующую K = 0.
— Обновим первый вектор. Если вершина одна, то она либо в первом, либо во втором поддереве, так что просто надо сложить первые вектора старых поддеревьев, чтобы получить первый вектор нового.
Всё.
Почему O(N)? Это просто.
Что мы делаем в процессе решения?
- Добавляем один элемент (нолик) O(N) раз суммарно
- Проходимся по меньшему вектору, обновляя ответ, меняя значения другого вектора, а затем удаляя каждый просмотренный элемент (все действия за O(1))
Больше мы ничего не делаем. А 2-ая операция не может удалить больше, чем сделала 1-ая.
Написание и отладка заняли 20 минут, зашло сразу.
Нельзя смотреть решения по нерешенным задачам (в тренировках).
Ваше объяснение как-то логически построено с конца, я вроде понял идею, но решение не осознал. Второй вектор — это все же количество пар на расстоянии K в разных поддеревьях? Почему тогда ответвления длины D/2?
Нет, на расстоянии K там та самая средняя точка, от неё дальше отходят ответвления на D/2.
UPD. выложил на pastebin
А, тогда ясно. Крутое решение, да.
Очень красивое и внятное решение.
Необычное такое применение меньшее-к-большему, которое обычно использовалось для получения асимптотик вроде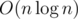
, а здесь для того, чтобы не добавлять новых элементов. Этот момент особенно понравился