Hi, all!
This year GP of China is scheduled on Sunday, March 10, 2019 at 11:00 (UTC+3). Writers have spent several days and nights creating and developing these problems. Hope you enjoy the contest!
UPD: Thanks to zimpha, Claris, quailty and me, here is editorial.
Links: OpenCup Main Page, GP of China (Div. 1), GP of China (Div. 2), and New Team Registration?











"The virtual contest is in progress. You are not allowed to participate" again...
It seems Div.1 is postponed for 2 minutes, and Div.2 will be postponed for 30 minutes.
UPD: Said on the main page, Div.2 will be postponed for 1 hour.
You shouldn't replace problems during the contest.
I finished coding some problem, tested samples, found that samples don't look correct, then reloaded the problem and found that the problem was changed to a completely different problem...
Maybe the old problem statement was misplaced by admin? I'm not sure about that. I have no access to the backend so far. Anyway, sorry for the inconvenience.
OK, sorry for complaining if it's not your mistake. I guess it's just an unfortunate error.
I'm just a contestant, can I register a sector?
I'm afraid I can't answer the question. If you really want to register, you can send messages to snarknews for more details.
What is test 44 in B?
k=1,2
Try this test:
1
6 6 1
2 4
1 6
6 4
2 5
3 6
5 4
Answer: Yes
Contrary to its outlook, J was actually very cool. Thanks!
C is pretty easy if we are given some oracle which draws a line slightly right to some two points, but it seems that's what actual problem is. Is there any easy way for that?
And how to solve H?
How to solve C if we can draw such line?
Assume n is even. Then we divide n points into half by sorting in pair (x, y) and draw some line almost parallel to x-axis. Now there is n / 2 points in each side. You pick convex hull of all points. Then there exists some edge in hull, which one point is in upper side, and other is in lower. Draw a line to eliminate it.
Of course this is not verified, so please tell me if this is wrong.
Here's an "oracle" that passes the tests:
It returns up to four segments, some of which pass slightly to the right, and others slightly to the left, so you try them all and take the one that eliminates the two points.
That's very clean, thanks!
How to solve J?
We first see how to enumerate all repeats in a string. Fix the length of repeat 2k. Divide the string into [0, k - 1], [k, 2k - 1].... We partition such N / k string into a maximal interval of string which all strings are same. Thus, we are left with some interval [ik, jk + k - 1]. If we slightly extend it right (by amount of LCP(ik, jk)) and extend it left (ReverseLCP(ik, jk)), they are the maximal substring which all 2k substrings are repeat. With suffix arrays we can enumerate them in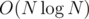 time.
time.
Thus, we are left with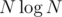 pieces of information indicating that there is an edge connecting x + i, y + i with cost w connecting
pieces of information indicating that there is an edge connecting x + i, y + i with cost w connecting 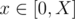 . Of course, we can decompose them in
. Of course, we can decompose them in  pieces where x = 2k for some k.
pieces where x = 2k for some k.
We will now process from k = 19 -> k = 0. Notice, that for each k, we only need O(n) such information. because anything that is not contained in spanning forest are useless. So, we can compress it by Kruskal's algorithm, and X information in k = t + 1 can be replaced with equivalent 2X information in k = t. If we propagate down until k = 0, we get exactly what we want. This gives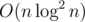 . While writing it down I found my implementation was actually
. While writing it down I found my implementation was actually 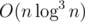 , but it passes in 1.5s so who cares.
, but it passes in 1.5s so who cares.
A piece can just be represented as two pieces where x = 2k since redundancy doesn't affect the answer.
The intended solution is to sort all k by wk and merge pieces found by length k.
We can maintain disjoint union sets for each k. When we want to merge x + i and y + i(0 ≤ i < 2k), first let's check whether x and y are already connected in dsuk, if so then we are done, just break it. Otherwise we need to connect x and y in dsuk and then recursively consider x, y and x + 2k - 1, y + 2k - 1 in dsuk - 1. Since there are at most O(n) times of merges in each dsu, the total complexity is
disjoint union sets for each k. When we want to merge x + i and y + i(0 ≤ i < 2k), first let's check whether x and y are already connected in dsuk, if so then we are done, just break it. Otherwise we need to connect x and y in dsuk and then recursively consider x, y and x + 2k - 1, y + 2k - 1 in dsuk - 1. Since there are at most O(n) times of merges in each dsu, the total complexity is 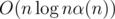 .
.
Yeah, it should be two pieces. I think that was my original thought, and I even preprocessed ⌊ log2(n)⌋ because of it. But somehow I did in the hard way :p
Is there a name for your method for enumerating repeats? I have seen it sevaral times, but cannot find any papers or blogs talking about it.
At that time I didn't know it's name. I just thought it was a well-known method. But I think people call it "Run enumeration" and there are more efficient method than what I've described.
Coincidentally, I'm writing a blog post about this, so you can learn about it soon.
A method related to Lyndon words for calculating runs is well- known in China, but I think this method is easier and more practical(in OI competitions we cannot use library). Maybe it should have a name.
I think the method based on Lyndon words are strictly better in terms of implementation and time complexity. The only downside is that it's hard to see the correctness (so people just have to memorize?)
I think I first saw this kind of problem on BOI 2004 Repeats.
Maybe your implementation of this method is too complex. You can see some implementations here. It's so simple after building a suffix array.
Maybe, but the linked problem is a simple one. Anyway, I wrote a blog post about it, though I think it's well known in China.
H:
Use centroid decomposion on T1. Suppose the centroid is o, and the distance between x and o is wx. What we need to calculate is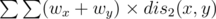 . Here x, y are vertices in a connected component S of T1 according to centroid decomposion.
. Here x, y are vertices in a connected component S of T1 according to centroid decomposion.
Let's take an edge with length len in T2. The contribution to answer is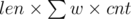 . It can be easily calculated using tree DP in O(n).
. It can be easily calculated using tree DP in O(n).
O(n) is too slow, but we can mark those vertices in S as important vertices. Let's compress those unimportant vertices whose degree is no more than 2, we will get a tree with O(|S|) vertices. Then run a linear tree DP on it is OK.
The total complexity is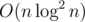 . The first
. The first
logis for centroid decomposion, and the secondlogis forstd::sortto build the compressed tree.The solution also exists, we leave it for readers.
solution also exists, we leave it for readers.
That's awesome... Thanks!
What is test 19 on B about?
k=3
We were failing test 19 because of this case:
1
4 4 1
1 2
2 3
3 1
1 4
Answer: No
I'm not really sure if this is test 19 or not (I can't pass it myself) but my solution fails miserably on a test like this and don't know now how to fix it yet)
Answer: No
How to solve D in O(n2) ? We managed to pass sample in O(n2 * log(n)), but unfortunately our solution is too slow.
My solution calculates expo(a, b) only when a, b ≤ n. Hence, powers can be precomputed.
Of course, we did it, but we had other difficulties. I will share our O(N2 * log(N)) approach. Let's calculate number of ways to make connected component with i vertices having cycle with j vertices on it. Let's call such value gi, j. Let's calculate fi and f2i using gi, j , total number of edges in all valid connected components with size i and total number of ways to build a valid component with i vertices, respectively. We calculated it in O(N2). Now let's dpi, j be the total number of edges in graph having i vertices and not having components with size greater than j. It's obvious that answer for N is dpN, N. And we don't know how to calculate dp with time faster than O(N2 * log(N)). The main idea we used to calculate dp is that we add components in non-descending order of their size. But since we can add more than one component of same size we should divide answer by cnt! and we can't just independently add two components of the same size. I mean we can't just calculate dpi, j as linear combination dpi, j - 1 and dpi - j, j. We should try every value of k and get the value of dpi, j as linear combination of dpi - k * j, j - 1.
How about only consider dpi, dp'i as the total number of edges in graphs having i vertices and the total number of graphs having i vertices? A typical approach is to enumerate the size k of the component which contains vertice 1 and regard the rest part as dp'i - k.
1) Precalculate xy for all x, y ≤ n. Also precalculate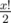 and
and  .
.
2) Calculate number of connected graphs with i vertices and a loop with length j — it's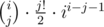 for 3 ≤ j ≤ i ≤ n and ii - 2 for j = 0 (with no loops).
for 3 ≤ j ≤ i ≤ n and ii - 2 for j = 0 (with no loops).
3) The resting part is quite straightforward. Calculate count of connected graphs with i vertices and no more than one loop, sum of edges in all loops in such graphs using values calculated in previous step. Let's say we calculated Ci and Si. Then we can calculate such values for all graphs (not only connected):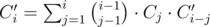 ,
, 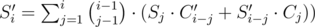
It was not hard for me to find a formula in part 2 because I've already seen similar formula. It was in TopCoder, SRM 700 Div1 Medium.
Thanks!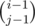 from the third part is exactly what we needed.
from the third part is exactly what we needed.
Great! The formula in part 2 is an application of generalized Cayley's formula, right? And seems like it appears in some Codeforces round.
Sadly I forgot to use that. Instead, I used the derivative of generating functions to get the conclusion. What a funny stupid :P
Yes, as TimonKnigge mentioned in a comment below it's just a generalization of Cayley's formula. By the way, I completely forgot about it too — I just remembered task with similar formula on TopCoder :)
Here is our solution, in quadratic time. We had to precompute exponentials to remove the logarithmic factor. I'm sure there's many ways to compute the answer though.
Let Cn be the number of partitions of {1, ..., n} into cycles. Take C0 = 1, then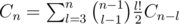 . Now note every partitioning will have n edges in a cycle.
. Now note every partitioning will have n edges in a cycle.
Let Hn count the number of partitions of {1, ..., n} into cycles with trees attached (so each component will have at least one cycle), weighted by the number of edges in cycles (per the problem statement. Then
Here we use a generalization of Cayley's formula. So $k$ is the number of vertices (and hence edges) in a cycle, and the remaining n - k vertices have to be attached as subtrees.
Finally, we may have some components that do not contain cycles. Let Wn count the number of ways to build such a forest with n vertices. Then W0 = 1 and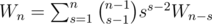 .
.
Finally, to compute the answer An we then have to partition the n vertices into components with and without cycles, so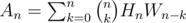 .
.
What's the easy way to code B?
To give up.
(Seriously, fuck that task.)
I don't think there's an easy solution, but here's what I did:
No.1component of size 3, 4, ..., k + 2. Those components should be cycles (number of internal edges = number of vertices). The other components should have size 1.Yes.Coding wasn't to bad, but figuring out all the cases was.
How to solve I?
We need to count number of equivalence classes of arrays of positive integers of length n with sum m and then subtract bad arrays that have some element at least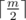 . Let's deal with bad arrays later. To count number of equivalence classes we use Burnside's lemma: it's equal to
. Let's deal with bad arrays later. To count number of equivalence classes we use Burnside's lemma: it's equal to 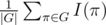 , where I(π) is the number of arrays that don't change after applying π and G is a group of permutations generated by a cyclic shift by one s and reversal r. Each permutation in G is either sk, i.e. a cyclic shift by k or skr, i.e. reversal followed by a cyclic shift by k, so |G| = 2n.
, where I(π) is the number of arrays that don't change after applying π and G is a group of permutations generated by a cyclic shift by one s and reversal r. Each permutation in G is either sk, i.e. a cyclic shift by k or skr, i.e. reversal followed by a cyclic shift by k, so |G| = 2n.
For sk, number of cycles is equal to gcd(k, n) and each cycle has length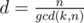 . On each cycle we need to have equal elements. So if elements of the i-th cycle are equal to ai, we have
. On each cycle we need to have equal elements. So if elements of the i-th cycle are equal to ai, we have 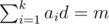 . If d doesn't divide m it's impossible, otherwise we need to count the number of sequences ai with sum
. If d doesn't divide m it's impossible, otherwise we need to count the number of sequences ai with sum 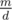 . It's a standard binomial coefficient problem. So far we learned how to do this part in O(n). But everything depends on gcd(k, n) and the number of k ≤ n such that gcd(k, n) = g equals to
. It's a standard binomial coefficient problem. So far we learned how to do this part in O(n). But everything depends on gcd(k, n) and the number of k ≤ n such that gcd(k, n) = g equals to 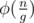 . So we can try all g dividing n and for each g multiply the answer by
. So we can try all g dividing n and for each g multiply the answer by 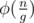 . We can precalculate φ(x) for all x ≤ 107 and after that this part of the solution will work in
. We can precalculate φ(x) for all x ≤ 107 and after that this part of the solution will work in  .
.
For skr, we notice that we have 0, 1 or 2 cycles of length 1, depending on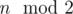 and
and 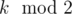 and all other cycles have length 2. If all cycles had length 2, we could again use binomial coefficients and everything would be easy. Notice that if we knew that some cycle of length 1 has even value, we could split it into 2 halves and treat it like a cycle of length 2. If it has odd value, we could subtract 1 and also split it into 2 cycles. So for each cycle of length 1 we try both cases. Here we need to be careful and remember which cycles can have zero values and which cycles cannot. This part works in O(1).
and all other cycles have length 2. If all cycles had length 2, we could again use binomial coefficients and everything would be easy. Notice that if we knew that some cycle of length 1 has even value, we could split it into 2 halves and treat it like a cycle of length 2. If it has odd value, we could subtract 1 and also split it into 2 cycles. So for each cycle of length 1 we try both cases. Here we need to be careful and remember which cycles can have zero values and which cycles cannot. This part works in O(1).
Now we need to subtract bad arrays. Notice that there can be only one edge with length at least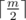 , so we cannot shift anything. But we still can reverse the array. So now we have |G| = 2 and we need to count the number of fixed points for id and r. id is obvious and r is very similar to the previous case: we have 1 or 2 cycles of length 1 and all other cycles have length 2. This is solved in the same way as previous case, except we subtract
, so we cannot shift anything. But we still can reverse the array. So now we have |G| = 2 and we need to count the number of fixed points for id and r. id is obvious and r is very similar to the previous case: we have 1 or 2 cycles of length 1 and all other cycles have length 2. This is solved in the same way as previous case, except we subtract 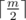 from one edge. Here's the code
from one edge. Here's the code
What's the point of constraints on modulo in D? Why 1 ≤ p?
Probably author wanted to increase amount of pain in this world
probably for the same reason we can have 2e5 tests with n=2e5, m=1 in B
The modulo had nothing to do with primes but it was somehow written as p
How to solve I?
How to solve F?
We tried some greedy after fixing permutation to kill monsters. After we kill first monster using 1...i, if we give it more damage than its health, we take some of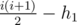 to give to other 2 players. These cannot be more than 102 each, so we brute over them. Also, these 2 damages cannot be same if they are ≤ 2. Then try to kill second monster using i + 1...j and possibly take some extra damage dealt during an intermediate attack to third monster similar to 1st case, but here all of this is transferred to third monster. Then we kill third as fast as possible. Can someone point out a flaw in this argument?
to give to other 2 players. These cannot be more than 102 each, so we brute over them. Also, these 2 damages cannot be same if they are ≤ 2. Then try to kill second monster using i + 1...j and possibly take some extra damage dealt during an intermediate attack to third monster similar to 1st case, but here all of this is transferred to third monster. Then we kill third as fast as possible. Can someone point out a flaw in this argument?
We may kill two little monsters first. In this case, the damages given to the boss monster may exceed 102, right?
In fact, we know in this case the first two monsters should be killed in no more than 102 seconds, since their health points don't exceed 100 and we only need to waste at most one second for the last monster.
P.S. Editorial is coming soon :)
Consider the example.
HPs: 1, 1, 1+2+...+1000
Attacks: 1, 1, 1e9
In this case it makes sense to kill the third monster in the first 1000 moves. If we delay his death and kill small monsters earlier, we get more damage from the large one (and fewer from the smaller ones, but that's minute).
So, in this example it is not true that small monsters die early. Am I wrong somewhere?
I would like to discuss the health points of the third monster first, and if HPC > 5050, I would discuss the order of their death. A mass of discussion, huh?
Probably I don't get your point. In the version of the analysis I have (shipped to the Moscow Workshop) there was a claim that the first two monsters always die in first 100 seconds. If I understand it wrong and some weaker statement is indeed claimed, I am happy to wait for the analysis with a proof.
It seems that the analysis was fixed last afternoon, so maybe what you've seen is an old version (and wrong). Please check out the final version that I posted on this blog.
The damage I am talking about( ≤ 102) is given to other monsters before the first monster dies completely. This will definitely be less that 102 if the monster 1 has low health. If monster 1 has high health, then it does not make sense to give more than 102 damage to other monsters while the high health monster dies, because they can die in weaker attacks.
This failed for test 3. Will it be possible to share the test cases?
If the high-health monster has health 1 + 2 + 3 + 4 + ... + 102 and does high damage too (say, 109), whereas the other two monsters have low damage (say, 1), then you should still attack the high-health monster first.
From round 100 (or rather, max{Ha, Hb}) you can speed this process up though by binary searching for when monster c is dead, after which you can one-hit the other one or two monsters that remain.
Try this one:
1
6 3 6 5 3 5
Answer: 54
F:
Auto comment: topic has been updated by skywalkert (previous revision, new revision, compare).