Div II A — Завидный забор

Задача

Нужно определить, существует ли правильный многоугольник, углы которого равны a.

Решение

Рассмотрим все смежные углы правильного n-многоугольника с углом a, они равны 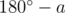. Их сумма равна 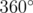, так как многоугольник выпуклый. Тогда выполняется следующее равенство: n·(180 - a) = 360, которое означает, что ответ есть, когда .

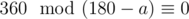Время: O(t).

Память: O(1).

Реализация: C++, Java

Комментарий

Задача также решается поворачиванием вектора (1, 0) на угол величины 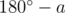, пока он не вернётся на свою позицию (поворот делаем не более 360 раз), и проверяя, совершили ли мы ровно один полный оборот (пример реализации: C++).

Это также одна из редких задач на Codeforces, у которой всего 1 пример, 1 претест и 1 полный тест.

Div II B — Обсуждения

Задача

В этой задаче просилось найти количество элементов n-перетановки, которые обязательно должны были быть перемещены после выполнения нескольких движение-к-началу операций. Альтернативно, мы должны найти максимальное количество элементов, которые могли быть не затронуты.

Решение

Если какой-то a_i больше, чем a_i + 1, то ясно, что a_i точно был перемещён, так как порядок этих двух элементов изменился. Пусть последний такой элемент является a_k. Тогда все элементы a_k + 1, a_k + 2, ..., a_n могли быть не затронуты операциями, так как их порядок не изменился. Ответ на задачу равен n - k. Если такого a_k нет, то порядок не изменился вообще и тогда могло не быть операций.

Время: O(n).

Память: O(n) / O(1).

Реализация: C++, Java

Комментарий

Задача появилась, когда автор зависал на главной странице Codeforces, пытаясь придумать лёгкую задачу для Div II. =)

Div II C / Div I A — Волшебные ларцы

Задача

Нам даны a_i квадратов со стороной 2^k_i. Квадрат разрешено поместить только в больший квадрат, при том никакие два квадрата не дожны перекрываться. Мы должны найти наименьшее p такое, что мы можем поместить все данные квадраты в квадрат со стороной 2^p.

Решение

Допустим, что мы можем поместить все квадраты внутри квадрата со стороной 2^p. Тогда можно разместить квадраты типа k_i независимо друг от друга по сетке так, как показано на рисунке. Никакие два квадрата не будут перекрываться, так как 2^x делит 2^y, если x < y. Это значит, что мы можем найти наименьший квадрат, который вмещает все данные квадраты со стороной 2^k_i для каждого k_i отдельно. Тогда ответ будет равняться стороне наибольшего такого квадрата.

Чтобы можно было разместить a_i квадратов со стороной 2^k_i внутри квадрата со стороной 2^s, должно выполнятся следующее равенство:

Тогда мы можем найти наменьшее s:

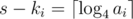
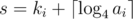
В частном случае, когда s = k_i, s увеличиваем на 1.

Время: .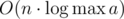

Память: O(1).

Реализация: C++, Java

Комментарий

Задачу также можно решить двоичным поиском по p. Однако, заметим что каждый квадрат со стороной 2^k + 15 помещяет в себе любое данное количество квадратов со стороной, меньшей 2^k, так как 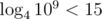. Поэтому достаточно найти первый подходящий квадрат со стороной от 2^{max k + 1} до 2^{max k + 15}.

Div II D / Div I B — Теплица

Задача

На прямой даны n точек, каждая одного типа от 1 до m. Мы можем раздеить прямую на m - 1 интервалов и переместить какое-то количество точек так, чтобы каждая точка типа i находилась бы внутри i-того интервала, которые пронумерованы от 1 до m слева направо. Нужно найти минимальное количество точек, которые нужно переместить.

Решение

Сперва заметим, что данные координаты не нужны: важен только порядок точек. Пусть мы можем переместить какое-то количество точек, чтобы получить годную перестановку. Тогда все остальные точки остались на своих местах, поэтому их типы должны неубывать слева направо. Поэтому достаточно найти наибольшее количество точек, которые могут остаться на своих местах, что является наибольшей неубывающей последовательностью типов среди данных типов. Если эта длина l, то ответ n - l.

В этой задаче достаточно было реализовать квадратичное решение. Считаем dp[i][j] — длина наидлиннейшей неубывающей последовательности на префиксе [1;i], где j — тип последнего элемента. Переход динамики:

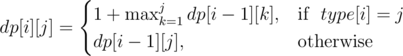
Для лёгкой реализации, хватает завести один массив dp[j], и пропустить обработку второго случая.

Время: O(n²) / .

Память: O(n²) / O(n).

Реализация: C++

Комментарий

С этой задачей мы столкнулись во время работы над проектов, и суть проблемы лежит в размещении границ некоторых прямоугольных таблиц. Наша оригинальная реализация работает за O(nm).

Div II E / Div I C — Неисправный Поток

Задача

В этой задаче нам дан неориентированный граф и поток по нему, и требуется найти направление этого потока на каждом ребре.

Решение

Ключевой элемент к решению задачи — следующее наблюдение: если нам известны все входящие рёбра одной вершины, то остальные рёбра должны быть исходящими. Исток не имеет входящих рёбер, поэтому мы уже знаем, что все его рёбра исходящие. Для всех остальных вершин, исключая сток, количество входящего и исходящего потока одно и то же, и равняется половине суммы потока, проходящего по всем рёбрам из этой вершины. Тогда алгоритм заключается в многократном направлении всех рёбер из вершин, для которых все входящие рёбра уже известны. Это можно сделать одним BFS:

for all v from 2 to n-1
    f[v] := sum(flow(v,u))/2;
put source in queue
while queue is not empty
    v := pop(queue)
    for all edges (v, u)
        if (v, u) is not directed yet
            direct v -> u
            f[u] = f[u] - flow(v,u)
            if u not sink and f[u] = 0
                push(queue, u)

Так как поток не содержит циклов, вершины можно упорядочить топологически. Поэтому мы можем быть уверены в том, что пока все рёбра не направлены, мы можем положить в очередь по крайней мере ещё одну вершину с некоторыми ещё ненаправленными рёбрами, так как все вершины, из которых в неё входит поток, находятся перед ней в топологическом порядке.

Время: O(n + m)

Память: O(n + m)

Реализация: C++, Java

Комментарий

Очевидное «простое» решение — запустить алгоритм нахождения максимального потока на том же графе, и получить ответ. Однако все такие решения сваливались на претесте #6.

269D - Максимальный водопад

Задача

Нам даны n горизонтальных отрезков, а также 2 дополнительных, самый верхний и самый нижний. Эти два отрезка являются истоком и стоком потока. Поток может течь с одного отрезка на нижний отрезок, если их горизонтальные проекции перекрываются, а также между ними нет другого такого отрезка, что их проекции перекрываются. Количество потока по таком ребру равняется длине перекрытия проекций. Нужно найти наибольшее возможное значение потока, который может течь по какому-то пути из отрезков.

Решение

Для решения задачи используем метод сканирующей прямой. Эта горизонтальная сканирующая двигается снизу наверх и содержит все части отрезков, которые видны с этой прямой в данной позиции. Каждая часть также содержит ссылку на свой изначальный отрезок. Сама сканирующая реализована балансированным двоичным деревом поиска.

События сканирующей являются отрезками. Когда встречается новый отрезок, мы хотим найти все такие нижние отрезки, на которые мы можем направить поток с этого отрезка. Такими могут быть только такие отрезки, чьи части находятся в сканирующей и перекрываются с данным отрезком. Затем мы итерируемся по всем таким частям p (найти первую такую часть — операция). Как мы узнаем, можно ли направить поток на p? Заметим, что если какой-то другой отрезок мешает этому, то в сканирующей должна существовать такая его часть q, которая видна с данного отрезка. А так как все три проекции этих отрезков перекрываются, то такая часть может быть только сразу слева или справа от p в двоичном дереве. Поэтому мы просто проверяем, не мешают ли изначальные отрезки таких двух частей рядом с p направить поток с данного отрезка на на изначальный отрезок p.

Затем мы вынимаем все такие части из сканирующей, и кладём новую часть, соответствующую данному отрезку. Если этот отрезок только частично перекрывал какую-то из частей в сканирующей, мы вставляем обратно остальную часть этой же самой части. Таких частей может быть только две — по одной на каждой стороне отрезка. Поэтому при обработке каждого отрезка вставляется не более 3 новых частей и размер сканирующей O(n). Каждая часть обрабатывается ровно один раз перед выниманием, поэтому суммарное время таких операций .

Когда мы узнаём, что можно направить поток по , сразу же обновляем наибольший возможный нисходящий поток из a:

Когда обработаем верхний отрезок, f_top будет ответом.

Время:

Память: O(n)

Реализация: C++, Java

Комментарий

Ещё одна задача из нашего проекта. Также можно явно построить граф, используя отрезки, используя такую же сканирующую прямую, и только после найти путь наибольшего потока в этом графе. В оригинальной постановке нужно было найти этот граф, без верхнего и нижнего отрезков.

Div I E — Теория Струн

Задача

В этой задаче нам дан прямоугольник n × m. Каждая серединная точка едичного отрезка на сторонах соединена с другой точкой на другой стороне прямоугольника. Разрешено менять порядок рядов и столбцов, но отрезки должны оставаться прикреплёнными к своим точкам. Нужно найти такую перестановку рядов и столбцов, что никакие два отрезка не пересекаются, или же определить, что таковой не существует.

Решение

Всего есть 6 разных типов отрезков, соединяющих стороны:

1. слева-наверх;
2. сверху-направо;
3. справа-вниз;
4. снизу-налево;
5. слева-направо;
6. сверху-вниз;

Если есть и слева-направо, и сверху-вниз отрезки, решения не существует. В противном случае остаются только пять типов отрезков. Без потери общности допустим, что нет именно слева-направо отрезков. Взглянем на то, как должен выглядеть прямоугольник после перестановок:

Все справа-вверх отрезки должны находится в левом верхнем углу, и соединять точки (L,i) и (T,i), иначе они бы точно пересекались с какими-нибудь отрезками. Аналогично должны быть расположены все сверху-направо, справа-вниз, снизу-налево отрезки. Все сверху-вниз отрезки же должны быть параллельными. Также заметим, что количество слева-наверх отрезков должно быть равно количеству отрезков справа-вниз, а количество сверху-направо отрезков должно быть равно количеству отрезков снизу-налево. Из этого следует важное наблюдение: картинка прямоугольника после перестановок задана однозначно и может быть получена из входных данных, просто считая количество отрезков каждого типа.

Далее мы определяем понятие цикла: это последовательность отрезков, где вторая точка каждого отрезка равняется первой точке следующего отрезка на противоположной стороне прямоугольника. В данном примере всего два таких цикла (но направления циклов важно):

Заметим, что множество циклов не меняется при любой перестановке по определению цикла. Теперь мы знаем набросок решения: нужно найти все такие циклы в данном прямоугольнике и в конечном прямоугольнике, и сравнить их на равенство.

В данный момент мы действительно находим циклы в обоих прямоугольниках. Есть только два типа циклов:

1. (слева-наверх) (сверху-направо) (справа-вниз) (снизу-налево);
2. остальные циклы

Можно легко проверить, равняются ли между собой множества циклов первого вида, так как длина таких циклов 4. Если они совпадают, то мы переставляем соответствующие ряды и столбцы в правильном порядке.

Как сравнить остальные циклы? Рассмотрим следующий пример:

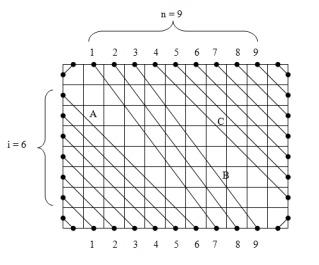
Пусть разница количеств слева-наверх и слева-вниз отрезков равна i, а это число плюс количество сверху-вниз отрезков равно s. Если пронумеровать точки, как показано на рисунке, можно заметить, что кажая точка k сверху соединена с нижней точкой 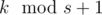(сверху-направо отрезки продолжаются как соответствующие слева-вниз отрезки). Это можно описать перестановкой

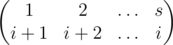
Наши циклы соответствуют циклам перестановки, при том сверху-направо отрезки продолжаются в слева-вниз именно там, где в этой перестановке элемент цикла уменьшается. Известно, что перестановка такого типа состоит из 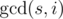циклов длины 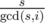, то есть все циклы одинаковой длины. Обозначим каждый тип отрезка одним символом (на рисунке A, B, C). Тогда не только длина, но и строки, соответствующие циклам, тоже равны, но могут быть циклически сдвинуты, когда мы их нашли (именно здесь важно направление циклов). Кроме того, мы уже знаем, как выглядит такая строка из конечного прямоугольника. Поэтому нам нужно сравнить строки всех оставшихся циклов из данного прямоугольника с этой строкой, беря во внимание сдвиги как инвариант. Для каждой строки это можно сделать за линейное время, например, с помощью алгоритма Кнута-Морриса-Пратта. Когда для каждого цикла находим значение циклического сдвига, перестанавливаем ряды и столбцы по соответствию с конечным прямоугольником.

Время: O(n + m).

Память: O(n + m).

Реализация: C++, Java

Комментарий

По части реализации это настоящий гроб. Для нас ушло 5 часов, чтобы каждому написать решение. Ещё раз поздравления kelvin, в момент написания разбора единственному участнику, решившему эту задачу (и конечно же любому, кто сдаст эту сложную задачу в дорешке =) ).