Maintain subtree information using link/cut trees

#	User	Rating
1	tourist	4009
2	jiangly	3831
3	Radewoosh	3646
4	jqdai0815	3620
4	Benq	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	gamegame	3386
10	ksun48	3373

#	User	Contrib.
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	160
5	-is-this-fft-	158
6	awoo	157
7	adamant	156
8	TheScrasse	154
8	nor	154
10	Dominater069	153

In the tutorial of 1172E - Nauuo and ODT, I didn't write things on how to maintain subtree information, because I thought it was a popular trick. However, through tmwilliamlin168's comment, I realized that this trick may be not so common in other countries, so I decided to write a blog on it.

This blog will tell you how to maintain subtree information using LCT, with solutions on some problems, so you should know LCT before reading this blog.

Main Idea

The main idea is simple: record the sum of information of "virtual subtrees", where the "virtual subtrees" refers to the subtrees except the one in the Splay.

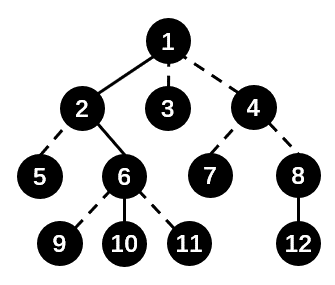
In the picture, $$$1$$$, $$$2$$$, $$$6$$$, $$$10$$$ are in a Splay, while $$$8$$$ and $$$12$$$ are in another. The "virtual subtrees" of $$$1$$$ is $$$3$$$ and $$$4$$$, the "virtual subtrees" of $$$4$$$ is $$$7$$$ and $$$8$$$, the node $$$8$$$ has no "virtual subtree".

You need to update the information when the "virtual subtrees" changes, usually, when accessing and linking.

An easy example is using LCT to maintain the size of subtrees.

Here are some codes:

struct Node
{
    int fa, ch[2], siz, vir; // father, two children, size of subtrees (including the root), size of virtual subtrees
} t[N];

void access(int x)
{
    for (int y = 0; x; x = t[y = x].fa)
    {
        Splay(x);
        t[x].vir -= t[y].siz; // update the size of virtual subtrees
        t[x].vir += t[t[x].ch[1]].siz;
        t[x].ch[1] = y;
        pushup(x); // update the information of the node x
    }
}

void link(int x, int y)
{
    makeroot(x);
    access(y);
    Splay(y);
    t[x].fa = y;
    t[y].vir += t[x].siz;
}

void pushup(int x)
{
    t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].vir + 1;
}

Problems

Some problems are in Chinese, I will translate the statements (in a simplified version).

[BJOI2014] Great Integration

There are initially $$$n$$$ nodes, there will be $$$q$$$ operations in two types:

A x y add an edge between $$$x$$$ and $$$y$$$
Q x y a query, asking how many simple paths are there which go through the edge between $$$x$$$ and $$$y$$$.

It is guaranteed that the graph is always a forest (one or more trees).

Input

n m
m lines of operations

Tutorial

Solution

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 100010;

struct Node
{
    int ch[2], fa, vir, siz;
    bool rev;
} t[N];

bool nroot(int x);
void rotate(int x);
void Splay(int x);
void access(int x);
void makeroot(int x);
void split(int x, int y);
void link(int x, int y);
void reverse(int x);
void pushup(int x);
void pushdown(int x);

int n, q, sta[N], top;

int main()
{
    int x, y;
    char op[10];

    scanf("%d%d", &n, &q);

    while (q--)
    {
        scanf("%s%d%d", op, &x, &y);
        if (op[0] == 'A') link(x, y);
        else
        {
            split(x, y);
            printf("%lld\n", 1ll * (t[x].vir + 1) * (t[y].vir + 1));
        }
    }

    return 0;
}

bool nroot(int x) { return x == t[t[x].fa].ch[0] || x == t[t[x].fa].ch[1]; }

void rotate(int x)
{
    int y = t[x].fa;
    int z = t[y].fa;
    int k = x == t[y].ch[1];
    if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
    t[x].fa = z;
    t[y].ch[k] = t[x].ch[k ^ 1];
    t[t[x].ch[k ^ 1]].fa = y;
    t[x].ch[k ^ 1] = y;
    t[y].fa = x;
    pushup(y);
    pushup(x);
}

void Splay(int x)
{
    int u = x;
    sta[++top] = x;
    while (nroot(u)) sta[++top] = u = t[u].fa;
    while (top) pushdown(sta[top--]);
    while (nroot(x))
    {
        int y = t[x].fa;
        int z = t[y].fa;
        if (nroot(y)) (x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? rotate(x) : rotate(y);
        rotate(x);
    }
}

void access(int x)
{
    for (int y = 0; x; x = t[y = x].fa)
    {
        Splay(x);
        t[x].vir += t[t[x].ch[1]].siz;
        t[x].ch[1] = y;
        t[x].vir -= t[t[x].ch[1]].siz;
        pushup(x);
    }
}

void makeroot(int x)
{
    access(x);
    Splay(x);
    reverse(x);
}

void split(int x, int y)
{
    makeroot(x);
    access(y);
    Splay(y);
}

void link(int x, int y)
{
    makeroot(x);
    access(y);
    Splay(y);
    t[x].fa = y;
    t[y].vir += t[x].siz;
}

void reverse(int x)
{
    swap(t[x].ch[0], t[x].ch[1]);
    t[x].rev ^= 1;
}

void pushup(int x)
{
    t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].vir + 1;
}

void pushdown(int x)
{
    if (t[x].rev)
    {
        reverse(t[x].ch[0]);
        reverse(t[x].ch[1]);
        t[x].rev = false;
    }
}

UOJ #207. Gongjia toured Changsha

There is a tree consisting of $$$n$$$ nodes and a multiset of simple paths $$$S$$$. $$$S$$$ is initially empty. There are $$$m$$$ operations in $$$4$$$ types:

x y u v $$$cut(x, y)$$$, $$$link(u, v)$$$
x y insert the simple path $$$(x, y)$$$ in $$$S$$$
x delete the $$$x$$$-th simple path inserted in $$$S$$$
x y a query, asking if all simple paths in $$$S$$$ go through the edge $$$(x,y)$$$

It is guaranteed that the graph is always a tree.

Input

the id of subtask
n m
n-1 lines of the initial tree
m lines of operations

Tutorial

Solution

#include <algorithm>
#include <cctype>
#include <cstdio>
#include <ctime>
#include <iostream>

using namespace std;

int read()
{
    int out = 0;
    char c;
    while (!isdigit(c = getchar()));
    for (; isdigit(c); c = getchar()) out = out * 10 + c - '0';
    return out;
}

typedef unsigned long long ull;

const int N = 100010;
const int M = 300010;

ull seed = time(0);
ull rd() { return seed = seed * 998244353 + 1000000007; }

struct Node
{
    int ch[2], fa;
    ull self, val, vir;
    bool rev;
} t[N];

bool nroot(int x);
void rotate(int x);
void Splay(int x);
void access(int x);
void makeroot(int x);
void link(int x, int y);
void cut(int x, int y);
void reverse(int x);
void pushup(int x);
void pushdown(int x);

int id, n, m, sta[N], top, sx[M], sy[M], stot;
ull xorp[M], xorsum;

int main()
{
    int i, x, y;

    id = read();
    n = read();
    m = read();

    for (i = 1; i < n; ++i) link(read(), read());

    while (m--)
    {
        switch (read())
        {
            case 1:
                cut(read(), read());
                link(read(), read());
                break;
            case 2:
                sx[++stot] = x = read();
                sy[stot] = y = read();
                xorp[stot] = rd();
                access(x);
                Splay(x);
                t[x].self ^= xorp[stot];
                access(y);
                Splay(y);
                t[y].self ^= xorp[stot];
                xorsum ^= xorp[stot];
                break;
            case 3:
                x = read();
                access(sx[x]);
                Splay(sx[x]);
                t[sx[x]].self ^= xorp[x];
                access(sy[x]);
                Splay(sy[x]);
                t[sy[x]].self ^= xorp[x];
                xorsum ^= xorp[x];
                break;
            case 4:
                x = read();
                y = read();
                makeroot(x);
                access(y);
                if ((t[y].vir ^ t[y].self) == xorsum) puts("YES");
                else puts("NO");
                break;
        }
    }

    return 0;
}

bool nroot(int x) { return x == t[t[x].fa].ch[0] || x == t[t[x].fa].ch[1]; }

void rotate(int x)
{
    int y = t[x].fa;
    int z = t[y].fa;
    int k = x == t[y].ch[1];
    if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
    t[x].fa = z;
    t[y].ch[k] = t[x].ch[k ^ 1];
    t[t[x].ch[k ^ 1]].fa = y;
    t[x].ch[k ^ 1] = y;
    t[y].fa = x;
    pushup(y);
    pushup(x);
}

void Splay(int x)
{
    int u = x;
    sta[++top] = u;
    while (nroot(u)) sta[++top] = u = t[u].fa;
    while (top) pushdown(sta[top--]);
    while (nroot(x))
    {
        int y = t[x].fa;
        int z = t[y].fa;
        if (nroot(y)) (x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? rotate(x) : rotate(y);
        rotate(x);
    }
}

void access(int x)
{
    for (int y = 0; x; x = t[y = x].fa)
    {
        Splay(x);
        t[x].vir ^= t[t[x].ch[1]].val;
        t[x].vir ^= t[t[x].ch[1] = y].val;
        pushup(x);
    }
}

void makeroot(int x)
{
    access(x);
    Splay(x);
    reverse(x);
}

void link(int x, int y)
{
    makeroot(x);
    access(y);
    Splay(y);
    t[x].fa = y;
    t[y].vir ^= t[x].val;
}

void cut(int x, int y)
{
    makeroot(x);
    access(y);
    Splay(y);
    t[x].fa = t[y].ch[0] = 0;
    pushup(y);
}

void reverse(int x)
{
    swap(t[x].ch[0], t[x].ch[1]);
    t[x].rev ^= 1;
}

void pushup(int x)
{
    t[x].val = t[x].self ^ t[x].vir ^ t[t[x].ch[0]].val ^ t[t[x].ch[1]].val;
}

void pushdown(int x)
{
    if (t[x].rev)
    {
        reverse(t[x].ch[0]);
        reverse(t[x].ch[1]);
        t[x].rev = false;
    }
}

1172E - Nauuo and ODT

You can see the problem on Codeforces, and the tutorial is also available here.

Comments (6)

Write comment?

Chilli

5 years ago, # |

← Rev. 3 →

Is it possible to both support path queries between u and v as well as subtree queries? My understanding is that to support path queries, one typically roots the "real" tree at u or v, and then can access the path query along the "aux/virtual" tree from the root to v.

However, that fundamentally changes the structure of the "real" tree, right? Isn't that incompatible with subtree queries? I could imagine one could do it if you implemented path queries with LCA or something like that, but I haven't seen anybody do so.

Notation: "aux/virtual" tree = tree represented by splay "real" tree = your underlying tree being represented.

→ Reply

RobeZH

4 years ago, # |

I believe the link function in your example code should have a "access(y);splay(y)" just like in your code for "[BJOI2014] Great Integration"?

ouuan

4 years ago, # ^ |

+23

Added now.

SecondThread

Can this be adapted to maintain aggregate subtree values for things that you can't 'remove' from? Like subtree max, for instance?

+10

Yes. You can change the variable vir from an integer to a multiset, and change the corresponding function.

Okay, I think I see. And then if you needed something like GCD, you could make it a treap and recalculate the answer in log(n) time each remove. I suppose it adds a log factor to everything, but it works. Thanks!