Только что закончился очередной Гран-При, предлагаю здесь обсудить задачи.
Расскажите, пожалуйста, решение A, F, G.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:04:37
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:04:37
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 10:30:23 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
Хотелось бы также узнать решения задач L, R, S из див.2.
L — dp[mask][it] — делаем много итераций (имитируя бесконечность), переходы очевидны, те состояния, в которых mask заканчивается на первую строку прибавляем к ответу.
вроде можно такие вещи честно решать, составлением графа переходов (вершины будут mask).
R — прсото перебор, поддерживаем массив use — какие числа уже были, ответ находится быстро.
S — dp[mask1][mask2] — максимальный средний выигрыш — mask — карты, которые на руках 1го и 2го соответсвенно, переход такой — ходим какой-то картой, суммируем все исходы по любой карте второго, учитывая, что все ходы второго равновероятны, среди всех ходов 1го выбираем максимум
Вопрос по L. Я честно говоря не понял, почему мы вообще можем считать вероятность выпадения той или иной строки раньше. Ведь мы бросаем "идеальную" монетку и любые последовательности у нас выпадут с одинаковой вероятностью, или я чего-то не понял в условии?
Вопрос по R. Не понятно как находить ответ и числа у нас же могут быть длиной до 1000, как их хранить?
по R. если b = 1, то ответ 0, иначе n <= 13. нам даже не важно n, т.к. все числа у нас не превосходят b^n<=10000, т.к. такой вектор из n элементов, это ни что иное, как запись числа в b-ичной системе счисления
Так, с количеством чисел теперь понятно, нужно было внимательнее смотреть на ограничения. А как их теперь склеить в одну строку, чтобы каждое встречалось только 1 раз?
В R на самом деле надо искать эйлеров цикл на графе, вершины которого являются наборами размера n со значениями от 0 до b — 1 (ну и понятно с какими рёбрами). Но там граф настолько специфический, что проходит и просто "дописывать всегда самое большое возможное число в конец".
да, точно, что-то я совсем забыл про эйлеров цикл
G — паросочетанием просто: в каждой доли числа от a до b, ребро проводим если их сумма является квадратом.
F — противная задача, мы разбирали разные случае в зависимости от знаков. Общая идея такая: до lcm(a, b) — влоб считаем, после lcm(a, b) идут с периодом gcd(a, b).
G: нам еще потребовалось сделать жадное приближение, чтобы осталось не больше сотни свободных вершин. Приближение было такое: перебираем числа с больших к меньшим, находим минимальное число, которое в сумме даёт квадрат и жадно берём все числа между ними.
А можете код показать? На таком решении получили TL 96.
Наше такое тоже давало ТЛ 96. Побороли так: сначала делаем Куна, только в ДФС спускаемся не больше чем на 5, такая жадная инициализация. А потом обычный Кун.
Есть простой хак с Куном, который часто помогает: В дфсе пытаемся первым проходом поставить в ребро в ещё не взятую вершину правой доли, а если не получилось, пробуем найти увеличивающую цепь.
Код: http://pastie.org/private/i7ovmcte5bn6pkipw84ug
F на самом деле ничуть не противная. Если a*b < 0 — то в ответ попадают все числа которые делятся на gcd. Иначе пусть для определенности a, b >= 0 (в обратном случае просто домножим на -1 все входные данные). Пусть b > a(опять-таки если это не так посвапаем их), составим граф остатков по модулю b, ребрами этого графа будет понятно что — переходы между остатками, получаемые применением операций +a и +b. Заметим, что операция +b переводит остаток сам в себя, поэтому, получив один раз данный остаток по модулю b, мы его умеем получать каждый раз. Таким образом, для каждого остатка найдем. когда мы впервые его получили, далее для числа R переберем все остатки по модулю b и, зная, когда этот остаток в первый раз встретился, легко найдем сколько раз этот остаток встретился от 0 до R. Дальнейшее тривиально.
Серег ты наверное хотел сказать gcd а не lcm
Да, спасибо
A — мега-баян, там явная формула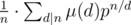
. Ну и побороться с непростотой m, посчитав по модулю nm.
G — строим граф и втупую ищем паросочетание, прокатывает.
А кто-нибудь пробовал делать I? У нас там 2^16 раз решается поиск равновесия по Нэшу на матрице 8x8, и мы это делаем симплекс-методом, что конечно же не прокатывает. Кто-нибудь знает нормальный способ искать равновесие по Нэшу?
У Рената такое же решение, неясно, почему бы не прокатить? Там вроде 2562·8·(симплекс-метод на 8 переменных, 17 ограничений)
Ну потому что симплекс-метод фиг знает за сколько работает. У нас ещё какой-то неправильный симплекс-метод был, падало на assert'е, что задача ограничена (на 7ом тесте, который, похоже, первый макстест).
Re к следующему комментарию: а почему верхняя и нижняя цены могут не совпадать? Казалось бы, тут самый обычный Нэш.
Вроде бы, симплексс-метод всегда работает как раз быстро, он работает долго только если не повезет. Но, возможно, авторы сделали хорошие тесты и надо было писать эллипсоиды.
Да ладно, ну в такой игре сложно сделать что-то "плохое" все матрицы вполне хорошие задачи специфичные(матричные игры) и тп.
Я не умею доказывать, что такого сделать нельзя. В любом случае, авторы могли бы и поподробнее условия написать. Потому что кто их знает, что они под минимаксом понимают. Выяснится потом, что задача была совсем другая.
Только там не Нэш, а минимакс, Нэша может и не быть, т.к. нижняя и верхняя цены игры могут не совпадать
Имеется ввиду Нэш в смешанных стратегиях.
Дело в том, что согласно условию имеется ввиду как раз минимакс. Т.е. не факт, что выигрыш в каком-то из смешанных равновесий Нэша будет для первого игрока таким же большим, как и минимаксимальный.
Если надо было искать именно смешанное равновесие (и оно почему-то одно?), то задача проще, и вроде бы не нужен симплекс-метод.
Я всегда думал, что симплекс метод нужен именно для смешанных стратегий... равновесие в смысле значения одно, а вот в смысле стратегий конечно не единственное
не понял, а почему значение должно быть одно во всех равновесиях? Равновесие Нэша в некотором смысле локальное понятие.
Я продолжаю говорить про смешанные стратегии. Например потому что множество оптимальных стратегий 1 и 2 игрока это прямоугольник.
Я тоже говорю про смешанные стратегии. И все равно не понимаю вас. О каком прямоугольнике идет речь? В этой задаче пространчтво стратегий каждого из игроков 8мерное.
Ну вообще у нас есть теорема о минимаксе из линейного программирования. Для матричной игры из неё следует, что выйгрыш первого и второго совпадают(Из-за того что задача линейного программирования для второго это двойственная к задаче лп первого). Если мы вдруг найдём точку равновесия по нэшу и значение в ней будет не совпадать с с нашим минимаксным значением, то мы в зависимости от того меньше оно или больше можем подвинуть стратегия первого или второго до оптимальной, что идёт в противоречее тому, что это равновесие.
Вы, кажется, немного путаететесь. Теорема о минимаксе говорит, что в равновесии Нэша минимакс и максимин равны. Но из этого не следует все, что вы пишете.
В задаче нас просят найти минимакс (так написано, хотя конечно авторы могли иметь ввиду что угодно). Если бы просили найти максимин, равный при этом минимаксу, то да, это точно было бы равновесие Нэша. Но тут вроде бы такого не требуют
Цитата из википедии ни о каком равновесии нэша речи не идёт. The minimax theorem states[1] For every two-person, zero-sum game with finitely many strategies, there exists a value V and a mixed strategy for each player, such that (a) Given player 2's strategy, the best payoff possible for player 1 is V, and (b) Given player 1's strategy, the best payoff possible for player 2 is −V.
Иными словами есть смешанное равновесие Нэша и в нем минимакс и максимин свопадают. То, что это равновесие Нэша в вашей цитате не написано, но это так (можете проверить). Но из существования не следует единственность
И кроме того, в любом случае неясно, почему вы думаете, что в задаче надо найти именно это? Вроде бы в условии написано, что ищется минимакс (ни слова про максимин нету)
Пусть мы нашли (xa, ya) и есть вторая точка равновесия (x0, y0) . Пусть H(xa, ya) > H(x0, y0) тогда H(xa, y0) > = H(xa, ya) > H(x0, y0) следовательно H(xa, y0) > H(x0, y0) значит (x0, y0) не равновесие. Аналогично со знаком в другую сторону. Значит значение во всех ситуациях равновесия одинаковое.
Да, вы правы, в треде ниже мы пришли к тому же выводу =) остается лишь убедиться, авторы действительно имели ввиду равновесие Нэша и решить задачу без симплекс-метода.
А как искать именно смешанное равновесие без симплекс-метода? Мы именно равновесие искали, и это успешно дошло до 7 теста безо всяких WA.
Тут важно, гарантируется ли, что оно одно. Потому что иначе неясно, какое значение выбирать
1) А можно ли пример, когда в игре с нулевой суммой есть несколько равновесий по Нэшу (отличающихся по среднему исходу) в смешанных стратегиях? 2) Можно ли пример, когда в игре с нулевой суммой минимакс по смешанным стратегиям отличается от равновесия по Нэшу в смешанных стратегиях?
1) Нужно взять блочно-диагональную матрицу с разными равновесиями в каждой из подматриц. UPD. Это неверно, тоже думааю. 2) думаю
Про блочно-диагональную всё-равно не понимаю. С такой матрицей вроде всё в порядке:
Я уже написал, что про блочно-диагональную неверно
Упс, доказал, что 1) не бывает. Доказательство довольно легко строится от противного.
UPD. Упс, доказал, что 2) не бывает. Доказательство почти такое же.
Почему WA 14 в A? использую вышеупомянутую формулу
А как вы по модулю m на n делите?
Матрица всего один раз 8x8, в остальных случаях меньше :) Так что думаю должно прокатить. Мы не смогли симплекс-метод написать тоже.
За симплекс-метод страшно, там надо лексикографическое уточнение писать.
Мы собирались устроить приближенное решение, но время закончилось.
А как именно получать ответ в конце, если делать по модулю m * n?
просто поделить на n
А почему так можно делать?
потому что число (длинное) обязано делиться на N нацело, значит и по модулю N*k тоже будет делиться на N нацело
Т.е. получается мы умеем делить по любому модулю?
Если на константу — то да. Ну или на что-то с не очень большим НОКом.
Интересно. Я правильно понимаю, что в общем случае так не сделать? Ну т.е. есть способ факторизовать модуль и решать отдельно для piαi, но он не работает если надо складывать/вычитать.
Всё так. Например, после деления у нас делится модуль. А еще мы принципиально пользуемся тем, что исходное число делится нацело (хотя в противном случае непонятно, что такое "деление по модулю", если не взаимно просто с модулем).
как решать B див1?
Первая идея: решить систему линейных уравнений с около 50 * 50 переменными. Состояние — какой префикс у первого, какой у второго. Все переходы предподсчитываем. Решать такую систему долго, поэтому приходим к идее, что состояний на самом деле около 2 * 50. Состояние определяется как номер игрока с большим префиксом и длиной префикса. Длина меньшего префикса после этого определяется одназначно. Составляем систему и решаем.
А какую систему составляем? Можно поподробнее?
Есть 2 * 50 переменных — вероятность выиграть первого игра в соответствующем состоянии. Состояние — размер наибольшего из префиксов обоих игроков и номер игрока, у которого такой префикс. Максимальный суффикс этого префикса, подходящий другому игроку, будет его префиксом. Если в состоянии конец игры — присваиваем явно соответствующей переменной 0 или 1. Иначе, из каждого состояния есть 2 перехода, отсюда получаем уравнение вида f(x) = (f(go[x][0]) + f(go[x][1])) / 2.
Ой. Действительно всё просто. А я матрицу в степень возводил...
Так же надежнее, все числа положительные нет страха нарваться на потерю точности в гауссе.
... что не помешало мне несколько раз получить по этой задаче WA44 до того, как я заменил double на long double.
А как можно понять условие Е? Мы час пытались распарсить его, но ответ на второй сэмпл выносит мозг... Вот ИТМО 1 что-то даже пытались посылать)
Не проверял по тесту, но по-видимому видимому правила такие: 1) Муж фиксирует смешанную стратегию и сообщает её жене 2) Жена выбирает, где отвлекать мужа 3) Муж выбирает чистую стратегию согласно смешанной, и действует исходя из неё, при этом жене не сообщает
нет, вроде бы он просто выбирает смешанную стратегию, такую, чтобы получить наибольшее матожидание в худшем случае.
А он знает, когда его жена отвлекат? То есть, он предполгает, что мог проехать поворот, а мог не проехать?
не знает. Стратегию он выбирает еще до поездки. И на каждом повороте, который он заметил, он знает какой это поворот по счету (не вообще, а среди замечнных) и с какой вероятностью ему сворачивать.
Ну это то же самое т.к. это игра с нулевой суммой. Кстати говоря, мою клару по поводу того, когда жена выбирает стратегию, жюри так и не прочитало.
А, я понял, что ты имел ввиду под выбирает чистую стратегию. Тут есть только нюанс, связанный с тем, что если жена k поворотов напропускает, то последние k стратегий мужа сольются в одну, ведущую в конец главной дороги.
Я все понимаю, контесты бывают не новые, но чтобы две задачи были на тренировках, которые давал я — это перебор.
Причем одну из них потом не взяли на CF по причине конвергенции мыслей с opencup.
Что ж это не помогло вам всех порвать? :) < /trololo>
А какие именно задачи?
Мы новообразованная команда, еще не сыгрались :)
Задача B с точностью до у меня был лимит 500 и H с точностью до у меня был перечислен список тех, кто должен присутствовать.
Все еще в мою бытность студентом.
И ещё расскажите D и H, пожалуйста.
H можно решать так. Построим граф. Вершины — слова длиной (n — 1). Дуги — буквы. Дуга A соединяет вершины (u, v), если после преписыванием буквы A к слову u, последние (n — 1) буквы (u + A) дают v. Эйлеров цикл в этом графе даст решение. Но можно проще. Пусть сначало слово 00...0. Достаточно каждый раз приписывать самую большую букву, чтобы получившееся при этом слово нигде еще не встречалось. Для этого можно для каждого хэша слова длины (n — 1) помнить, что писали в прошлый раз, и выводить это значение минус 1.
D. Пока что только идеи, для второго дива достаточно. MAX ищется просто, каждый раз берёшь первый и последний город. Это легко доказать. Похожий подход для MIN — берешь K пар соседних городов. Это делается динамикой N x K.
Если кто-нибудь может рассказать D, расскажите пожалуйста.
Задачу D для минимума можно переформулировать так: дано n чисел, надо выбрать k из них так, чтобы никакие два выбранных не лежали рядом; при этом хочется максимизировать их сумму. Zhukov_Dmitry предлагает следующее решение: делаем k шагов, на каждом количество выбранных отрезков увеличиваем на 1, причем делаем это "жадно", т.е. выбираем наиболее сильно улучшающий нас вариант из всех валидных вариантов вида "... 0 1 0 1 0 ... 0 1 0 ..." -> "... 1 0 1 0 1 ... 1 0 1 ..." (1 — взяли, 0 — нет). Искомые цепочки и их прирост Zhukov_Dmitry, как я понял, хранил с помощью сета и, видимо, хипа. Почему сие работает — неизвестно, но аналогично решалась недавно бывшая где-то задача вида "из n чисел надо выбрать не более чем k подотрезков с наибольшей суммой"...
Почему это работает можно понять так. Отсортируем все города. Построим двудольный граф, в одну долю отнесем города, которые находятся на нечетных позициях после сортировки, в другой — на четных. Проведем между соседними городами ребра с весом, равным расстоянию между ними. Тогда понятно, что нам нужно набрать паросочетание размера К с минимальным весом. Если решать эту задачу минкостом, то можно заметить, что на каждой итерации, когда пропускаем еще одну единицу потока, мы находим как раз такую цепочку, которая наименьшим образом увеличивает наш ответ.
Спасибо огромное, сие действительно работает)))
Просто надо сформулировать эту задачу в терминах потока минвеса (разбив точки на 2 доли по чётности), а потом заметить, что жадное приращение на 1 — это фактически поиск дополняющего пути минимального веса. Update: Мда, нужно привыкнуть обновлять страницу перед тем как писать ответ.
И все равно огромное спасибо)))
У кого-нибудь при отправке в дорешивание решение на Java (javac-32) появляется "Ошибка проверяющей системы"?
Исправлено. Сейчас javac-32 работает и в дорешивании (проблема была в разных language id на разных экземплярах системы)
Задача T из Div 2, Не могу найти ошибку (WA 20). Mожет алгоритм неверный ? код.
begin
read(fin,n); q:=n; for i:=1 to n do begin read(fin,s);
if s=0 then begin write(fout,n-i+1/q); q:=q-1; end;
if s=1 then write(fout,1/q); end;end. this is algorithm :)
Can you explain how it works ?
yes if there is 0 the chance that he sits in his place is (n-i+1) mans that left div q(q is the number of chairs,q is changing ,because if there is 0 than 1 place is alread taken so q:=q-1;) if 1 than man can sit in any place so 1/q. :)
Где можно почитать эти задачи?
После окончания подведения итогов гран-при их выкладывают на opencup.ru.
Ссылка на условия I дивизиона.