Hello!
International Olympiad in Informatics (IOI), the most prestigious programming contest in the world, is held in a beautiful city of Baku, Azerbaijan this year.
Wish the best luck to every contestant!
Day1: The contest had started on time, but the scoreboard is broken. It seems there is no mirror this year.
Day1 Contest Overview: Benq solved all Day1 problems in only 3.5 hours, congratulations! Full scorers for each tasks: 23(rect) / 170(shoes) / 6(split)
Day2 Contest Overview: The winner for Day2 is duality, but Benq still secures his consecutive IOI win. Congratulations! Full scorers for each tasks: 0(line) / 47(vision) / 2(walk)
Contest Results
- Benq 547.09
- 300iq 511.22
- duality 494.33
- TLE 491.46
- FizzyDavid 482.39
Country Ranking
- 1 Russia 4G
- 2 China 3G1S
- 2 United States of America 3G1S
- 4 Republic of Korea 2G1S1B
- 4 Vietnam 2G1S1B
Congratulations to everyone who competed, and especially to our super awesome team gina0605 GyojunYoun Onjo blackbori !
Useful Links:











The scoreboard is no longer broken!
And Korea first place in 1hr! (GyojunYoun)
How do you know that?
Also, I see you downloaded the task statements, how did you do that? I can't find anything on the IOI site.
He has access to the tasks because he is a leader for team Korea.
It's just a guess :p
I downloaded it last night because I was helping the translation.
Abridged statements:
shoes: You are given $$$2N$$$ nonzero but possibly negative integers. You should minimally swap adjacent pairs to achieve:
for all $$$0 \le i < N$$$. What is the minimum required swaps? It's guaranteed that it's possible. $$$N \le 100000$$$
split: Given undirected connected graph $$$G$$$. find a tripartition of $$$V(G)$$$ of size $$$a, b, c$$$ respectively ($$$a, b, c$$$ given in input), where at least two of the partition is “connected” (it’s induced subgraph is connected). Return the tripartition or state that it's impossible. Note that it's partition, so $$$a+b+c=n$$$. $$$|V(G)| \le 100000$$$
rect: You are given a map of $$$N \times M$$$ grid where each cell has integer height $$$0 \le H[i][j] \le 7000000$$$. A rectangle is a set of rectangular area $$$[x1, x2] \times [y1, y2]$$$ s.t $$$1 \le x_1 \le x_2 \le N-2, 1 \le y_1 \le y_2 \le M - 2$$$ (so should NOT contain cells in edges). A rectangle is valid if for each cell $$$(i, j)$$$ in rectangle, $$$min(H[x1-1][j], H[x2+1][j], H[i][y1-1], H[i][y2+1]) > H[i][j]$$$ holds. Count the number of possible rects. $$$N, M \le 2500$$$.
What's the constraint of $$$N$$$ in problem `shoes'?
$$$N \le 100000$$$
Change "7M" to normal number, it's confusing.
done
Also, shoes are identical to this task, but IOI has higher limits (editorial tells how to solve higher limits anyway).
This issue was raised in the GA meeting but was rejected.
I don't like it too, but apparently, ISC didn't found the better task, so maybe it's better than yet another Nowruz.
Ask me next time, I have a couple of good tasks prepared.
You can ask them in Call for Tasks
After reading this comment I want to downvote somebody, but I know that it isn't your fault. :/
Good that there are some other comments which deserve downvotes xd
Well, if you need to downvote someone to make yourself feel better, feel free to downvote me. I was one of the delegation leaders who voted to keep the problem, and for me this was a conscious decision after thinking about the proposed problem (with the subtasks it had and everything) and feeling that the problem was different enough. The post by eduardische below shows that your "identical to" was far from being correct.
I guess the problem you (and on other occasions, many other strong contestants) have is that you are only evaluating the problem from your own point of view. Sure, to you as a contestant the problem may look identical, but that's just because you are too good and you don't realize the difficulty the additional steps bring.
In this particular problem, the Codeforces version is just the old "when you are arranging stuff by swapping adjacent elements, don't make unnecessary swaps". I assume that nobody who solved it in the contest spent any time to think about the faster solution, and I'm convinced nobody tried to implement it. And you are also being unfair when you claim that the editorial tells you how to solve the IOI problem. It doesn't. It's just a single sentence that tells you that you have to use an efficient data structure. Well, if you are an average IOI participant, that part is already obvious from the constraints. But while to you it may also be obvious how to use it, it definitely was not obvious to every participant. Plus, the IOI problem brings a bunch of new stuff you have to deal with: What if the leftmost shoe is a right shoe? How exactly should I handle multiple shoes of the same size (both in the idea and in the implementation)? All of these questions are suitable challenges for someone who aims for bronze.
From where I'm sitting, the IOI problem is a nice generalization of the CF problem. Solving the CF problem helps a bit, but so does solving any other problem about swaps of adjacent elements, because the only thing it actually gives you is intuition on the greedy strategy. There is enough new that is neither in the CF problem, nor explained by the note in its editorial.
Problems that are both easy enough and significantly more original than this one are incredibly rare.
How can someone be too good for IOI?
The editorial mentions the following:
Add "in case of tie pick leftmost", then you get 85 points. So until 85 points, it's an identical problem.
I think your typical argument of "you are a soulless red coder but purples will agree" is nonsense. You are just avoiding criticism. “Pick leftmost" strategy is clearly doable if you studied hard enough to remember that CF one. I was blue 5 yrs ago, and I also hold contests for blue. Don't dismiss them, or us.
Agreed, but this is IOI, so they are usually one of the best problems in the world. Problems such as 2015 boxes, 2018 combo are easy enough but much more innovative.
I haven't been involved in selecting the problems for this IOI in any way other than raising my country sign along with 70+ other people, so at least in this context "avoiding criticism" makes no sense to me -- I'm not the one being criticized when people dislike that this problem was used. I'm just trying to explain why I personally find the problem OK. Or more precisely: not great, not terrible.
I don't understand the obsession with originality at all costs -- given that it's hardly possible nowadays, and it can only get worse. E.g., I also love the task Boxes, but I can easily show you older problems that are easier versions of it in the same sense in which the CF task was an easier version of the IOI task this year. There are literally hundreds of thousands of problems out there, and if you dig enough, you'll find something that uses the same idea -- especially if that idea is easier. Most of the easy IOI problems are similar to other problems that have appeared before. IMHO, on its own this should not be perceived as a bad thing.
At the IMO it's common that problems 1 and 4 can be solved using standard techniques, and everybody expects that the well-prepared contestants will easily, quickly and consistently solve them, as they would have seen and solved ten similar problems before. The problems 1 and 4 are there to challenge the lower part of the field, not the crowd fighting for gold.
The IOI needs to do the same. In order to be as fair as possible when handing out the medals in the end, the problem set cannot be top-heavy only. If you do that, you would have a clear winner and random noise in the middle of the ranklist. The problem set needs to have parts that discriminate well around each of the medal boundaries. If you are really lucky, someone will contribute an easy ad-hoc problem, but in past years that happened only rarely and going forward such problems will only be more rare. Most of the easy IOI problems will have to look like this one: be based on clever use and modification of standard techniques. This is precisely the type of problems for which everyone who (to use your words) "studied hard enough" will have already seen the technique and they just have to apply it to solve the problem. In my point of view, this is precisely what was going on in the Shoes problem. In particular, I'm convinced that the CF problem gave less advantage to people who solved it than e.g. any of the many problems in which you move stuff to the left of an array and use a Fenwick tree to keep track of it. That implementation is much closer to what they had to write here.
I don't agree to your opinion about IMO. It's true that well-prepared contestants solve problems 1 and 4 easily, but I don't think it's because they have seen ten similar problems. At least, I always expected to see problems easily solved but with new or uncommon ideas.
Nevertheless, it's hard to find an easy, interesting and new problem, so you may not be able to put one in IOI. Only in such a case should tasks like shoes (easy and interesting but not new) be used.
But actually, in this year's IMO, problems 1 and 4 are very typical and everyone who studied hard enough must have already seen the technique and they just have to apply it to solve the problems. So, organizers, including leaders, probably think in the similar way.
Re IMO, I think I have similar expectations as you but I use different words to describe them. I do expect those problems to be uncommon in the sense that I would not have seen that exact problem before, I just expect them to be standard in the sense that I would have seen and used the techniques that work on them before. Or, more precisely, what usually makes these problems easy to me is that the techniques you'll try intuitively will work, and gaining that intuition is precisely thanks to the practice we put in. E.g., you read 2018-4, you see that it's about chess knights, you remember problems about placing many knights onto a chessboard and related invariants, and you apply those to this problem.
I guess another part of the problem is that originality is not binary -- problem isn't just "original" or "not original", it's (at least) somewhere on a real-valued scale and different people with different experience will necessarily place it on different places on that scale.
I agree with everyone that problems that fall on the "more original" end of the spectrum for most people are the best. I would love to have such IOI and IMO problems every year, I just don't expect that we can realistically have that, and I'm saying that the second best is still not a tragedy if we don't.
:) Haha you reminded me of this problem I wrote for an ACM contest that was identical to 2015 Boxes. It didn't cause big problems though, as that contest was only one week before IOI2015, and only one China team member had seen this problem beforehand
Seems like "another Nowruz" happened anyways.
Today's task is way harder.
I think it's OK because that problem has the correct solution. I believe the data was given as output-only because it was very tricky, and there is a benefit of giving input data with visualizers.
Wow, ksun48's only CF task ever can make IOI???
So identical that everyone who solved it on CF got easy 100 points.
I didn't get 100 points lmao
There was a major objection on this task that it was too similar to the task on CF with only restriction bump (but the editorial discussed the faster solution) and the unimportant complications; and the argumentation was that around 40 IOI contestants competed in that round.
ISC recommended that since it believes there are enough differences between the tasks, it was designed to be the easiest task of the set, and the backup option wasn't recommended as viable by ISC; to keep the task as is. There also was a precedent for the situation back in 2016, when the task found to be close to the one used in ICPC contest was kept, partially because it was also designed to be easiest in the set, although to be fair, that task was from way earlier contest 10 years ago at the time. This objection was voted down by 58 to 4 votes with 3 abstentions to keep the task in, which later was claimed by the delegation who lodged the complaint to be simply because many countries have already started translating the task and didn't want to translate another task, which I personally find very arrogant and disrespectful towards other delegations.
At the end of contest, I found 13 people who solved the task on Codeforces but didn't get 100 points for it, which in my eyes show that the ISC recommendation was well intended and that the task wasn't that identical to the one on Codeforces.
While I agree that you have some valid points, "very arrogant and disrespectful" perfectly fits you, who namechecked all 13 people without 100 points.
I'm going to assume that by "namechecked" you meant "named", as I did check the entire table from the mapping to CF handles, and I fail to see how analysing publicly available data is arrogant or disrespectful. I'm assuming number 40 yesterday also didn't come up from the thin air.
However, I agree that it was not the right decision to implicitly name the 13 people I found as the backup for the data and I apologize for that if it caused any offence. Simple aggregation would have been enough, so I concede to your description in this instance.
I was one of those 13 people, I dont feel offensed. Also something to consider is, its an older contest, I didnt even remember solving this problem. I didn't even remember it existed. It was 14 months ago
Hey, i am it :)
39613311 didn't get 100 pts?
To give more data to people who are not in the GA meeting, ISC also pointed out the fact that at least 3 of the ISC/HSC (I forgot who is the other one, sorry) solved the problem during the contest (in $$$O(N^2)$$$) and did not realize about it when reading the task.
To me, the greedy intuition is "just another simple greedy intuition" that we can easily forget after solving the Codeforces task. Even if contestants do remember, there are still the additional steps to solve the problem. As demonstrated by eduardische above, some contestants did forget about the problem, or did not manage to solve the additional steps.
In problem "split", it isn't always possible is it? Do we have to determine whether it is possible as well?
Consider a star. Also, consider this sentence: "Return the tripartition or state that it's impossible."
Oh, the sentence was not there when I commented, thank you for pointing out :)
Wow, you're right, sorry then :)
It was done by myself before your comment, so somehow you got the older revision? Thanks for the clarification anyway.
A "state that it's impossible" phrase isn't really a guarantee that the task really is impossible; it might be just a trick of the setters. But I agree, the star case is enough to show impossibility.
Do you think that IOI is prestigier than ICPC?
Obviously
Somewhy I think opposite :)
The tasks for #ioi2019 first competition day:
http://jonathanirvin.gs/files/ioi2019/
Scoreboard mirror by snarknews.
Problem split reminds me this theorem (Can be spoiler): Link to arXiv
Can someone verify?
Without loss of generality, we can assume that a <= b <= c, and we want to find connected components of size a and b, then all the remaining vertices go to the third part.
Let's solve the tree subtask first. Root in the centroid. Let's consider centroid's sons and sizes of their components ($$$a_1$$$, $$$a_2$$$, ..., $$$a_k$$$) respectively. Each of those does not exceed $$$n/2$$$. Clearly, if none of those components has size >= a, it's impossible to find the desired partition. Otherwise, we can just take that component, find first partition there, and find the second partition in the rest of the graph (there are definitely enough vertices there).
Back to the general case. We can pick any spanning tree and solve the problem as if it was a tree problem. If we failed to find a solution, it means that every component has size smaller than a. We will now consider connections between the components and build a new graph consisting of those $$$k$$$ vertices, where each node has some weight $$$a_i$$$, and connections to other components according to the previously ignored non-tree edges. We aim to find a connected part of size at least a in the new graph, and break the DFS as soon as we manage that (!).
If we fail, then it must have been impossible to find the desired tripartition. Otherwise, we can take that component, find a vertices there and other part of the graph will definitely have a connected component of size at least b. Why? The overhead in finding part $$$a$$$ is at most $$$a-1$$$, because otherwise we would have stopped the DFS earlier. Since all the components are connected through the centroid and $$$a <= b <= c$$$, it means that there are at least $$$b$$$ nodes in the rest of the graph.
Thus, we get a very implementable solution. Shoutout for problem setter!
That's exactly the same as what I did :)
Task split is in my opinion completely amazing, easily best problem of the year so far!
Taking c to be the biggest and having required 2a+b<=n as a consequence which is needed in the process of the solution just plays out in such a satisfying way!
Even though I solved the task, I have no idea what you're saying here...
Lemma: assume the graph is biconnected and let $$$x, y$$$ be such that $$$x + y = n$$$. Then there exists a partition of the graph into two connected subgraphs of sizes $$$x$$$ and $$$y$$$.
Proof: find any st-ordering of the vertices of the graph, which can be done in $$$O(m+n)$$$ or $$$O(m \log n)$$$ time. Then, take its prefix of length $$$x$$$ and suffix of length $$$y$$$ as the subgraphs. From the definition of an st-ordering, it's easy to see that they are connected. (end)
Lemma 2: assume the graph is biconnected, but now the vertices have positive weights not exceeding $$$w$$$. Then, if $$$x, y$$$ are such that $$$w + x + y \ge n$$$, then there exists a partition of the graph into two connected subgraphs of total weights at least $$$x$$$ and $$$y$$$.
Proof: find any st-ordering as above. Find the shortest prefix of the ordering with weight $$$\ge x$$$. Its weight will be less than $$$w + x$$$, so the corresponding suffix has weight $$$\ge y$$$. (end)
Now, let's $$$a \le b \le c$$$. Consider the block-cut tree of the graph (slightly modified so that each vertex of the original graph is in this tree; if the vertex $$$v$$$ is not an articulation point, it'll be a leaf connected to the corresponding biconnected component). Find the weighted centroid of such tree (the vertex after whose removal no subtree will contain more than $$$n / 2$$$ original vertices of the graph).
If this centroid is a biconnected component $$$X$$$ and one of the subtrees of the block-cut tree contains $$$\ge a$$$ original vertices, take that subtree to set $$$A$$$ and its complement to set $$$B$$$. Obviously, $$$|A| \ge a$$$, and $$$B$$$ is connected and $$$|B| \ge \frac{n}{2} \ge b$$$.
If this centroid is a biconnected component $$$X$$$ and all the subtrees contain $$$< a$$$ original vertices, create a weighted graph contracted to $$$X$$$ where each vertex $$$v \in X$$$ has its weight equal to the size of the component containing $$$v$$$ after removing all the edges in $$$X$$$. Each weight is $$$< a$$$, and $$$2a + b \ge n$$$, so we can apply the algorithm from Lemma 2 on $$$X$$$ to find two connected sets of vertices $$$A$$$, $$$B$$$ with total weights $$$\ge a$$$, $$$\ge b$$$. We can then expand the graph back, taking whole connected components to each set.
If this centroid is an articulation point and all the components created after its removal have size $$$<a$$$, the construction is impossible.
If this centroid is an articulation point and one of the components has size $$$\ge a$$$, take it to set $$$A$$$ and its complement to set $$$B$$$. Now, both $$$A$$$ and $$$B$$$ are connected and $$$|A| \ge a$$$, $$$|B| \ge \frac{n}{2} \ge b$$$.
Both of these cases are easy to check in linear time. Therefore, the task itself is solvable in linear time.
Well, I come up with the same idea about biconnected components, but it was looking very complicated, so I gave up and started merging shitty solutions to get 64 (°ー°〃)
For split, it seems to have numerous heuristics that is almost impossible to break.. I believe 64 points worked by trying all DFS spanning trees in each root.
I thought the same, but somehow organizers made tests really strong, kudos for that. I thought it would be impossible to break heuristics and this task will have like fifty solutions for 100pts, but only five of them would be legit solutions. It's great to see I was mistaken in that prediction.
No, it doesn't work. My solution is much harder (・へ・)
I tried every root and only got 40.
Sorry, can you please post your sketch of proof? I've been thinking about it for a while and it seems to me that there may be a counterexample. Consider a = b = c = n/3. Let's construct the graph like this: there is a clique of size 2*a-2. The other a+2 vertices we add as single edges attaching to distinct nodes in the clique. In this case we have a solution (consider one added vertex and a-1 vertices from the clique, times two), but if I understood your solution correctly, neither of your statements hold. The biggest biconnected component is of size less than a+b, and after we remove any articulation point we get components of sizes N-2 and 1.
Sorry, I don't post comments often so I don't know how to use math mode.
Oh shoot, you're right! I think I know how to fix this, but it's even more complicated and starts looking like "the model solution, only with extra steps". I'll try to edit my post in a moment. Thanks!
Edit: done, hopefully. I had a false statement in my proof that went like: "if after removing any articulation point $$$v$$$, there exists a connected component of size $$$\ge \frac{2n}{3}$$$, then there exists a biconnected component of size $$$\ge \frac{2n}{3}$$$". It's false, obviously. Silly me...
I want to share my idea for rect and split. (I haven't tried to implement yet, so please correct me if I'm wrong).
Rect:
First considering the condition:
(*) forall i, j: min(H[x1 − 1][j], H[x2 + 1][j]) > H[i][j].
In order for (*) to be true, we see that (x1 − 1, j) must be the first position such that H[x1 − 1][j] >= H[x2 + 1][j] if we move (x2 + 1, j) up or (x2 + 1, j) must be the first position such that H[x2 + 1][j] > H[x1 − 1][j] if we move (x1 − 1, j) down. From that observation, we can conclude that the number of states (x1, x2, j) satisfying the (*) condition is about O(2 * N * M).
So we can prepare all (x1, x2, j) states as well as (y1, y2, i) states.
After that, we can calculate the number of (x1, x2, y1, y2) states satisfying the problem condition with sweep line and a segment tree in O(N * M * log2(N * M)).
Split:
WLOG, assume that a <= b <= c. It's obvious that we always want to pick connected components with size a and b. Considering a spanning tree T from our initial graph G. We find the centroid node in T, called x. After removing x from T, we have m connected components V[1], V[2], ..., V[m]. We repeatedly perform the following operations:
If exists i (1 <= i <= |V|) such that |V[i]| <= a, we pick V[i] then stop.
Try to find an edge (u, v) such that u in V[i], v in V[j] and i != j. If found satisfied (u, v) go to the 3rd operation, else we stop.
We merge two components V[i] and V[j] and then go to the 1st operation.
Suppose that we cannot pick any components with size >= a (stopped at the 2nd operation), which means that we must use x (the centroid node) to create a component with size = a. However, if we use x, in the remaining components, we cannot find any components with size >= b >= a.
In other case, if we found a component V[i] with size >= a, we can use V[i] to create a components with size = a. Now, all we have to do is to prove |G / V[i]| >= b because we know that G / V[i] is a connected component.
Considering two cases:
V[i] is not created by merging two components V[x], V[y].
V[i] is created by merging two components V[x], V[y].
With case 1, we know that V[i] <= a -> |G / V[i]| = n − a >= n − a − c = b.
With case 2, we know that |V[i]| = |V[x]| + |V[y]| -> |V[i]| < 2 * a -> |G / V[i]| > n − 2 * a >= n − a − c = b.
I don't see how preparing (x1, x2, j) states easily helps you to solve the whole problem. Can you explain a bit more?
Well, after preparing all (x1, x2, j) and (y1, y2, i) states, you can merge two adjacent states together, for example (x1, x2, j) with (x1, x2, j + 1) or (x1, x2, j − 1).
So we can deduce to the new problem:
Given P rectangles of type 1: [(a1, b1), (c1, d1)] and Q rectangles of type 2: [(a2, b2), (c2, d2)]. Count number of pair rectangles x of type 1 and y of type 2 such that a1(x) <= a2(y) <= c2(y) <= c1(x) and b2(y) <= b1(x) <= d1(x) <= d2(y).
You can fix the segment [b1(x), d1(x)] and sweep line those segments [b2(y), d2(y)]. So all you need to do is to calculate the number of rectangles y such that a1(x) <= a2(y) <= c2(y) <= c1(x).
It seem that this kind of problem can only be solved in O(P * log2(N) * log2(M)). However, you can see that for every pair rectangles y1, y2 of type 2 that have overlapped area, there are only two cases:
a2(y1) <= a2(y2) <= c2(y2) <= c2(y1).
a2(y2) <= a2(y1) <= c2(y1) <= c2(y2).
With that observation, you can reduce the complexity to O(P * log2(Q)).
I got to all your points above, but I fail to see how that last observation reduces the complexity to $$$O(P\log Q)$$$. Can you elaborate?
You can sort all pair [a2(y), c2(y)]. For a query, you want to calculate the number of pair [a2(y), c2(y)] such that a1(x) <= a2(y) <= c2(y) <= c1(x).
To answer a query, first, you can calculate the number of pair [a2(y), c2(y)] such that a1(x) <= a2(y) <= c1(x). So all you need to do is to calculate he number of pair [a2(y), c2(y)] such that a1(x) <= a2(y) <= c1(x) < c2(y) (*) to subtract the result with this.
You see that all the rectangles of type 2 satisfying the (*) condition have overlapped area, so there are only two cases as I mentioned in the comment above. Or if we call S as the subset of rectangles of type 2 satisfying the (*) condition, it is true that:
a2(S[i]) <= a2(S[i + 1]) (0 <= i < |S| − 1).
c2(S[i]) >= c2(S[i + 1]) (0 <= i < |S| − 1).
You can find S[0] position and S[|S| − 1] position on the segment tree by storing something like (does this segment contain an element equal to 1, if it does what is the maximum c2 value of an element equal to 1).
UPD: I just realized that my above solution is wrong. So I'm very glad to hear another solution if possible.
For the purpose of medal allocation, after day 1 the official number of contestants is 327. (This number cannot go down after day 2, and most likely it should not change.)
Isn't it 331?
No, 327 is the number we were told at the meeting after day 1. AFAIK, four of the contestants who were shown in the online results are contestants who were registered for the IOI but did not take part in day 1. The most likely reason is that they are not here and they won't take part in day 2 either, but I don't know for sure whether this is the case. (And in the past there were some cases when some contestants only took part in day 2 for various reasons.)
There was an accepted appeal that still is being worked on that may or may not result in the score change, so at this point results of Day 1 are not final.
Can you tell what appeal is about?
According to ISC, some contestant or contestants were not able to submit during the final moments of the contest due to CMS slowness. If any of that submission would've gotten a bigger score, it may be submitted manually and the score would be updated. My understanding is that there are backups of workstations at the time of contest end, so any changes made during the analysis shouldn't be a factor.
Im not 100% sure if i managed to change it in time, but i might have an ac code for shoes on the machine at the time when the contest ended. Is there some chance that someone can check that? I will provide details if it's possible.
Edit: i guess that i have to do that with my team leaders and it too late for that now, plus im not sure if the appeal is valis and its "only" 15 points so it doesn't matter that much.
Yes, officially it's the case that your team leader has to submit an appeal. Before dinner we were told to submit these appeals if we have them and didn't submit them before, and there was no strict deadline on this. Get in touch with your leader, you have nothing to lose by doing so. Ideally, send them the exact name and location of the file you want rejudged.
(Edit: I would recommend that your leader should send the details to the ISC by email ASAP and to formally file an appeal on paper later, if required.)
There just was an e-mail distributed amongst GA that if students were affected by the issue at the end of the contest, and haven't yet submitted an appeal, that the deadline is tomorrow noon (in ~13h from now). So definitely contact your leaders! You'll need exact path and filename on your machine to be evaluated.
I did that, thanks! Now i can just hope :)
Is it about the solution for p3?
...is held in a beautiful city of Baku, Azerbaijan this year.
Sorry for the offtopic, but maybe you should have written " a beautiful city of Azerbaijan, Baku " ?)
it is correct both ways, in the post's way it is denoting (city, country) pair as one unit
Benq is so strong.
I don't know who are you talking about, but 300iq will smash him tomorrow.
grabs popcorn
*at the icpc finals
Well, he got bigger score indeed. By 0.13 xd
٩(๑òωó๑)۶
Anybody knows how to solve walk problem?
It seems sad that line problem can be solved in a fully provable way (what problem highly suggested, right?), but nobody solved it and it boiled down to basically pushing through some garbage heuristics. However I don't know how to solve it as well, so I am not to blame contestants, but just stating fact that it's sad :P.
Well I don't think that problem highly suggested it. I didn't thought that it is possible to solve in provable way lol. Maybe n+3 is just a parameter they used for test generation
There's a relatively easy $$$n+3$$$ solution.
Yeah I know now, but during the contest it was not clear for me that it is solvable for any test case in n+3
Ok, but in general: why would a problemsetter set a problem that cannot be fully solved (I mean the one that doesn't have 100pts solution)?
What about nowruz? I thought that it is the problem of the same type.
We don't talk about this problem.
I mean I thought that line is the same type as nowruz.
BOI 2019 Flash 100 points in this task is the theoretical maximum if you have infinite time. Nobody knows the 90+ solution as far as I know.
Huh, because 90% of output-only are not meant to be solved in a provable way? Fact that solution for given instances with <=n+3 exists is significantly different than fact that any instance you can imagine has solution with <=n+3 segments. A priori it is possible that tests were generated by creating some broken line with <=n+3 segments and marking some points on them what makes it very easy to create test like that which would then be hard to solve (similar to as it is easy to generate a graph with hamilton cycle, but it is hard to find it afterwards).
So, my conclusion is that contestants could definitely suspect that some general provable algorithm exists, but can't be sure about it.
How to solve in n+3 segments?
We decompose the point set into three sets:
If this is possible, then we can connect from (0, 0) to increasing set, then decreasing, and windows set with only 3 extra segments. (There are technical details, but you can figure it out)
This is possible, and the proof is constructive. We use induction on size $$$n$$$. If $$$n \le 1$$$, trivial. Otherwise, we consider the "bounding box" which is the minimal axis-parallel box that encloses the set. There is at least 2, and at most 4 distinct point that lies in the edge of bounding box. Now we divide cases:
Since the bounding boxes are always shrinking toward the center, it's clear that the increasing / decreasing sequences are valid, and it's not hard to connect them optimally.
Now we consider how to connect the vertices in windows set. Again we can see the windows are shrinking toward the center. It seems they can be simply connected by spiral strategy, but in fact, it's NOT. Instead, you start from the smallest windows. Cover all four vertices by some cycle and proceed to the next windows. In the next windows, you can either turn in CW direction or CCW direction. Set the direction appropriately to cover the point that lies in the windows segment you encountered. This strategy never creates wasteful segments.
Implementation is in my github.
AFAIK it's solvable for every instance in $$$N+3$$$. I'm aware of the basic idea, but that's all :(
Giving a normal problem as an output only has several pros and cons. For the good thing, the contestants were given visualizers, so they can easily spot what's going on (very helpful for a tricky problem like this), plus the scoring system can help break ties. For the bad thing, it gives room for ad-hoc test analysis and garbage heuristic which isn't science at all. And due to some bad past practices on OO tasks, contestants might consider the search for $$$N+3$$$ solution as a "risky strategy".
In general, I think the contestants got what they deserve, but some might consider the "naive spiral strategy" as garbage and should not get more than 10 points. I don't have a very strong opinion about that...
How many points did spiral give? Indeed seemed garbage to me (however on random test I guess it should be ok), but I didn't try it
About 50 points.
People over 90 points did something provable, I think.
Lol I have 90+eps and I just used some greedy.
My solution(try going in the same direction as previous one by, for example, if the last line was going up, going to a point above the last point; try to keep yourself in the middle by taking the point with the median x coordinate out of all the candidates if you're going up or down and taking the point with the median y coordinate out of all candidates if you're going left or right; it's n^2 log n but TL is 5 hours) gets between 2 and 6 points on all tests which are structured like diagonal lines(i think tests 2 and 7 were crosses, test 5 looked like this: and test 4 was a diagonal line) and more than 9 points on all other tests. The union of my solution and my teammate's solution(decompose the input into a small amount of monotone sequences and handle each of them separately) seems to get 88 points.
and test 4 was a diagonal line) and more than 9 points on all other tests. The union of my solution and my teammate's solution(decompose the input into a small amount of monotone sequences and handle each of them separately) seems to get 88 points.
Did anyone solve vision with prefix xor over columns/rows and addition of H + W bits?
I did that in the contest.
I think the easiest solution is to do prefix xor on diagonals and check if $$$dist >= K$$$ and check $$$>=K+1$$$
Can you write how to do that exactly?
I think $$$|r_1-r_2|+|c_1-c_2| = max(|r_1+c_1-r_2-c_2|,|r_1-c_1-r_2+c_2|)$$$. If you do prefix xor for diagonals $$$(i+j)$$$ and $$$(i-j)$$$ when you will have some consecutive number of ones (let's say $$$a$$$ and $$$b$$$). We need to check that $$$max(a, b) = K$$$. That means $$$max(a,b)>=K$$$ is true and $$$>=K+1$$$ is false. To check if $$$a>=C$$$ try anding $$$(i)'th$$$ and $$$(i+C)'th$$$ element.
Can anyone verify my solution to walk?
Naive solution (24 points?) makes vertices for all intersection. We do some optimizations by only building only the following intersections:
Then we run Dijkstra on that graph.
Nah, that won't work.
You will not detect the intersection marked with dot.
(Edited after ~300iq pointed out my previous counterexample was wrong).
I think it will detect it, cuz this intersection is adjacent to the right vertex of the upper segment.
Whoops, sorry, thanks. However I still think it doesn't work and I will update the picture in a second.
You don't need to detect intersection?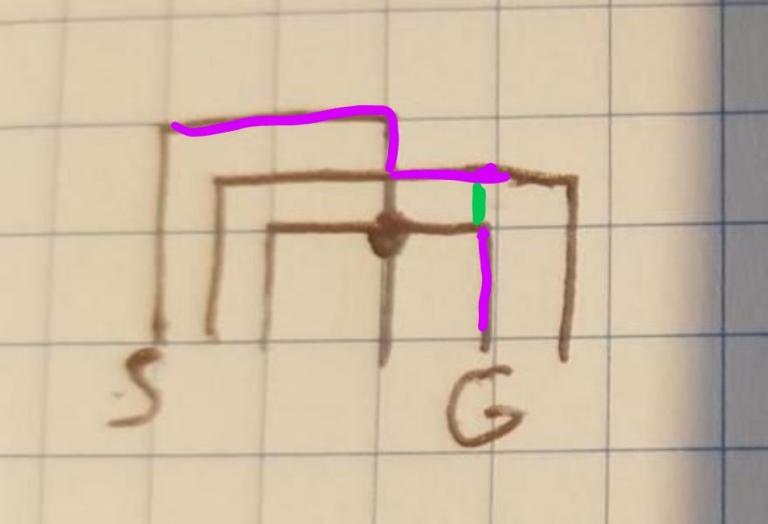
Green is that "escape" edge.
Where does the green line come from? You can't just add it in.
When the horizontal segment ends, we make an "escape route vertices", where we make vertices for two horizontal segments, vertically adjacent to that endpoint.
You are making escape edges too.
Escape edges have to be along an existing vertical pole; otherwise, we allow some invalid solutions.
I think that we need to add some escape edges without existing pole, if they are correct. Without it this solutions is completely incorrect.
But I am not sure if what I am saying makes sense.
It's true you sometimes can, but it doesn't work in general. I think if you can show that you're only moving left->right, then you're allowed to, but it actually could be wrong for this case.
For instance, consider
Adding an escape edge upwards from S to the top bar would illegally shorten the path.
This doesn't work (as described by Swistakk), but here's a modification which I'm pretty sure does:
For each horizontal segment, insert vertices:
Also, insert vertices at the intersections on poles directly above and below all the ones we listed. This gives $$$\le 18 M$$$ vertices, and then we run Dijkstra.
I solved it in contest using the exact same way. I didn't prove the correctness, though.
tmwilliamlin168's insane comeback was probably the best thing to watch in day2, change my mind.
Too bad he had a awful day1 :(
Nope, you got it wrong. tmwilliamlin168 performed horribly in day 1 intentionally just to make this ultra-awesome comeback in day 2. No one can ever match the geniosity. Ever. tmwilliamlin168 orz
Can someone explain what orz means, I've seen it a hundred times in codeforces.
orz is a person bowing down on the ground. If you look carefully and squint your eyes you can see it. The "z" is the legs, the "r" is the body, and the "o" is the head
One thing to note is that whenever "orz" is used on me, it is always sarcastic.
One thing to note is that when ultra-awesome genius pr0s respond to compliments, it is always sarcastically.
You are such a great person because of your humility!
IOI 2019 preliminary results are available on IOI Stats.
Top 5 are all Chinese, such strong country.
300iq is not chinese.
read this
It was a joke as redocyz replied, but I guess my since of humour is bad.
Is country rank based off of sum? Or lexicographical order of medals? I guess the latter is a tad bit more favorable to Korea ;) Anyway, congratulations to your team on a great performance!
Thank you, and congratulations for team USA! I think the former is better, but we (our government?) always considered country rank based on medals. Even in 2015, where we were the absolute 1st place in score order, we used medal based rank :)
Why did sunset perform so poorly, taking only 49th place, who knows?
To leaders: how many appeals were there and how close is this preliminary result to a possible outcome?
I have not heard about any changes to the results during the meetings or some private conversations with other leaders. In other words, I have no reason to believe that any major changes will be made to the scoreboard.
Of course, I could be wrong...
(I am the USA deputy leader.) There are between 5 and 10 appeals, maybe one or two still under review. In general, the vast majority of appeals are rejected.
My understanding is that several instances of accepted appeal for first day are still in progress.
I stumbled upon a post by Olimpiada Informatyczna. As my Polish is very basic I gladly used the Facebook translator. But what does the following sentence mean?
Better check the original!
Not cool, Facebook!
It's not FB's fault, it's the algorithm's fault! (Classic excuse when something goes wrong.)
Or it must be those Russian hackers FB and similar media worried about so much.
'I spent the evening mostly with the Georgians, Bulgarians, Estonians, Russians, Ukrainians and Belarusians practicing my Russian.'
The blog made by Polish leaders is amazing! Though they haven't written that in English :(
If we will have some international audience, we might consider translating our posts.
<3
The GA have voted to approve IOI 2019 results and medal allocation.
There have been several changes of scores from preliminary results as results of appeals but none have resulted in changes in medal allocations.
Can you add cf accounts in ioi stats?
Yes, will do in a couple of days.
Done. More information.
Tests when?
Does anyone have solutions and\or test data for the problems?
They will be published soon (TM) on the official website here: https://ioi2019.az/en-content-27.html
How to solve problem walk? At least for 57 points
The first 2 subtasks are trivial (just run dijkstra).
For subtask 3, you will only go right since you should never visit the same building twice. We can write a DP solution, where dp[i][j] = min cost to get to building i at height j. We can use a set to do this efficiently.
Subtask 4 seems harder than subtask 3 since the heights are not equal, but...
That's because in subtask 4 (go from first building to last) you also only need to move to the right.
Not just that, you can also assume that all heights are equal in subtask 4.
How do you make that dp with set in less memory and time? Because there can be many intersections
Use set of $$$(j, dp[i][j] - x_i)$$$ don't store value if $$$dp[i][j]=dp[i][k] + |j - k|$$$ for some $$$k\neq j$$$.
What if you have to store many values still?
Use sweeping line, many values do not change.
You can submit all problems except Rectangles here: https://oj.uz/problems/source/420
It seems someone forgot to make
rect.zippublic on the folder here..Which sheepfuckers are downvoting this? Finally a place to submit.
Now all problems (including the practice contest) are ready! https://oj.uz/problems/source/420
nice
Can somebody explain the solution for task vision, I got up to 66 points, but I couldn't think of anything better, also I couldn't find any editorial on the internet.
Look at my comment.
Official live streams of both contest day contains analysis of all the problems: Day 1, Day 2