Доброго времени суток! Началось все с того, что после прочтения статьи про встречное дерево Фенвика, я начал искать в интернете его реализацию, но (спойлер) так и не нашел. Безусловно, тема не нова, но, к сожалению, статью, описывающую эту структуру данных с приведенными примерами реализации, я так и не нашел. Перед прочтением данного поста советую ознакомиться с указанной статьей, т.к. на нее будут опираться все дальнейшие рассуждения.

Встречное дерево Фенвика

Для начала, вспомним определение: Встречное дерево Фенвика (англ. counter tree Fenwick) — дерево Фенвика, в котором над каждым столбцом идет столбец такой же высоты, вычисляемый по формуле $$$f_{rev}[i]=\sum\limits_{j=i+1}^{i+2^{h(i)}}a[j]$$$. Сразу сделаю уточнение, что под прямым деревом Фенвика подразумевается массив, посчитанный формуле: $$$f_{for}[i]=\sum\limits_{j=i-2^{h(i)}+1}^i a[j]$$$. Для пущей понятности, прикреплю картинку.

Зная только то, что встречное дерево Фенвика симметрично прямому, мы можем написать код для построения встречного и прямого деревьев Фенвика, где F — функция, значение которой мы хотим считать на отрезках:

void bit_build(int n, int src[]) {
	int m = 1; while(m < n) m *= 2; m -= 2;
	for(int i = 0; i < n; ++i) {
		a[i] = src[i]; // прямое дерево Фенвика
		b[i] = i+1 < n ? src[i+1] : NEUTRAL; // встречное дерево Фенвика
	}
	for(int i = 0, j; i < n; ++i) {
		const int j = i|i+1;
		if(j < n) a[j] = F(a[i], a[j]);
	}
	for(int i = m-n+2; i < m; ++i) {
		const int j = i|i+1;
		const int u = m-i, v = m-j;
		if(j < m) b[v] = F(b[v], b[u]);
	}
}

При $$$n=2^k$$$ видно, что отрезки, покрываемые прямым и обратным деревом Фенвика идентичны дереву отрезков длины n. Из этого видно, что любой отрезок делится на два других отрезка так, что один из них полностью покрывается встречным деревом Фенвика, а другой — прямым.

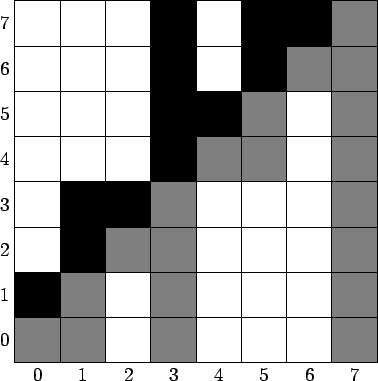
Остается только сопоставить получившееся дерево Фенвика и ДО. Представлю иллюстрацию для случая n=8.

Отсюда становятся очевидными три важных факта:

1. Каждая вершина ДО (кроме листьев) составленная из элементов дерева Фенвика имеет две дочерние вершины, имеющие одинаковые индексы, но одно из них лежит в прямом дереве Фенвике, а другое во встречном.

2. В двоичной системы счисления номера листья оканчиваются на "0", вершины лежащие на втором снизу уровне обладают суффиксом "01", на третьем — "011", четвертом — "0111" и т.д.

3. Номера вершин ДО, лежащих на одном уровне, строго возрастают в порядке слева-направо.

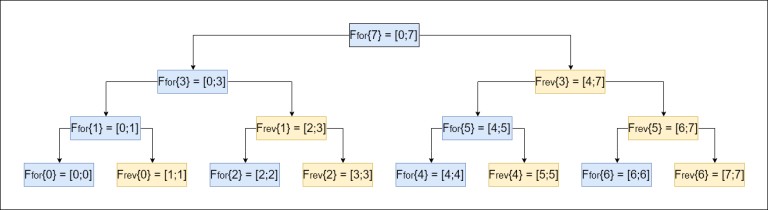
Рассматривая номера вершин на пути от листа $$$v$$$ легко проверить, что все вершины при их записи в двоичной системе счисления будут иметь префикс такой же, как у $$$v$$$, но суффикс будет другим, в зависимости от того, на каком уровне лежит вершина. Массив же, которому принадлежит вершина будем определять непосредственно смотря на значение очередного бита в номере листа. Пример пути от листа до верхней вершины дерева отрезков для позиции номер 20 в массиве.

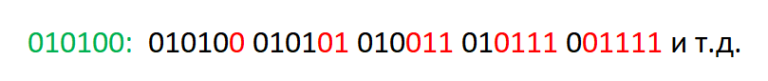
Дальше, я надеюсь, идея обновления значения элемента в массиве становится понятной — просто обновляем значение листа, отвечающего за значение нужного элемента массива и идем вверх, пересчитывая значения всех рассматриваемых вершин. Поиск значения функции F на отрезке я описывать не буду, потому что (а) мне лень, и (б) алгоритм очень схож с поиском ответа на запрос в обычном дереве Фенвика, только в нашем случае мы дополнительно используем встречное дерево Фенвика.

// Обновление произвольного элемента в массиве
void bit_update(int id, int val) {
	if(id&1) id=id^1, b[id] = r; // в зависимости от четности обновляем значение в нужном массиве
	else              a[id] = r;
	for(int j = ~1, t=2, z=1, p=id; ; z=z|t, t=t<<1) {
		j = j^t; const int v = id&j|z; if(v >= n) break;
		// При рассмотрении следующей вершины будем учитывать, что обе дочерние вершины
		// имеют одинаковый индекс, т.е. находить их явно, нам не надо.
		if(id&t) b[v] = F(a[p], b[p]);
		else     a[v] = F(a[p], b[p]);
		p = v;
	}
}

// Ответ на запрос
int bit_ask(int l, int r) {
	int res = NEUTRAL;
	for(; (r&r+1) >= l && r >= l; r=(r&r+1)-1)
		res = F(a[r], res);
	for(; (l|l-1) <= r && l && l < n; l=(l|l-1)+1) 
		res = F(b[l-1], res);
	return res;
}

Код RMQ с использованием данной структуры:

#include <stdio.h>

const int N = 1e5+7, MINF = -1e9;

int n, dx, m, a[N], b[N];

constexpr static int calc_dx(int n) {
	int dx = 1, tmp = 0; while((tmp = dx << 1) < n) dx = tmp;
	return dx;
}

int main() {
	scanf("%d", &n); dx = calc_dx(n);
	for(m = 1; m < n; m *= 2); m -= 2;
	for(int i = 0; i < n; ++i) {
		scanf("%d", &a[i]); if(i) b[i-1] = a[i];
	} b[n-1] = MINF;
	
	for(int i = 0, j; i < n; ++i) 
		if((j=i|i+1) < n && a[j] < a[i]) a[j] = a[i];
	for(int i = m-n+2; i < m; ++i) {
		const int j = i|i+1;
		const int u = m-i, v = m-j;
		if(j < m && b[v] < b[u]) b[v] = b[u];
	}

	for(scanf("%d", &m); m--; ) {
		char s[9]; int l, r;
		scanf("%s%d%d", s, &l, &r);

		if(s[0] == 'u') {
			int id = l-1;
			if(id&1) id=id^1, b[id] = r;
			else              a[id] = r;
			for(int j = ~1, t=2, z=1, p=id; ; z=z|t, t=t<<1) {
				j = j^t; const int v = id&j|z; if(v >= n) break;
				if(id&t) b[v] = a[p] > b[p] ? a[p] : b[p];
				else     a[v] = a[p] > b[p] ? a[p] : b[p];
				p = v;
			}
		}
		else {
			int res = MINF; --l; --r;
			for(; (r&r+1) >= l && r >= l; r=(r&r+1)-1)
				if(res < a[r]) res = a[r];
			for(; (l|l-1) <= r && l && l < n; l=(l|l-1)+1) 
				if(res < b[l-1]) res = b[l-1];
			printf("%d ", res);
		}
	}
}

P.S.: Сегодня протестировал свою программу на рандомных и не совсем рандомных тестах при различных ограничениях. По скорости сравнивал с этой реализацией ДО. Оказалось, что ДО все же быстрее, при большом количестве запросов разница достигает 100мс. Выводы можно делать разные, например oversolver предположил, что реализация встречного дерева Фенвика, где индексация будет начинаться не с нуля, а с единицы, может оказаться быстрее. Ну что ж, в ближайшее время постараюсь проверить.

Таблица с результатами: