I recently took part in Codeforces Round 976 (Div. 2) and Divide By Zero 9.0, and I performed ... poorly (only A after 6 bad submissions). Thinking about this traumatizing experience, I first tried to find excuses. I entered 15 minutes late, I was sick and unprepared. But I realized that there were more to learn from it, and I wanted to try and produce a custom editorial of the first 4 problems in the contest to better understand and share what I did wrong (and also perhaps right thing :)).

Welcome to my humble editorial

2020A - Find Minimum Operations

The first step was to understand the structure of the optimal solution. For given $$$n$$$ and $$$k$$$, the optimal number of operations is obtained by removing the largest possible portions of $$$n$$$ of the form $$$k^x$$$ at each step, i.e. finding the largest $$$x$$$ such that $$$k^x \leq n$$$.

The algorithm is as follows :

while n > 0
    x = findLargestX(n,k)
    while n-k^x > 0
        n -= k^x

I was quickly able to see that the answer is the sum of the digits of $$$n$$$ in base $$$k$$$. This helps to understand why the algorithm works, and why we should find the largest $$$x$$$ value at each step.

It is more clear with an example. In the fourth test case, $$$n=100$$$ and $$$k=3$$$. $$$(100)_{10} = 1*3^4 + 2*3^2 + 1*3^0 = (10201)_3$$$. The answer for the test case is then $$$1+2+1=4$$$.

I know that $$$x = \lfloor log_k(n) \rfloor$$$.

I wrote it as $$$(\textbf{ull})(log_2(n) / log_2(k))$$$ and got wrong answer on pretest 2. I wasn't sure to understand how to handle edge cases in double division and casting. A better idea was to look directly for $$$k^x$$$.

My first try was to write a while-loop in $$$\mathcal{O}(x)$$$ to find the largest $$$k^x \leq n$$$. This got time limit. It is only after trying B and coming back that I realized it could be done in $$$\mathcal{O}(log(x))$$$ with a syntax similar to fast exponentiation.

int main() {
    int t;
    cin >> t;
 
    ull n, k;
    while(t--) {
        cin >> n >> k;
        ull ans = 0;
        if(k > n || k == 1) {
            ans = n;
        } else {
            while(n > 0) {
                if(k > n) {
                    ans += n;
                    break;
                }
                ull l = k;
                while(l*l <= n) l *= l;
                while(l*k <= n) l *= k; 
                n -= l;
                ans++;
            }
        }
 
        cout << ans << endl;
    }
 
    return 0;
}

What I learnt

• Don't rush even into simple problems.
• It is great to identify known results, but using "black-box" numerical approaches might not be the best idea when designing an exact algorithm
• When writing a loop in $$$\mathcal{O}(n)$$$, ALWAYS look for a way to simplify it in $$$\mathcal{O}(log(n))$$$, $$$\mathcal{O}(1)$$$ for example.

2020B - Brightness Begins

It is necessary here to think about the structure of the answer. First of all, considering $$$n+1$$$ bulbs instead of $$$n$$$ doesn't change the state of the first $$$n$$$ bulbs. A bulb at position $$$k$$$ is flipped once for each divisor of $$$k$$$. All on bulbs will be located at positions with an even number of divisors.

I thought of the prime factor decomposition of a number, from which it is easy to compute the number of divisors.

However, the answer had to be greater than $$$k \leq 10^{18}$$$, so complete decomposition was not an option.
In fact, even $$$\mathcal{O}(n)$$$ was probably too long.

I was missing the fact that in terms of product, there are more even number than odd number.

If the power of any prime divisor in the decomposition of $$$n$$$ was odd, then the number of divisors $$$n$$$ would be even. In consequence, the only number with an odd number of divisors would be those with all even powers in the PFD, i.e. perfect squares !
Drawing the bulbs with $$$n=10$$$ really gives this up :

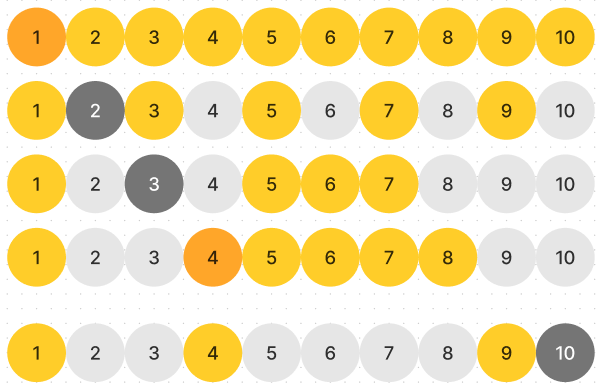
For a given $$$n$$$, the number of perfect squares below or equal to it is $$$\lfloor \sqrt{n} \rfloor$$$, and the number of on bulbs $$$n-\lfloor \sqrt{n} \rfloor$$$. Using binary search, it is possible to look for $$$n$$$ the smallest number of light bulbs.

My code is as follows.

ull k;
while(t--) {
    cin >> k;

    ull l=k, r=4*k;

    while(r-l>1) {

        ull m = (r+l) >> 1;
        ull perfectSquares = sqrtl(m);

        if(m-perfectSquares >= k) r=m;
        else l=m;
    }
    cout << r << endl;
}
cout << (ull)sqrt(854258780613619263) << endl;
return 0;

During the contest I fumbled a lot and wasn't able to find the right condition to update $$$l$$$ or $$$r$$$, that's on me. But as I came back after the contest, I still had WA. For $$$k=854258779689358055$$$, my answer was $$$854258780613619263$$$ when it should have been $$$854258780613619262$$$.

I knew it was once again related to how I used a blackbox double sqrt function for an integer program. After investigating, (\textbf{unsigned long long})$$$sqrt(854258780613619263) = 924261208$$$, which is incorrect. To avoid numerical error, I should've used (\textbf{unsigned long long})$$$sqrt($$$(\textbf{long double}) $$$854258780613619263$$$) (or $$$sqrtl(854258780613619263)$$$).

What I learnt

• Once again, I lost time thinking about complex DFP solution and not see the simpler pattern. Don't rush into complex thinking immediately
• Sometimes, using graphical hits can help to identify patterns
• I guess I miss experience with numerical programmation, and I'll try to remember this edge case in the future

2020C - Bitwise Balancing

I read the problem during the contest and I saw that it would be mostly writing a truth table, and I didn't had time to really start it.

My solution is basically the same as in the official tutorial. One can see that each bit can be processed independently (by making sure (a|b) — (a&c) cannot be -1). By building a truth table, I was able to write a solution quickly.

What I learnt

Not much, I didn't find the problem very educational

2020D - Connect the Dots

I tackled the problem a few days after the contest. First, it looks like a classic Disjoint Set Union problem. Each operation can be computed $$$k$$$ query by considering arcs ($$$a$$$, $$$a+d$$$), ..., ($$$a+(k-1)*d, a+k*d)$$$. I was able to implement it quickly using my DSU template, but got TL without much surprise.

forn(i,1,m) {
    cin >> a >> d >> k;
    forn(j,0,k-1) dsu.merge(a+j*d, a+(j+1)*d);
}

In a static graph, it seems to me that there is no reason to use DSU over DFS (except I didn't have a DFS template at the time). But this isn't the reason for my TL, counting components using DSU with path compression has a nearly linear complexity.

For each query $$$1\leq q \leq m$$$ I'm creating $$$k_q$$$ edges, resulting in $$$\sum_{q=1}^{q=m}k_q$$$ edges. If ranges are disjoint, this can't be reduced. But since $$$k$$$ can be large w.r.t. $$$n$$$, ranges may have many overlap. For example, let's take $$$(4,2,6)$$$ and $$$(2,2,5)$$$. They overlap on 4 edges ! This is because they share the same gap $$$d$$$. But they could in phase opposition. These two ranges can overlap because they both started at a position with the same rest in the division by $$$d$$$ ($$$4\%2 == 2\%2 == 0)$$$.

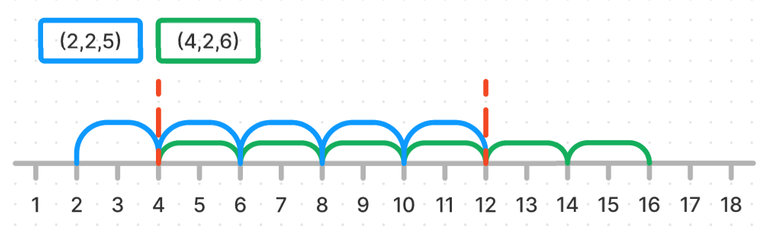
I thought I could take advantage of $$$d \leq 10$$$. For a position $$$a$$$, and each value of $$$d$$$ I need to know if I must create an edge $$$(a,a+d)$$$, i.e. if there exists at least one range with step $$$d$$$ containing $$$a$$$. For such a query to exists : - it begins before $$$a$$$ and ends after $$$a$$$ - it has step $$$d$$$ - the rest in the division by $$$d$$$ of any of its values is $$$a\%d$$$

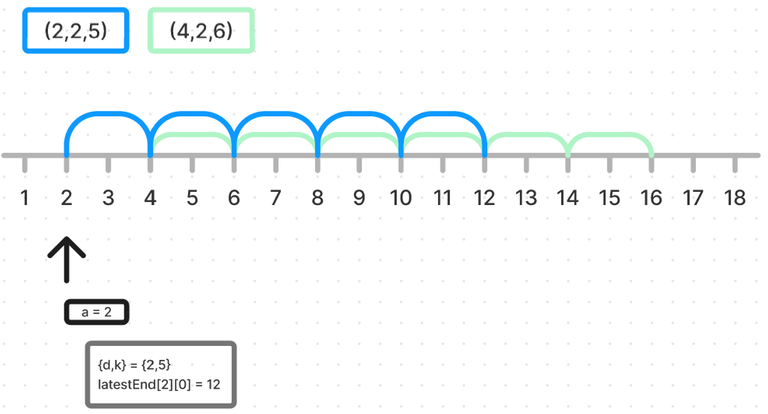
I use a table $$$latestEnd$$$ of size $$$11*10$$$. The first index is associated with the value of $$$d$$$ and the second index with the value of $$$a\%d$$$. For each $$$a$$$, I consider the end of the range of each starting query in $$$queries[a]$$$. If I meet new queries with same characteristics (possibly overlapping), I can what the new latest end is.
Then for each value $$$d$$$ in $$$[1,10]$$$, I test if a range of step $$$d$$$ and offset $$$a\%d$$$ ends after $$$a$$$. If so, I create an edge $$$(a,a+d)$$$.

In the above example, when reaching $$$(2,2,5)$$$, I need to register that I activated a range of step $$$d=2$$$ with offset $$$a\%d = 0$$$ ending in $$$a+d*k = 12$$$. For $$$a=4,6,8,10$$$ and $$$d=2$$$, I can check that a previously started range of step $$$d$$$ and offset $$$0$$$ ends after $$$a$$$, i.e. contains it, and create the edge $$$(a,a+d)$$$.

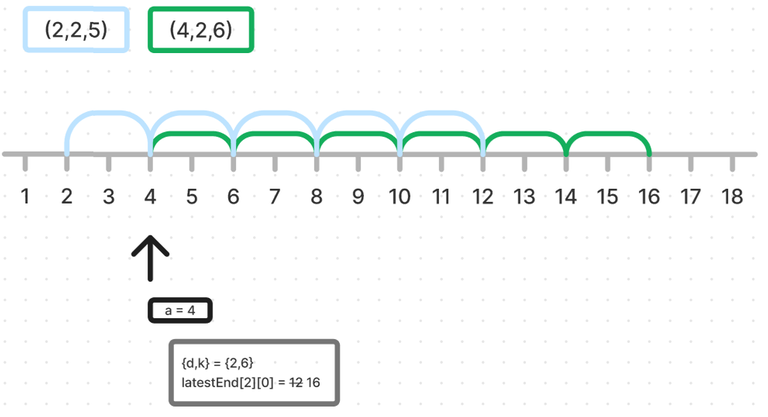
Later when reaching $$$(4, 2, 6)$$$, the range shares values $$$d=2$$$ and $$$a\%d = 0$$$, but ends later in $$$a+d*k = 16$$$, and I need to notify further values of $$$a$$$ up to $$$16-2 = 14$$$ s.t. $$$a\%2 = 0$$$ to create an edge $$$(a,a+d)$$$

#include <bits/stdc++.h>
#include <vector>


using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define forn(i,j,k) for(ll i=(j); i<=(k); i++)
#define rofn(i,j,k) for(ll i=(j); i>=(k); i--)
#define forv(b,a) for(auto &b : a)
#define dbg(n) cout << n << endl;


struct DSU {
        vector<ll> parent;
        vector<ll> size;

        void init(ll n) {
            parent.resize(n);
            size.resize(n);
            for(ll i=0; i<n; i++) {
                parent[i] = i;
                size[i] = 1;
            }
        }

        //With path compression optimisation
        ll find(ll a) {
            if(a == parent[a]) return a;
            return parent[a] = find(parent[a]);
        }

        //With size balance optimisation
        void merge(ll a, ll b) {
            a = find(a);
            b = find(b);
            if(a != b) {
                if(size[a] < size[b]) swap(a,b);
                parent[b] = a;
                size[a] += size[b];
            }
        }
};

int main() {
    ll t;
    cin >> t;

    ll n, m;
    ll a, d, k;
    while(t--) {
        cin >> n >> m;

        vector<vector<pair<ll, ll>>> queries(n+1);
        forn(i,1,m) {
            cin >> a >> d >> k;
            queries[a].push_back({d,k});
        }

        DSU dsu;
        dsu.init(n+1);

        // Stored by step d and by rest in the division by d
        vector<vector<ll>> latestEnd(11, vector<ll>(11, -1));
        forn(a,1,n) {
            for(pair<ll, ll> q : queries[a]) {
                d = q.first; k = q.second;
                latestEnd[d][a%d] = max(latestEnd[d][a%d], a+k*d);
            }
            forn(d,1,10) {
                if(latestEnd[d][a%d] > a) {
                    // Query is active
                    dsu.merge(a, a+d);
                }
            }
        }

        vector<bool> visited(n+1, false);
        ll ans = 0;
        forn(i,1,n) {
            ll rep = dsu.find(i);
            if(visited[rep]) continue;
            visited[rep] = true;
            ans++;
        }

        cout << ans << endl;
    }

    return 0;
}

What I learnt

This was a very interesting problem. I many differents answers in the comments of the official editorial, from which I should maybe learn :
- A first classical algorithm a good start to have a working solution
- In case of TL, it's important to identify the main sources of complexity
- One can take advantage of some parameters domain specified for the problem.
- When working with ranges, you most likely want to identify overlapping ranges to reduce duplicated data, i.e. using dp.

Conclusion

I'll stop here. Being able to solve 4 problems in a Div. 2 contest is a reasonable goal. I really appreciated doing this blog, and I hope it can benefit or amuse some fellow codeforcers. I'll eventually write another one after my next contest, even if my performance happens to be less disastrous.
Thank you P.V.Sekhar and nishkarsh for organizing this contest, and MikeMirzayanov for platforms Codeforces and Polygon.