Всем привет. Сегодня прошёл очередной гран-при открытого кубка по задачам ICL.
Расскажите, пожалуйста, решения задач H, J, K.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:55:15
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:55:15
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 09:39:47 (j3).
Десктопная версия, переключиться на мобильную.
При поддержке
В K в дорешке зашло такое: Заведём N hash-сетов. Запишем в i-ый сет хеши всех префиксов длины i слов первого множества. Дальше, для каждой позиции во втором множестве слов, делаем бин-поиск по длине, проверяя, встречался ли такой хеш.
Код: http://pastebin.com/F06xuUCD
Обидно, что в K это заходило.
У нас за линию: делаем как в алгоритме построения z-функции, только вместе с "окном" храним еще вершину бора, которая ему соответствует, и при переходе вправо на символ идем по бору (а при сдвиге левой границы окна вправо — по суффиксным ссылкам бора).
K — кидаем хеши всех префиксов исходных строк в хеш-таблицу, для ответа на запрос используем простой бинпоиск (по ответу) + поиск в хеш-таблице.
J — переберем позицию центра палиндрома, найдем с помощью, к примеру, бинпоиска с хешами, насколько его максимум можно расширить в одной строке (легко убедиться в том, что выгодно всегда расширять по максимуму), а после этого еще одним бинпоиском найдем, насколько можно расшириться, задействуя другую строку.
H — попробуем решить задачу для одной стороны многоугольника, давайте вместо того, чтобы доходить до стороны, потом идти по ней, сначала пройдем по вектору, параллельному стороне (здесь лучше просто нарисовать картинку). Теперь нам нужно дойти до стороны, а потом идти куда-то еще. Воспользуемся следующим трюком: отразим точку относительно этой стороны, теперь нам уже просто надо идти по прямой куда-то (т.к. расстояние при отражении останется тем же). При этом, в теории у нас мог бы возникнуть случай, когда наша точка оказалась не по ту сторону от следующего ребра, но тогда бы ответ проходил через вершину многоугольника, что по условию невозможно. Возможно, это звучит сложно, но если нарисовать картинку, то все станет понятно.
К слову, H совершенно нахаляву сдавалась локальными оптимизациями — берем произвольную ломаную в качестве начальной и начинаем по очереди каждое звено сдвигать так, чтобы со своими соседями оно образовало оптимальное положение. 500 раз по порядку все звенья шевелим и получаем AC минут за пятнадцать.
Можно легко объяснить, почему это полное решение и оно должно работать — если взглянуть на ответ — как на функцию от положений отрезков на каждой стороне многоугольника, то она будет выпукла по каждой переменной, а значит у нее только один глобальный минимум, даже когда мы ее ограничим условием, что отрезок должен лежать на стороне. Локальными оптимизациями мы сойдемся в какой-то локальный минимум, он же окажется глобальным. Вот так.
Не знаю, зачем так акцентировать внимание на времени написания вашего решения; геометрическое решение писалось 7 минут: нужно уметь отражать точку относительно стороны и сдвигать ее на вектор. Да еще и работает для нормальных ограничений:)
Возможно, но учитывая общее качество подготовки контеста (а именно облом с задачей F), я бы не был так уверен что это отработает на любом тесте.
Результаты финала ICL отдельно (возможно, с точностью до округления).
А как решать A и D?
D: зашел перебор с отсечениями. Перебираем числа в порядке возрастания, на каждом шаге выгодно добавлять либо последнее число еще раз, либо сумму всех чисел + 1. Запускаем такой перебор с ограничением суммы 100000 и попутно оффлайново обновляем ответы на запросы.
В D есть решение и без перебора (например, за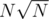
). Заведем динамику d[N] (собственно, то, что у нас спрашивается в задаче): минимальное количество чисел для суммы N. Тогда если m — это максимальное число в наборе и его взяли cnt раз, то остальные (меньшие) числа из набора задают суммы от 1 до (m - 1), и мы получаем тождество m(cnt + 1) = N + 1, то есть для m — делителя N + 1 — мы знаем, сколько раз его нужно взять, и получаем ответ d[m - 1] + cnt.
Теперь перебираем все делители N + 1 и находим ответ для d[N].
Если делать динамику вперед то она будет работать за n log n
Да, так еще лучше, спасибо.
В A ответ — обязательно множество делителей N, содержащих одинаковое количество множителей в разложении на простые. Пруфов не будет. Находим все делители N, группируем по количеству множителей, выбираем самую хорошую группу.
Более того, если все простые множители различны и всего их n штук, то самая хорошая группа — та, где каждый делитель — произведение n / 2 простых множителей, а если есть хотя бы один делитель, входящий в разложение в степени, большей 1, то работает следующее: найдём все делители из n / 2 простых множителей, теперь просто поделим каждое число на GCD всех. Полученное множество — оптимальный ответ.
Доказательство этого факта: пусть P — частично упорядоченное множество, r(x) — ранг элемента (т.е. r(минимальный_элемент) = 0), r(y) = r(x) + 1, если y непосредственно следует за x), Pi множество элементов ранга i. Пусть выполняются свойства:
1)
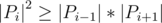
2)
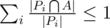, если A — множество несравнимых элементов (антицепь).
Теорема. Если выполняются эти свойства для множеств P и Q, то они будут выполняться и для P × Q (можно найти ее, например, тут, формулировка на стр. 6).
Далее будем рассматривать множество делителей, частично упорядоченное отношением делимости. Тогда ранг элемента равен сумме показателей степеней в разложении числа на простые множители.
Поскольку эти свойства справедливы для делителей числа, являющимся степенью простого, то, согласно этой теореме, они также будут справедливы и для множества всех делителей любого числа. Поэтому имеем:
Осталось доказать лексикографическую минимальность. Если A = Ps, то второе неравенство превращается в равенство. А это значит, что если мы возьмем в качестве ответа делители другого ранга, то выражение в левой части неравенства 2) станет больше единицы, что невозможно. Таким образом, любое наибольшее множество не делящихся друг на друга делителей содержит только делители ранга k, такие, что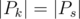
. Но поскольку s наименьшее из возможных, то любое другое множество, являющееся потенциальным ответом, будет содержать большие числа и, следовательно, будет лексикографически больше.
а как div2- E. Mobius band делается легко сможете сказать?
Ну там просто поиск в ширину, единственная сложность — понять, куда будет переход на краях.