Here is the editorial for Round #174. Thanks for participating. We hope you enjoyed the problems! :)

Div2 A

We didn’t expect this problem to be so hard :(. This problem can be solved by brute forcing. For any x,  you can compute 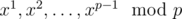in O(p) time (iteratively multiply cur = (cur * i) % p, not use pow in math library!), so overall brute force will be O(p²) time.

Note: there is actually 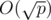algorithm.

The problem was written by abacadaea.

Div2 B

We first note that players who have folded do not affect our desired answer. Then, we can do casework on the number of players who are currently “IN”. If no cows are “IN”, then all the players who are “ALLIN” can show their hands. If exactly one cow is “IN”, she is the only one who can show, so the answer is 1. If two or more cows are “IN”, no one can show their hands. Then we simply count the number of cows of each type and check for each case. The total runtime is O(n).

The problem was written by scott_wu.

Div1 A / Div2 C Consider the problem with only queries 1 and 2. Then the problem is easy in O(n): keep track of the number of terms and the sum, and you can handle each query in O(1). But with query 3 we need to also be able to find the last term of the sequence at any given time. To do this, we keep track of the sequence d_i = a_i + 1 - a_i for i = 1, 2, ..., s - 1,  and a_s,  where s is the length of the sequence. Notice that query 2 only modifies one value of d_i,  and queries 1 and 3 are easily processed and able to update this information. This gives us an O(n) algorithm.

One can also use a fenwick or segment tree to compute the last element, but it’s not nearly as nice :).

The problem was written by abacadaea.

Div1 B / Div2 D

First, suppose we only have the sequence a₂, a₃, …a_n. We note that the current state is only determined by the location and the direction we are facing, so there are only 2·(n - 1) states total. Then, we can use DFS with memorization to find the distance traveled from each state, or  - 1 if a cycle is formed, in O(n) time. Now, when we add a₁ into the sequence, we essentially only need to give the distance traveled starting from each state facing left. The only difference is that if we ever land on a₁ again, there must be a cycle, as we started on a₁. Using this, we can solve the problem in O(n) time total.

The problem was written by scott_wu.

Div1 C / Div2 E

Imagine the problem as a graph where coins are the nodes and Bessie’s statements are directed edges between coins. Because of the problem conditions, the graph must be a set of cycles and directed paths. If there are any cycles in the graph, the answer is clearly 0.

Then, suppose we have a path p₁, p₂, …p_k in the graph, where it is known that we have more coins of type p₁ than of type p₂, more of type p₂ than of type p₃,  and so on. The key observation in this problem is that this is equivalent to having k independent coins of value {a(p₁), a(p₁) + a(p₂), a(p₁) + a(p₂) + a(p₃), …}. The first coin in our new list represents how many more coins of type p₁ than of type p₂ we have, the second coin in our new list represents how many more coins of type p₂ than of type p₃ we have, and so on. However, we must be careful to note that we need at least one of each of the new coins except for the last one, so we can subtract their values from T before doing the DP.

After creating our new set of values, we can run the DP the same way we would run a standard knapsack. This algorithm takes O(nt) time total.

The problem was written by scott_wu.

Div1 D

Let ν₂(n) denote the exponent of the largest power of 2 that divides n. For example ν₂(5) = 0, ν₂(96) = 5. Let f(n) denote the largest odd factor of n.

We can show that for fixed a_i, a_j(i < j),  we can construct a cool sequence a_i = b_i, b_i + 1, ... b_j - 1, b_j = a_j if and only if 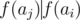and either ν₂(a_i) + j - i = ν₂(a_j) or ν₂(a_j) ≤ j - i - 1. Proof here

With this observation, we can use dynamic programming where the kth state is the maximum number of a_i (i ≤ k) we can keep so that it is possible to make a₁, ... a_k cool. The transition for this is O(n),  and the answer is just n - max (dp[1], dp[2], ..., dp[n]). This algorithm is O(n²).

The problem was written by scott_wu.

Div1 E

This will go over the basic outline for solution.

We can show that the answer is 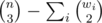where w_i is the number of wins cow i appears to have. Proof here

Now sort the skill levels of the cows (the order of the s_i doesn’t actually matter). s₁ is lowest skill. Now consider an n × n grid where the ith row and jth column of the grid is a 1 if the match between cow i and cow j is flipped. The grid is initially all zeros and Farmer John’s query simply flips a rectangle of the form [a, b] × [a, b].

We can process these queries and compute the number of wins for each cow using a vertical sweep line on the grid and updating with a seg tree on the interval [1,n]. The seg tree needs to handle queries of the form \begin{enumerate} \item Flip all numbers (0->1, 1->0) in a range [a, b]. \item Query number of 1’s in a range [a, b]. \end{enumerate} Note that given this seg tree we can compute the number of wins for each cow at every point in the sweep line as (Number of 1’s in range [1,i — 1]) + (Number of 0’s in range [i + 1, n]). There are O(m) queries so this solution takes 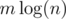time.

The problem was written by abacadaea.