I am attaching a picture about the question. Kindly refer to the picture. 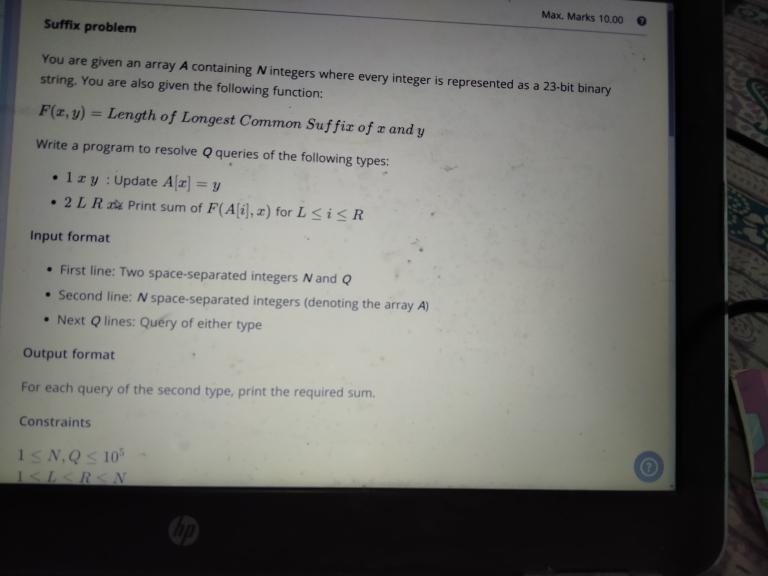
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
30:49:00
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
30:49:00
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 10:46:00 (j1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










Sample test cases?
You didn't tell us whether the test is finished or not. We shouldn't help you if the test is not finished yet.
It's finished bro.
Reverse all strings, so task becomes about prefix instead of suffix. Create segment tree, where each node have a trie that contains all strings from this node's corresponding segment (each string will be in $$$log~n$$$ tries, so memory will be $$$23 \cdot n~log~n$$$). With trie it's easy to count necessary sum of all string nested in this trie in $$$O(23)$$$, so overall query's complexity will be $$$O(23 \cdot log~n)$$$.
You can do it with a single trie
can you please explain
Basically what you and lemelisk said in the comment below, I'm not sure if it's better, just seems slightly easier to implement
create a trie with reversed strings and store indices of strings in each node in sorted order then query for reversed string, you can find out for each each prefix of reversed string how many strings from given range match this prefix
For updates you will need to store indices in BSTs that supports query "how many elements is smaller than given value". But that a nice alternative to segment tree's solution and it even has lower memory consumption complexity.
I solved it using map and policy based data structure My solution