Вступление
Задача меня порадовала (часть про [1...k], разумеется), на самом контесте я написал двухмерную динамику 3458123, но ограничения позволяли написать что угодно :)
Слышал я о решении полным перебором за kk + 2. Но после контеста я узнал о волшебной формуле ans = kk - 1
Поначалу не верилось, что это так. Но потом лень была побеждена, я взял тетрадку и ручку и начал считать свою динамику. Формула была выведена, но не очень-то быстро и красиво.
А теперь о причине, побудившей меня написать это: лично я понятия не имел (и не имею) о том, что такое Cayley trees. Поэтому хочу постараться подробно описать вывод формулы, не требующий никаких знаний.
Надеюсь, вы найдете у меня ошибку ;)
Динамика
Начнем с попытки прогенерировать первые номера домов.
Номер первого дома может быть любым от 1 до k, т.к. нам все равно придется искать путь из дома с этим номером в первый.
Условно обозначим это 1... (потом станет понятнее, почему обозначение именно такое), соответствующих вариантов у нас k.
Для номера второго дома есть три принципиально различных варианта:
- усл.об. — 11..., вариантов — k*1=k
-
- Но тогда мы не сможем попасть к первому дому от второго.
3 и более. Кол-во вариантов — k*(k-2). усл.об. — 13... Почему именно 3 ? Потому что если не 3, то мы вполне можем поменять местами дома так, чтобы этот стал третьим.
Переходим к третьему дому от первого варианта:
- 1 или 2. вариантов — k*2=2k. усл.об. — 111... Вот тут важный момент. Почему 112 не отличается от 111 ? Потому что и так, и так мы сможем дойти от всех домов к первому. Таким образом, '1' в усл.об. характеризует то, что от данного дома мы уже можем добраться до первого, а значит теперь необязательно стремиться в первый дом, можно стремиться в один из них.
... (дальше понятно)
Тогда посчитаем такую двухмерную динамику: в dp[x,y] будем хранить кол-во вариантов таких, что "обработано" уже х домов, причем из первых y из них мы можем попасть в первый. Из попыток генерации вполне понятно, как пересчитывать:
dp[1,1]=k
(j<i) dp[i, j] = dp[i - 1, j]·(k - i)
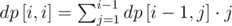
Ответом, очевидно, будет являться dp[k,k]
Вывод формулы
Путем анализа формул пересчета и божественного рандома заметим
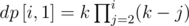
(i>1) dp[i, i] = ki - 1
(1<j<i) 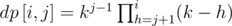
Теперь докажем эти формулы по индукции.
База индукции dp[1,1]=k верна.
(j<=i) 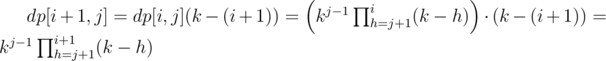
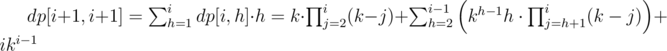
Для доказательства докажем индукцией по х такое равенство:
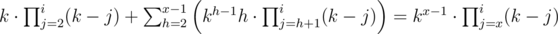
База индукции х=2, очевидно, верна.
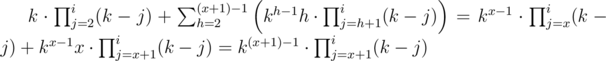
Подставляя в полученное равенство x=i, получаем
dp[i + 1, i + 1] = ki - 1(k - i) + ki - 1i = k(i + 1) - 1
Таким образом, формулы доказаны, а значит dp[k, k] = kk - 1 для всех k>1
Но так уж получилось, что 1 = 1^0, поэтому можно считать ответ всегда равным kk - 1










