Здравствуйте!
289A - Пингвин Поло и отрезки
Краткое описание. Есть 105 числовых отрезков, которые не пересекаются. За один шаг можно увеличить любой отрезок на 1 влево или вправо. Нужно найти минимальное количество шагов, после которых число целых чисел, принадлежащих отрезкам, будем делится на k.
Решение. Для начала нужно посчитать, сколько чисел изначально принадлежат заданным отрезкам. Поскольку они не пересекаются и даже не касаются (это следует из неравенства min(ri, rj) < max(li, lj) для всех i, j), никакая точка не может принадлежать двум отрезкам одновременно. Поэтому изначально величиной множества есть число 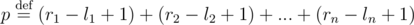 .
.
Если p делится на k, то ответом будет число 0 — не надо делать никаких шагов, все уже готово. Но если это не так, нужно подумать, за какое минимальное количество шагов из p можно сделать число, которое делится k. Можно увидеть, что за один шаг величину множества можно увеличить ровно на 1 (просто либо увеличив влево самый левый отрезок либо увеличив вправо самый правый), но на число больше 1 мы никогда его не увеличим. Тогда минимальное количество шагов будет равно минимальному числу t такому, что 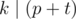 . Несложно убедится, что
. Несложно убедится, что 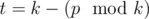 .
.
Примечание. Обратите внимание, что просто вывести 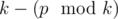 недостаточно: нужно отдельно рассмотреть случай когда
недостаточно: нужно отдельно рассмотреть случай когда 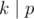 , или просто вывести
, или просто вывести 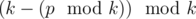 .
.
289B - Пингвин Поло и матрица
Краткое описание. Есть матрица n × m из целых чисел, а также число d. За один шаг можно увеличить или уменьшить любое из чисел матрицы (но только одно) ровно на d. Нужно найти минимальное количество шагов, после которых все элементы матрицы будут одинаковыми, или сообщить, что этого сделать невозможно.
Решение. Для начала нужно выяснить, когда не существует ответа. Для этого нужно заметить, что после выполнения операции над числом z величина 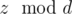 не изменится. Действительно
не изменится. Действительно 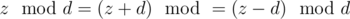 . Поэтому необходимым условием существования ответа есть условие, что все
. Поэтому необходимым условием существования ответа есть условие, что все 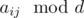 равны между собой. Несложно убедится, что это будет и достаточное условие (это также видно по алгоритму описанному ниже).
равны между собой. Несложно убедится, что это будет и достаточное условие (это также видно по алгоритму описанному ниже).
Теперь можно свести задачу к несколько другому виду. Переведем все n × m чисел матрицы в одномерный массив b, по сортируем по не убыванию и пронумеруем элементы от 1 до k (тут k это тоже самое что n × m). Цель задачи и шаги, естественно, остаются такими же. Несложно заметить в хотя бы в одному оптимальном ответе, все числа сведены к одному из чисел данного массива. Но, кроме этого, одним из оптимальных ответов будет свести все числа к числу 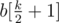 , то есть к медиане массива. Почему именно к медиане? Предположим, что свели не к медианному элементу с номером x. Тогда |x - (k - x)| > 1, то есть с одной стороны хотя бы на 2 элемента больше, чем с другой. Поэтому, передвинув число в сторону уменьшение абсолютной разницы, можно улучшить (или хотя-бы точно не уменьшить) результат.
, то есть к медиане массива. Почему именно к медиане? Предположим, что свели не к медианному элементу с номером x. Тогда |x - (k - x)| > 1, то есть с одной стороны хотя бы на 2 элемента больше, чем с другой. Поэтому, передвинув число в сторону уменьшение абсолютной разницы, можно улучшить (или хотя-бы точно не уменьшить) результат.
После того как известно, к какому число нужно свести, несложно понять что результатом будет сумма 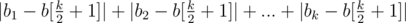 , разделенная на d.
, разделенная на d.
Сложность такого решения: 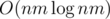 .
.
Примечание. Полным решением также является решение со сложностью O(n2m2).
288A - Пингвин Поло и строки
Краткое описание. Нужно построить лексикографически минимальную строку длины n, состоящую из ровно k различных маленький латинских символов такую, что-бы никакие два соседних числа не совпадали.
Решение. Решением этой задачи есть конструктивное построение нужной строки. Но для начала найдем такие параметры n и k, для которых не существует ответа. Естественно, что если k > n, то ответа не существует, так как не может быть k различных символов в строке длиной меньше k. Еще одним случаем есть случай когда k = 1, тогда если n > 1 ответа также не существует. Во всех остальных случаях ответ существует.
Теперь, когда мы знаем что ответ существует, нужно построить лексикографически минимальный. Предположим, что k = 2. Несложно понять, что оптимальным ответом здесь будет строка вида abababab.... Логично, что для k > 2 ответ будет точно лексикографически больше за ответ при k = 2, поэтому стоит как-то как можно правее что-то дописать к ответу для k = 2 так, что-бы он был ответом для k > 2. Минимальное что мы можем (и должны) сделать это переписать последние k - 2 символа строки на первые k - 2 символа алфавита, начиная с символа «c». Например, для n = 7, k = 4 у нас получается строка abababa, а после замены — ababacd.
Примечание. Не достаточно двух проверок k > n или k = 1, потому что для n = k = 1 есть ответ.
288B - Пингвин Поло и дома
Краткое описание. Нужно найти количество таких таких массивов p длины n из целых чисел от 1 до n, что-бы из первых k элементов можно дойти переходами вида x → px до 1, из последних n - k не можно было дойти до 1 и что-бы 1 был в цикле (т. е. можно дойти из 1 в 1 за положительное количество переходов).
Решение. Поскольку k ≤ 8, задачу можно решить перебором. То есть, нужно рекурсивно найти всевозможные варианты первых k чисел на табличках (очевидно, что все они будут в диапазоне 1..k). Всего таких вариантов будет kk (при k = 8 это число равно 16 777 216). Также, для каждого варианта нужно убедится, что он правильный, то есть удовлетворяет все три условия. Это несложно сделать циклом: просто пройтись по всем переходам пока не зашли в цикл и убедится что дом номер 1 был посещен через ненулевое количество переходов.
Когда количество вариантов записи первых k найдены (пусть оно равно f(k)), осталось только найти количество вариантов табличек для остальных n - k домов. Поскольку не должно существовать пути из них в 1, то не должно и существовать пути из них в любую из вершин с номером не больше k (иначе за первым условием будет путь в 1). Из этого следует, что на табличках домов с номерами от k + 1 до n можно ставить только номера от k + 1 до n. Так как нас не интересует как именно они расставлены, всего таких вариантов будет (n - k)n - k. Поэтому ответом будет f(k)(n - k)n - k.
Примечание. Существует также решение с использованием динамического программирование, а также более аналитическое — формула для f(k). Более подробно об этом обсуждалось здесь, здесь и здесь.
288C - Пингвин Поло и операция XOR
Краткое описание. Нужно найти такую перестановку p чисел от 0 до n, для которой величина 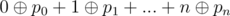 максимально возможная.
максимально возможная.
Решение. Так как нужно максимизировать ответ, нужно найти такую перестановку, при которой минимальное количество битов пропадут при операции xor, то есть что-бы было как можно меньше таких битов, что они одновременно равны 1 и в i и в pi (потому что тогда ои ничего не прибавят к ответу). Оказывается, для любого n можно найти такую перестановку, при которой ни один бит не пропадет. Как именно строить такую перестановку? Будем решать задачу итерациями пока n > 0. На каждой итерации, найдем самый старший бит, который не равен 0 в двоичной записи n и обозначим его номер (при нумерации с права налево от 0) через b. Также нужно найти число m — минимальное число от 0 до n (включительно), в котором бит с номером b равен 1. После этого можно увидеть (смотри рисунок ниже), что при 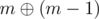 не пропадет ни один бит, при
не пропадет ни один бит, при  не пропадет ни один бит, ..., при
не пропадет ни один бит, ..., при 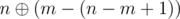 не пропадет ни один бит. Поэтому, нам стоит именное такие числа присвоить перестановке (то есть pm = m - 1 и pm - 1 = m, pm + 1 = m - 2 и pm - 2 = m + 1 и так далее). После этого присвоим n значение m - (n - m + 1) - 1 и перейдем к следующей итерации.
не пропадет ни один бит. Поэтому, нам стоит именное такие числа присвоить перестановке (то есть pm = m - 1 и pm - 1 = m, pm + 1 = m - 2 и pm - 2 = m + 1 и так далее). После этого присвоим n значение m - (n - m + 1) - 1 и перейдем к следующей итерации.

Теперь, когда известно как можно построить перестановку так, что-бы ни один бит не пропадал, ответом будет 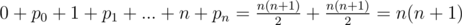 .
.
Примечание. В этой задачи было полезно написать генератор для небольших n. После этого несложно увидеть закономерность ответа, после чего намного проще дойти до его конструкции.
288D - Пингвин Поло и дерево
Краткое описание. Нужно найти количество пар путей в дереве, которые не пересекаются по вершинам (то есть не имеют общих вершин).
Решение. Как всегда в подобных задачах, подвесим дерево за какую-то вершину, например за вершину с номером 1. Нужно выяснить, что будет, если есть какой-то фиксированный путь и надо найти количество способов выбрать другой. Очевидно, что после удаления всех вершин этого пути и инцидентных к ним ребер, дерево распадется на лес (тоесть на множество отдельных деревьев). Пусть их размеры (количество вершин) это числа c1, c2, ..., ck, где k — их количество. Тогда нам с каждой из таких групп нужно выбрать пару чисел, то есть суммарное количество способов будет 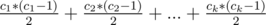 . То есть, если перебирать такие пути, достаточно воспользоватся этой формулой что-бы найти ответ. Но такой алгоритм — O(n2), поскольку нужно перебирать все пути. Нужно избавится от этого. Для этого dfs-ом обойдем граф и будем фиксировать одну из вершин пути (последнюю). Теперь нужно найти для всех других вершин сумму таких формул как описано выше. Можно здесь отдельно искать такое количество для вершин поддерева и остальных вершин (тех что первое ребро ведет вверх). Для вершин поддерева нужно делать следующим образом. Пусть у нас есть посчитаны ответы для всех вершин, в которые ведут ребра из текущей. Рассмотрим одну из этих вершин и прибавим к нашему ответу ответ из этой вершины. Но это еще не все — нужно добавить еще сумму всех
. То есть, если перебирать такие пути, достаточно воспользоватся этой формулой что-бы найти ответ. Но такой алгоритм — O(n2), поскольку нужно перебирать все пути. Нужно избавится от этого. Для этого dfs-ом обойдем граф и будем фиксировать одну из вершин пути (последнюю). Теперь нужно найти для всех других вершин сумму таких формул как описано выше. Можно здесь отдельно искать такое количество для вершин поддерева и остальных вершин (тех что первое ребро ведет вверх). Для вершин поддерева нужно делать следующим образом. Пусть у нас есть посчитаны ответы для всех вершин, в которые ведут ребра из текущей. Рассмотрим одну из этих вершин и прибавим к нашему ответу ответ из этой вершины. Но это еще не все — нужно добавить еще сумму всех 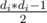 по всем другим вершинам что выходят из текущей (но кроме той которой мы рассматриваем), умноженное на количество вершин поддерева (не всего текущего, а только того что выходит из ребра что перебираем). Это удобно реализуется, используя частичные суммы для оптимизации (что-бы все время не пересчитывать сумму). Для остальных вершин (тех что не в поддереве) все аналогично, но немножко сложнее. Тут можно, например, в dfs-е поддерживать параметр, который равен ответу для текущей вершины. Потом, когда по ребру спускаемся вниз по дереву, нужно обновить результат как это было и в первом случае, но уже с количество вершин равным n минус размер поддерева (тоесть те вершины что не в поддереве).
по всем другим вершинам что выходят из текущей (но кроме той которой мы рассматриваем), умноженное на количество вершин поддерева (не всего текущего, а только того что выходит из ребра что перебираем). Это удобно реализуется, используя частичные суммы для оптимизации (что-бы все время не пересчитывать сумму). Для остальных вершин (тех что не в поддереве) все аналогично, но немножко сложнее. Тут можно, например, в dfs-е поддерживать параметр, который равен ответу для текущей вершины. Потом, когда по ребру спускаемся вниз по дереву, нужно обновить результат как это было и в первом случае, но уже с количество вершин равным n минус размер поддерева (тоесть те вершины что не в поддереве).
Примечание. Как вариант, можно искать количество плохих путей и выводить количество всех минус это количество. Еще возможным решением есть принцип разделяй и властвуй.
288E - Пингвин Поло и счастливые числа
Краткое описание. Есть два больших счастливых числа одинаковой длины. Нужно найти сумму произведений соседних счастливых чисел, которые лежат между двумя заданными.
Решение. В данной задаче необходимо вывести довольно много формул, большинство из которых необходимы для оптимизации решение (например различные частичные суммы). В разборе приведена только общая идея авторского решение. Детали можно узнать посмотрев решения участников либо задав вопрос в комментариях ниже.
Обозначим через a1, a2, ..., an все счастливые числа промежутка. Сначала нужно сделать следующее сведение задачи. Пусть в нас есть зафиксированная цифра (pos, d), то есть позиция (разряд) pos (начиная с 0 с права налево) и значение d (4 или 7). Тогда, для всех чисел ai (1 ≤ i < n) таких что pos-я цифра равна d к ответу нужно добавить ai + 1 × d × 10pos. Теперь видно, что задача можно свести к следующей. Для каждой фиксированной цифры (pos, d) нужно найти сумму все ai таких, что ai - 1 на pos-й позиции имеет цифру d. Естественно, задачу можно решить отдельно для промежутка 1..l и 1..r, а потом отнять первое от второго — это и будет ответ.
Как искать такую сумму среди всех счастливых чисел такой-же длины как входное, но меньших за какое-то x? Опишем общую идею. Любое счастливое число (да и вообще любое) число, меньше за x будет сначала совпадать с ним, то есть иметь некоторый общий префикс, потом одна цифра станет меньше чем в x (то есть там где в x стоит 7 в новом числе стоит 4), а далее цифры будут располагаться произвольным образом. Таким образом, перебрав эту цифру, мы, учитывая произвольность остальных, можем, используя частичные суммы искать ответ для всех позиций и цифр.











289B - Пингвин Поло и матрица Если сортировать не полностью массив, а только относительно медианы (либо найти k-ую статистику), то алгоритм можно сделать за O(nm). Жаль, что O(n2m2) проходило.
Там же ограничение на a 10_^4_, так что можно подсчётом за O(n*m) отсортировать.
I think 288B - Пингвин Поло и дома could also solved in O(nm) by what Xellos said here.
Am I wrong ?
You are right.
Задача Е.
Почему это так?
Ну если ни один бит не пропадает, то i + p[i] == i ^ p[i]. Поэтому искомую функцию можно преобразовать в виде суммы, что, собственно, и сделал автор.
Потому что когда при ни одном из xor-ов не пропадает ни один бит, он превращается в обычную сумму. То есть получиться сумма всех чисел перестановки (1, 2, ..., n) и (p1, p2, ..., pn), что и равно этой формуле.
Who can translate it into English? Orz
I think google translate does it well , at least it helps me :)
But I admire that the original translation would be more helpful :)
In the problem "Polo The Penguin and Matrix", the following test case is missing: 1 7 4 1 5 9 13 16 17 18 Some of the accepted codes are giving wrong answer on the above test case.
Problem B. Polo the Penguin and Matrix can be easily solved using ternary search. Just make a vector.All elements of vector are multiple of d in increasing order.Then just run a ternary search on vector and check it. my submission: http://codeforces.net/contest/289/submission/14401995
In 288B - Пингвин Поло и дома, my O(log(n)) solution using the formula ans = kk - 1 * (n - k)n - k gave correct answers to all system tests.
Since I was thinking of that formula intuitively, can anyone give me an idea of how to mathematically prove it?
UPD: Nevermind, I've just looked deeper and found Swistakk's comment on the announcement.
Can someone explain Div1 E?
Another solution of Div.1 E(?)
Let $$$calc(x)$$$ be the answer of $$$[44444...44,x]$$$. Then $$$ans=calc(r)-calc(l)$$$
It's not hard to find that if we want to change $$$a_i$$$ into $$$a_{i+1}$$$, we need to change the first "4" from the back to the front into "7" (let's suppose it's the $$$i$$$-th digit), and $$$i+1$$$-th, $$$i+2$$$-th, ..., $$$n$$$-th digit into "4". For example, $$$47447747777 \to 47447774444$$$.
Enumerate the number of trailing "7"s of $$$a_i$$$, say, $$$cnt$$$. $$$a_i$$$ can be expressed as "$$$xxx...xx4777...77$$$", $$$a_{i+1}$$$ can be expressed as "$$$xxx...xx7444...44$$$". If we replace "xxx..xx" with a $$$n-cnt-1$$$-digit number $$$X$$$, and we call the number $$$777...77$$$ (there're $$$k$$$ 7s in it) $$$seven_k$$$, $$$444...44$$$ $$$four_k$$$, then $$$a_i=X\times 10^{cnt+1}+4\times 10^{cnt}+seven_k$$$, $$$a_{i+1}=X\times 10^{cnt+1}+7\times 10^{cnt}+four_k$$$.
$$$a_i a_{i+1}=(X \times 10^{cnt+1}+4\times 10^{cnt}+seven_k)(X \times 10^{cnt+1}+7 \times 10^{cnt}+seven_k)=X^2 \times 10^{2cnt+2}+7X \times 10^{2cnt+1}+X \times 10^{cnt+1} \times four_k+4X \times 10^{2cnt+1}+28 \times 10^{2cnt}+4 \times 10^{cnt} \times four_k+X \times 10^{cnt+1} \times seven_k+7 \times 10^{cnt} \times seven_k+seven_k \times four_k$$$
Let $$$S_i$$$ be all the $$$i$$$-digit lucky numbers less or equal than the first $$$i$$$ digits of $$$x$$$. $$$f_{i,0}=|S|,f_{i,1}=\sum_{i \in S}i,f_{i,2}=\sum{i \in S}i^2$$$. Replace $$$X,X^2$$$ with $$$f_{i,0},f_{i,1},f_{i,2}$$$ and calculate the fomula above. $$$f_{i,0},f_{i,1},f_{i,2}$$$ can be obtained by digit dp.
AC code: 95351065
I have already ACed this problem. Why are you so vegetable???
mol to show respect.
Problem B. Polo the Penguin and Matrix has got the tags of DP. Can someone share the dp solution?