Предлагаю обсуждать здесь задачи прошедшего Гран-При.
Вопрос: кто-нибудь умеет решать C? Мы её конечно сдали, но решать не умеем =) Загнали симплекс-метод.
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 03:02:58 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Как решать А?
За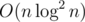
. Считаем для каждого отрезка самую левую и самую правую достижимые точки. Делаем это за log n итераций, на каждой итерации с помощью дерева интервалов удваиваем количество допустимых промежуточных отрезков.
деревом интервалов, сначала решаем задачу кто покрывается с помощью одного отскока, потом по полученным данным кто покрывается с двух отскоков, потом кто с 4, с 8 итд
Можно за O(NlogN) следующим образом. Отсортируем все бомбы по возрастанию икса и построим на них дерево отрезков. Под деревом отрезков здесь я подразумеваю не какую-то структуру данных, умеющую выполнять быстро некоторые операции, а просто ориентированный граф, у которого ребра направлены от корня вниз. Листьями будут сами бомбы.
Теперь, для каждой бомбы добавим ребра из нее во все бомбы, до которых достает ее взрыв. Для этого достаточно из нашей бомбы добавить O(logN) ребер в соответствующие вершины дерева отрезков. Получим граф, у которого O(N) вершин и O(NlogN) ребер. После этого, построим его конденсацию по компонентам сильной связности. Ясно, что внутри одной компоненты для всех бомб будет одинаковый ответ. В этом новом графе пройдем по всем вершинам в порядке топологической сортировки и найдем для каждой вершины левую и правую границы ее взрыва. Например, левая граница будет равна минимуму из того, что уже есть и наименьшей левой границы всех потомков данной вершины.
Когда мы для каждой бомбы нашли левую и правую границы ее взрыва (с учетом взрыва других бомб), можно найти для нее ответ за O(logN) бинпоиском в отсортированном массиве всех бомб.
Вообще мы какую-то ерунду затолкали по А. Сначала пройдёмся слева направо и используя значения бомб левее пересчитаем наиболее левую вызываюмую координату Потом наоборот пройдёмся слправа налево и используя значения бомб правее пересчитаем наиболее
левуюправую вызываюмую координату А затем просто для каждой банки пересчиаем ответ как левейшее и наиправейшее значение на отрезкесвоего радиусасвоей достижимости(левейшее и правейшее)UPD: упс, в одном слове ошибся. UPD2: выяснилось ещё одно обстоятельство: шаг 3 делается несколько раз пока он вносит изменения
Вот кто-то понимает почему это работает? Я уже мозг сломал)
Если я правильно поняла алгоритм, это не работает на примере (0, 1), (3, 2), (5, 1), (6, 6).
При взрыве второй бомбы взрывается третья бомба (которая правее), потом четвертая бомба (которая еще правее и имеет очень большой радиус поражения) и за счет нее — первая бомба (которая оказывается левой границей для второй бомбы). При проходе слева направо левые границы для второй и третьей бомб посчитаются неправильно. Их невозможно правильно посчитать, учитывая только бомбы левее. Теперь в отрезке радиуса второй бомбы находится только третья, для которой левая граница > 0, поэтому для второй мы получим неправильную левую границу.
Этот алгоритм работает правильно, если третий проход делать в порядке уменьшения радиуса.
На моем примере сначала ответ посчитается для четвертой бомбы, потом — для второй, которая задействует третью, у которой радиус меньше и ответ пока неправильный.
Первыми двумя проходами мы посчитаем, куда дойдет взрыв, если он будет идти только влево или только вправо, а третьим проходом мы берем минимум и максимум посчитанных значений на посчитанном отрезке (а не на отрезке одного нашего взрыва).
Все посчитается правильно
если правильный ответ (1, 3, 2, 4) то этот тест проходит.
при проходе слева направо получаем: (-1, 1, 4, 0) при проходе справа налево получим: (12, 12, 12, 1)
а дальше всё посчиается правильно
C — просто венгерка на матрице расстояний между точками, на диагоналях ставим бесконечности. Доказательство — имеется теорема, что max искомой суммы равен min(sum(A[i][j]*Coef[i][j])) при условии сумма коэффициентов в каждом столбце и строке не меньше 1. Паша заметил, что это также двойственная задача линейного программирования. Далее замечаем, что это ровно минкост, а т.к. пропускные способности целые, то это венгерка.
А что за теорема?
Ответ от минкоста нужно делить на 2 (чтобы с сэмплами сошлось и, кстати, почему?) или что-то хитрее делать?
А как там может проходить симплекс метод? там же на одну итерацию уходит O(n^4) операций. и итераций как минимум n. Да еще и мультитест
С чего бы n^4? Там матрица 1225x50.
Ну на сколько я знаю симплекс метод, он не работает с неравенствами. А значит придется добавить для каждого неравенства дополнительную переменную. Получается матрица 1225х1275
Нууу, это если совсем уж втупую писать. Если же обзавестись нормально написанным prewritten симплекс-методом, то поддерживается матрица именно 1225x50. В википедии вроде рассказывают, как это нормально реализовывать и какую матрицу поддерживать.
А можете для ознакомления поделиться нормально написанным симплекс-методом, пожалуйста?
Вот, например. Насколько понимаю, автор indy256.
Как В решать?
Так straight-forward поток же. Создаём h+1 копию поля, убираем плохие клетки, а остальные соединяем между слоями. Единственная проблема — на java-64 построение графа работает в 150 раз дольше чем поток и не укладывается в ТЛ :) На java-32 получается быстрее, но построение графа всё равно сильно тормознее потока.
Стоп. Я не поняла, граф строить в явном виде надо или нет? просто строя его у меня ТЛ
сам поток диницем ищите?
да, правда я раздваивала вершины, возможно этого делать не стоило?
стоило, очень странно, что не заходит, каким образом граф храните? в смысле как память выделяется?
с начала пыталась векторами, поняла что медленно, потом выделяла статически уже где то 40*100*100 под два массива связанных с вершинами и еще 3 по столько же(были варианты и больше до этого, но все ТЛ) для ребер
Под вершины массив маловат. вершин же 2*25*100*100+2. Ну и под ребра может быть тоже больше, чем 3*количество вершин. А рантайм иногда влечет за собой ТЛ.
нашла ошибку, память не чистила в одном месте, но теперь ВА(
Мы строили явно граф и искали поток максимально тупо(dfs-ом ищем путь, добавляем его)
Да, строить граф в явном виде, это заходит. Сам поток после построения графа работает десятки миллисекунд, вся проблема в том, чтобы граф в память уложить. Вы под 32-битным компилятором отсылали или под 64-битным? Какой язык?
32, С++, а на что это влияет?
В джаве 32/64 влияет ну очень сильно, почему — не знаю, наверное, особенности сервера (ну либо приколы JVM). В C++ тоже имеет значение, т.к. это влияет на размер указателя.
На opencup.ru, кстати, есть подсказка о том, что 64-битную джаву не следует использовать:
Мы честно строили граф. Писали на Java, алгоритм Диница с емакса зашел сразу же, как поменяли
class Edgeна четыре массива.У нас вместо замены Edge на массивы был ресабмит под java-32. Видимо, в java-64 создание объектов ну очень дорогое.
Да, ТЛ в этой задаче и в J жесткач. В обоих нам пришло неасимптотически упихивать. Здесь зашло после того как перестали создавать объекты для рёбер (локально ускорилось с 8 до 5 секунд на тест).
Ты путаешь, это в j с 8 до 5 после замены хешмапы на сортировку
А, точно. А в этой с трех до одной.
Мы пытались сдать такое решение: Строим последовательные приближения радиусов, на каждом шаге увеличиваем сумму. Как устроен шаг: строим граф, вершины соединены ребром, если их радиусы в сумме равны расстоянию между точками. Ищем в этом графе независимое множество, которое больше по размеру, чем количество их соседей. Все радиусы внутри этого множества увеличиваем, у соседей уменьшаем.
Ахахахахха, изобретатели велосипеда))) Ренат, а вот часть увеличиваем внутри множества и уменьшаем у соседей тебе ну совсем ничего не напомнила?
Идея, что тут может быть поток у меня возникала 100-500 раз, но ни разу я так и не смог ее к потоку свести.
Нет, я скорее имел ввиду шаг увеличение/уменьшение на множестве, это же основная итерация венгерского алгоритма.
к венгерке я тоже не смог свести, хотя конечно стоило загнать не разбираясь
Как J решать за приемлемое время? Есть ли решение на Java, может кто-нибудь поделиться?
Идея в том, чтобы от ребёнка к родителю переходить за O(1).
Более подробно: ответ для родителя получается из ответов для детей дописыванием к ним всем в начало 1, если они все разные. Если есть k одинаковых, то к одному нужно дописать 1, ко второму 2, и так далее, к последнему k. Если последовательность заранее сделать нужного размера, то дописывать в начало можно не сдвигая; чтобы быстро искать одинаковые, будем поддерживать хэш, и при дописывании числа быстро его пересчитывать.
(Это всё придумал Egor).
Да мы так и делали, обычная ситуация, цвета не хватает. Хочу исходник, Egor же выложит его в свой репозиторий?
Код в истории правок.
Спасибо. Действительно неасимптотические оптимизации, например, мы сохраняли, как от одного хеша переходить к другому, и строили ответ уже после вызова dfs, и это почему-то сильно тормозило, хотя там суммарно порядка n2 действий...
На самом деле зашло после асимптотического ухудшения :). (Лишний лог засчет сортировки вмсето хеша)
У нас есть именно такая сортировка, дело в другом, просто в некоторых местах мы создавали разнообразные структуры данных, от которых вы успешно избавились. А кто-нибудь знает, какой TL на сервере? У меня на чуть худшем компьютере около 7 секунд работает.
Какое-то у вас сложное решение.
То, что ты написал, по сути доказывает, что размер ответа O(N). Воспользуемся этим фактом и тупо перечислим все ответы, проверяя каждый за O(N).
Как будем делать: пусть текущий ответ a1, a2, ..., ak - 1, ak, 0. Проверим его. Если подходит, перейдем к a1, a2, ..., ak - 1, ak, 1, 0, если нет, то к a1, a2, ..., ak - 1 + 1, 0.
Проверка за O(N) совсем простая: вершина на глубине i подходит под конструкцию ai, ..., ak, 0, если подходит хотя бы ai её сыновей под конструкцию ai + 1, ..., ak, 0.
А как быстро проверять, подходят ли хотя бы ai сыновей под ai+1,...,ak,0?
А, кажется понял, всё втупую делается. Прикольно! У нас получается что-то типа O(n*высоту дерева), но это от твоего O(n^2) не отличается, так как высота не ограничена.
Как решать G и H?
G очень просто решать, когда запросов на изменение веса ребра нет — тогда нужно отсортировать все ребра по убыванию веса и по очереди добавлять в граф, попутно для очередного веса отвечая на все запросы о существовании пути из A в B. Так как в этой задаче веса ребер менялись не более 2000 раз, ты мы разбили все запросы во входных данных на группы, в каждой из которых не происходит изменений весов, для каждой группы решали отдельно описанным подходом.
Вообще говоря это e' — кол-во запросов изменения умноженное на M * alpha. Для одного теста должно работать хорошо, а вот на мультитесте непонятно. Вам пришлось пихать?
Если все сдали это, то обидно, мы потратили время чтобы улучшить с e' * M * alpha до e' * (N + e') * alpha + e, воспользовавшись идеей что достаточно оставить оставить только те ребра которые где-то в запросах меняются и те, которые войдут в остовный лес если удалить все ребра которые где то меняются. Таким образом на каждом шаге обрабатываем не M, а только e' + N ребер.
Не, просто заслали и сдали с плюса:) Поначалу думали, что надо как-то использовать небольшое ограничение на N, но не успели придумать — задача сдалась.
По опыту прорешивания американских контестов, в них вообще редко что-то пихать приходится, тесты очень приятные.
По опыту прорешивания американских контестов, могу сказать что вам все-таки повезло)
Ну H вообще ни о чем — брать и строить таблицу истинности для каждого выражения. Она размером 2^20, нужно сжать побитово чтобы получилось 2^15 intов.
И с чего оно должно зайти? В каждом выражении 128/2 = 64 логических операций, выражений ~5000, итого 5000 * 64 операций с битсетом на 2^20 элементов, т.е. 5000 * 64 * 2^15 = 10485760000, что, кажется, слишком много. А сколько у вас на макстесте работает?
Ну это же world finals style контест, макстеста может и (намеренно) не быть.
Мы писали из соображений "ну а как это еще в принципе можно было бы решать".
На макстесте на ноуте, работающем от батарейки, работает 55 секунд и ест 2 гига памяти.
На ноуте к тому же 64-битная джава.
Думаю на сервере это секунд 5-10.
А что плохого в 64-битной яве? Я всегда считал, что единственная причина, по которой на ней ничего не сдать — это тот факт, что в серверной jvm постоянно работает сборщик мусора, и процессорное время в проверяющей системе получается вдвое больше астрономического.
Ничего конкретного — просто эмпирически медленнее все время выходит.
А что у вас в этой задаче?
Может можно каким-нибудь ключом поменять поведение GC на более подходящее в нашем случае?
Может кто-нибудь подскажет, как решается задача Е о нахождении точки прокола прямоугольников.
Запишем координаты точки в новой системе координат и в старой. Приравняем их. А дальше у нас получается 2 уравнения с 2 неизвестными. Решаем эту систему.
проше в комплексных числах:
далее два варианта, либо просто много раз прыгаем итеративно начиная с произвольной точки:
либо просто решаем уравнение:
и сразу получаем неподвижную точку:
А можно взглянуть на Ваш код sdryapko. Спасибо.
Его код под правкой. Надеюсь, с авторскими правами проблем не будет)
А еще можно применить операцию 2000 раз. Это будет работать, т.к. 0.992000 это достаточно мало.
А как правильно написать I за 4 — 20 минут ?
Хешами и бинпоиском :)
Два вопроса :
1/
2/ более похоже на правду
А как D решалась ?
Мы писали max-flow min-cost, некоторые Венгерский алгоритм(тут по сути одно и то же). Понимаете как их сюда использовать?
а мы писали и то и то, но минкост не прошёл :(
А чем писали поиск пути? Дейкстра с потенциалами за O(M logN) зашла на яве спокойно без оптимизаций
вставлял провереный минкост через дейкстру с потенциалами. не проходило из-за WA. может бага в самом графе? из истока m рёбер (1,0), от студентов рёбра (1, 12-*ЧислоИзТаблицы*), от кафедр в сток рёбра (p[i], 0). ответ 12*m-cost.
P.S. код был вроде проверен только на этой задаче.
p.p.s. нашёл две эпичных ошибки в коде. никогда не тестируйте свой минкост на задаче выше по ссылке.
Странно, может и правда в графе ошибка. Мы сдали дейкстру, граф строили также, только от студентов ребра (1, -ЧислоИзТаблицы). Ответ просто -cost.
мы писали Левита ( как на e-maxx ) прошло на с++ спокойно без оптимизаций :)
У нас минкост тоже не зашел, когда я решил перестраховаться и добавлял не 4 ребра из человека, а все ребра(думал, что, мол, могло так оказаться, что в некоторых случаях если мы берем работников только на их приоритетные специальности, то можно было взять не так много людей, но обеспечить при этом mincost). Это действительно ТЛится. Не совершили ли вы такой же ошибки?
сейчас нашёл багу — не отчищал один массив. стало ТЛится, но добавляю лишь по 4 ребра.
Можешь код куда-нибудь выложить? Наверняка бага в реализации.
да, вот