Уважаемые организаторы, не получается взять условия из системы.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:19:03
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:19:03
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 10:15:58 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Это и есть условие первой задачи.
Похоже на еще один условно внезачетный
http://acm.spbgu.ru/divone-e.pdf http://acm.spbgu.ru/divone-r.pdf http://acm.spbgu.ru/divtwo-e.pdf http://acm.spbgu.ru/divtwo-r.pdf
Как решать D? Если A == D, B == E, C == F, то вроде есть явная формула; иначе мы не придумали ничего умнее, чем использовать алгоритм для количества полных паросочетаний в планарном графе; но там в конце надо извлечь квадратный корень из определителя, из-за чего Гаусса приходится делать в BigInteger'ах, а это адски долго.
Если противоположные стороны не равны, то ответ -- 0 :)
Вротмненоги!!11 Я ведь хотел попробовать такое заслать, перед тем как решение для планарных графов писать :( Но был переубеждён правдоподобным утвержнением про то, что 0 только при A + B + C + D + E + F mod 2 = 1.
Если раскрасить треугольники в шахматном порядке и построить матрицу смежности между треугольниками разного цвета, то ответ — определитель с точностью до знака.
Хм, а почему это так? Казалось бы, должен быть перманент, а не определитель...
В пространстве циклов этого графа можно взять базис с циклами длины 3, поэтому, казалось бы, любое паросочетание из текущего можно получить элементарными заменами по циклам длины 3, поэтому все ненулевые слагаемые в перманенте будут одного знака => модуль определителя равен модулю перманента. А знак можно определить по паросочетанию, найденному Куном.
Разве там есть хоть один цикл длины 3?
Да, действительно). Будем считать длину цикла как количество вершин одной доли в этом цикле.
А, я понял ваше решение, спасибо. Правда в терминах перестановок имхо понятнее, чем с циклами
Можно рассмотреть замощение, как какую-то фигуру в параллелепипеде AxBxC. Фигура представляет из себя A лесенок размера не больше BxC, где каждая последующая лесенка не превосходит предыдущую. Количество таких фигур — количество различных комбинаций непересекающихся путей с нижней стороны на верхнюю. Оно ищется через определитель вот так: http://en.wikipedia.org/wiki/Lindstr%C3%B6m%E2%80%93Gessel%E2%80%93Viennot_lemma. Количество путей в параллелограмме AxB равно C(A+B, B). Итоговое решение: определитель матрицы размера AxA, где Xij = C((b+i-j)+(c-i+j), (b+i-j)) = C(b+c, b+i-j).
Как решать E? Писали min-cost-flow c кучей оптимизаций, TL 28.
С чего бы ему зайти, на таких-то ограничениях? Честное решение гораздо прикольнее.
Делаем так:
1) Забьём на веса на правой доле, найдём оптимум в левой доле (легко доказать, что это то же самое, что и лексикографический оптимум)
2) То же самое симметрично
3) Получили 2 подмножества вершин — слева и справа. Выбросим всё кроме них, найдём полное паросочетание в полученном графе (можно доказать, что оно всегда найдётся). Это и есть ответ.
Интересно, проходила ли в этой задаче венгерка за (номинально) четвертую степень.
Было бы очень странно, если бы прошла. И даже за куб — было бы очень странно.
В любом случае, загонять такое неинтересно — специально же дали непроизвольные веса, значит, жюри должно было постараться, чтобы решения для произвольных весов не прошли.
Минкост протолкали, а есть инфа, что венгерка за куб быстрее.
Жаль, надо было более жёсткие ограничения делать.
У нас Sfairat написал Венгерку — тлешится
Про скорость работы:
Найти mincost/maxcost паросочетание в двудольном графе с произвольными весами можно с помощью
На произвольном графе Венгерка рулит так, как константа мала (в 4-8 раз быстрее Дейкстры).
На случайных/спецэффических разреженных (V ~ E) графах рулит Форд-Беллман с очередью, так как фактически каждый путь ищет за O(E). А вот Дейкстра и Венгерка вообще не рулят так как их VElogV и V3 достигаются.
В данной задаче никакой из этих трех методов проходить не должен был. Сложнее всего (что логично) было завалить Форд-Беллмана, об этом я сейчас в соседнем комментарии напишу подробнее.
Минкост с дейкстрой как-то зашел :)
В задаче E со вчерашнего контеста? а можно код посмотреть? :)
У нас на контесте зашел обычный min-cost-flow, вот код: http://pastebin.com/ZqWxTu75 В дорешке только вот он не заходит ).
Чудеса да и только! А мы, увидев ваш AC на 34ой минуте, долго придумывали очевидную жадность или что-то похожее, что можно быстро закодить. Сбили людей с толку:)
Форд-Беллман с очередью, конечно, проходить не должен был =( На момент начала контеста все мои честные реализации min cost flow на cpp работали >15 секунд.
Фишка в том, что у вас сеть имеет веса (0; w1+w2; 0), а когда я строил тесты специально против Форд-Беллмана, я сперва завалил сеть с весами (w1; 0; w2), а про вашу подумал "эта еще хуже". Нужно было быть внимательней =(
Вот вам на память тест, на котором ваш код "висит" (как и положено, работает больше 15 секунд). Этот тест добавится в архив, rejudge-ить, конечно, уже поздно :-)
Мы сдали такое решение: сортируем первую долю и делаем обычного Куна, только каждый раз при обходе в глубину выбираем удлиняющий путь заканчивающийся вершиной второй доли с наибольшим весом.
Как решать A?
Мы сделали так: сведём задачу к CSP. Дальше заметим, что CSP таких размерностей можно решать рандомизированно, просто перебирая клаузы и рандомно меняя переменные, если клауза не выполнена. Вроде получается доказать, что итераций надо мало. Мы такую задачу для SAT уже давали в ПЗ на Unpredictable Contest 3 (задача C), но с раскрасками графа конечно прикольнее.
Степень любой вершины не превышает три. Для каждой компоненты связности выберем вершину, покрасим ребра из нее рандомно. Рассматриваиваем на каждой итерации вершину, одно из ребер которой уже определено. Если из нее есть еще одно ребро, то для него не более двух вариантов (цвета 1 и 2), если два ребра — тоже не более двух вариантов (пара 1,2 и пара 2,1)
Хм, а мы просто перебирали рёбра одного цвета, а остаток красили в два других поиском в ширину. Отсечение: степень каждой вершины в остаточном графе меньше трёх.
А кто-нибудь сдал такое очевидное решение по А — покрасить ребра из какой-то вершины в 3 цвета, а дальше пустить из нее dfs и на каждом шаге перебирать 2 варианта покраски? Получается асимптотика O(2n * m), но что-то не верится, что это зайдет.
Мы это и сдали :) Не очень понятно, откуда множитель "m" берётся, так как из каждой вершины у нас будет не более трёх рёбер выходить же.
Опровергните кто-нибудь идею по Е. Посмотрим как будет работать min-cost (max-cost). Он будет все время искать в графе путь из истока в сток максимальной длины. Он найдет удлиняющую цепь в двудольном графе, которая начинается в вершине v1 и заканчивается в v2 + ребро из истока и ребро в сток. Собственно, для этой задачи все ребра, кроме ребер из истока и в сток нулевые. Тогда отсортируем все пары вершин, первая из первой доли, вторая из второй, отсортируем их по убыванию суммы весов. Потом будем в этом порядке искать удлиняющую цепь начинающуюся в в вершине из первой доли и заканчивающуюся в вершине второй доле (из текущей пары). Если хотя бы одна из вершин пары уже покрыта паросочетанием, не будем ничего делать. Казалось бы, минкост будет делать то же самое. Но наше решение упорно получало ВА4. Кто-нибудь может найти ошибку или у нас таки бага?
Я не знаю, на сколько это поможет, но у нас была проблема с кратными ребрами. Выводились все сразу. Например
То есть, вы это сдали?
Ну не на 100% это. Сдали такое: будем перебирать вершины левой доли по невозрастанию стоимости. Для каждой вершины находили самую дорогую, которую можно включить в парасочетание. Вот это зашло.
P.S. я тест поправил. была опечатка
Да, не работает, спасибо.
Кратные рёбра?? Кратные рёбра!!! 2 долбанных часа я искал ошибку в реализации, а тут кратные рёбра))
Поздравляю ИТМО 1 с досрочной победой в общем зачете
Спасибо. Только я тут подумал, если будет еще один условно внезачетный и вы оба Гран-при выиграете, тогда вы нас догоните :)
Это надо 2 условно внезачетных, потому что у нас нету второго места
UPD: хотя нет, 4 * 100 + 60 == 3 * 100 + 2 * 80, да
Это не очень важно, конечно, но я перепроверил, вроде бы вот так:
У нас: 100+80+100+80+80+100+0+0-(0+0+80)=460
У вас: 32+60+50+100+100+60+100+100-(32+50+60)=460
что написали итмо1 в G за такое малое время?
Спроси у Moscow SU Trinity, они должны быть в курсе.
просто итмо до G написало B за 15 минут, либо просто G, получили ва и Б... вообщем, в любом случае быстро 3 задачи
Я написал решение за O(2^k*n*logn) — перебираем все маски, по которым будет в итоге происходить совпадение, хешируем в каждой строке символы, попавшие на эту маску, разбиваем сортировкой на группы с равными хэшами, если в группе больше одной строки с таким хэшом, то релаксируем для этих строчек ответ (их можно поставить в соответствие друг другу). Бревно из-за неправильно подключенных файлов :-( Пишется минут за десять.
What is the 44th test in Div2 T like?
It's like
2, 2; 4, 4; 6, 6; ... 96, 96; 98, 98; 99; 100shuffled randomly, and the answer is -1. The basic idea was to have almost all powers (but not all of them) have the same residue modulo some small number.Я хотел бы, как автор задач A, E, G и H, поделиться некоторыми мыслями/решениями. Если какие-то мысли уже были озвучены, для полноты картины я их приведу еще раз.
0. Все мои решения укладываются в TL >= 4 раз.
1. Задача G.
В задаче G подразумевалось решение за время O(2k n). Если вы писали решение за O(2k nk), оно могло получить TL (зависит от оптимальности кода).
Одно из решений за O(2k n): рекурсивно перебираем 2k масок "какие символы совпали", в рекурсии на каждом шаге за O(n) пересчитываем хэши n подпоследовательностей и в конце за O(n) с помощью хэш-таблицы проверяем, какие хэши встречаются хотя бы дважды.
2. Задача A
В задаче A я знаю 2 решения. Оба пользуются мыслью, что в графе нет вершин степени больше 3 (иначе ответ — NO).
Первое за O(2n). По сути то же, что и писал I_love_natalia здесь. Красим компоненты связности не зависимо; пусть граф связен; взяли произвольную вершину v; покрасили ребра, выходящие из v, в произвольные различные цвета; обойдем граф dfs-ом из v; когда мы входим в вершину x, всегда одно из смежных x ребер уже покрашено, покрасить остальные смежные x ребра можно не более чем двумя способами, переберем оба способа. Для этого решения есть мощная оптимизация, после которой оно начинает "летать": при покраске в ровно 3 цвета заметим, что если у какого-то ребра не более двух соседей, можно это ребро выкинуть из графа, покрасить оставшуюся часть графа, а в конце покрасить это ребро в оставшийся третий цвет. Будем выкидывать так ребра, пока можем. От этого граф стал более насыщенным, многие варианты покраски будут сразу отметаться.
Второе за O(3n / 2 m): пока в графе есть вершина степени 3, берем ее и перебираем, какое из трех смежных с ней ребер мы покрасим в цвет 1. Покрасив ребро в цвет 1, помечаем его "уже покрашенным" и уменьшаем степени концов. Таким образом есть всего 3n / 2 вариантов свести задачу к случаю "степени всех вершин не больше двух", а это набор путей и циклов, которые можно раскрасить жадно. Всё кроме нечетных циклов красится в 2 новых цвета. В нечетном цикле нужно одно ребро покрасить в цвет 1, проверим, есть ли такое.
3. Задача H
Для начала можно развернуть карту по x и по y так, чтобы идти нужно было только в направлении x++ и y++.
Теперь решение — посчитать динамику f[x,y] = сколько времени займет от точки (x,y) дойти до конца. Зная f[x+1,y] и f[x+2,y] и f[x+1,y+1] и f[x,y+1] и f[x,y+2] легко посчитать f[x,y]. Для этого нужно разобрать несколько случаев и посчитать интеграл от 0 до 2t от кусочно линейной функции f(w). Один из способов посчитать интеграл следующий: разбиваем 0..2t на промежутки 0..t-s..t..2t-s..2t, на каждом отрезке f(w) устроена как min(const1, const2 — w). Берем точку излома, делим промежуток еще на два, интегрируем линейную функцию.
4. Задача E
Для задачи E мне известны 3 решения, все за O(VE).
Первое через min cost flow. Похоже на то, что описал tunyash здесь. Есть двудольный граф + исток + сток, веса из истока = w1, веса между долями = 0, веса в сток = w2. Ищем максимальный по весу путь из истока в сток. Он имеет вид "первое ребро — много нулей — последнее ребро". Итого, чтобы максимизировать вес пути, достаточно сделать следующее: переберем вершины первой доли в порядке убывания веса, если мы в вершине еще не были, запустим из нее dfs "по нулевым ребрам". При этом для каждой вершины второй доли мы нашли максимальную по весу вершину первой, от которой существует путь (это та вершина первой доли, из которой мы пришли dfs-ом). Выберем вершину второй доли такую, что "ее вес + вес ее потенциальной пары" максимален, они и образуют дополняющий путь.
Второе такое (его, например, сдала команда SPB Angry Muffin): сперва максимизируем сумму весов в первой доле. Это делается так: сортируем по убыванию веса и в таком порядке ищем дополняющие пути Куном. Теперь рассмотрим два паросочетания: текущее и оптимальное. Рассмотрим их симметрическую разность. Поймем, что нечетных путей быть не может, четные циклы нам не интересны, четные пути начинающиеся и заканчивающиеся в первой доли нам тоже не интересны. Остаются четные пути, начинающиеся и заканчивающиеся во второй доли, улучшающие ответ. Будем их искать следующим образом: отсортируем вершины второй доли по убывания веса и в таком порядке будем запускать dfs-ы, которые ищут дополняющие чередующие пути четной длины (поменять одну вершину 2-й доли, на вершину 2-й доли с большим весом).
Третье описал ilyakor здесь. Кстати, интересно по поводу "можно доказать, что оно всегда найдётся"... Это возможно доказать без матроидов? Например, если веса только в одной доле, очевидно, что жадность работает "потому что min cost flow".
Мы на контесте это разумеется не делали, но наверняка каким-нибудь ad-hoc'ом можно, надо подумать.
По поводу A — выяснилось, что наше решение доказуемо работает за 1.5n·m (а точнее — если после 1.5^n итераций не нашлось ответа, то его вообще нет с вероятностью >= const). Так что асимптотически оно быстрее решений жюри (т.к. 1.5 <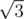 ), хоть и вероятностное.
), хоть и вероятностное.
Илья, а можешь подробнее описать ваше решение? Это что-то по типу того, что предлагает David Eppstein link?
В той статье всё сильно умнее, чем у нас. Мы делали примерно следующее:
1) Сводим задачу к CSP: переменные — цвета на рёбрах, клаузы — для каждой пары рёбер с общей вершиной цвета рёбер должны быть разными.
2) Получили CSP с переменными из множества {1, 2, 3} и клаузами размера 2. Делаем такие итерации: если есть какая-то плохая клауза, рандомно поменяем одну из переменных клаузы.
Далее, рассмотрим какое-либо корректное решение x0, и функцию F(x) = количество элементов в x, отличающихся от элементов x0. Если x — некорректное решение, то для невыполненной клаузы есть по крайней мере одна переменная, такая что если её изменить, то F(x) уменьшится. Получаем марковскую цепь на значениях F(x), и оценку вероятности на интересующие нас переходы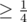 (т.к. есть 4 способа поменять переменную в клаузе). Если аккуратно посчитать, вроде получается оценка.
(т.к. есть 4 способа поменять переменную в клаузе). Если аккуратно посчитать, вроде получается оценка.
P.S. Почитал статью по ссылке внимательнее, там упоминается такой алгоритм как у нас, см. "U. Sch¨oning. A probabilistic algorithm for k-SAT and constraint satisfaction problems." И он даёт 1.5n, в то время как в статье по ссылке 1.3645n.
Такой вопрос по задаче G: раз уж с каких-то пор (я не понял насколько давно это началось) стали говорить, что в решении нет logn, т.к. оно юзает на set а hashset, то можно ли привести реализацию hashsetа которая работает совсем быстро (ну хотя бы в 10 раз быстрее setа). Потому, что HashSet в джаве сегодня работал очень медленно, а все что я писал руками не давало ускорения больше чем в 2-2.5 раза (а ускорение в 2 раза трудно назвать изменением асимптотики в рамках СП).
Ну а как об этом ещё говорить? Формально HashSet работает за O(1). При этом TreeSet мощнее, так как поддерживает сортировку. Фактически в олимпиадных задачах из Java TreeSet и Java HashSet бывают быстрее оба.
Обычно говорят, что асимптотика такая-то с использованием HashSet-а, если это не ясно из контекста. Ну не врать же, что в задаче нужен TreeSet, если он там не нужен.
Я конечно может ошибаюсь но O(1) по моему это амортизационная оценка основывающаяся на хорошести хеш-функции (на том что она достаточно рандомо кидает по блокам). Просто нам на контесте изрядно пришлось попихать эту задачу и в какой-то момент я подумал, что авторское решение совсем другое без всяких сетов. А так получается что авторское такое же только с хаками. И все же главное из того что я спрашивал где взять нахаченную реализацию хеш-сета?
Расскажу конкретно про задачу G.
Берем мое решение, описанное выше. Время в решении будем делить на 3 части: чтение данных, подсчет хэшей строк, использование хэш-таблицы. Для решений с хэш-таблицей, реализованной руками cpp java, получаем следующие данные:
Теперь сравним со стандартными реализациями. Поскольку чтение данных и подсчет хэшей не меняются, я буду приводить только время работы структуры данных.
C++ показывает следующие результаты: (mingw g++ 4.7.2)
Java показывает следующие результаты: (java 1.7.0_13)
Исходники можно посмотреть здесь. Код на java получен, как быстрый перевод c++ на java, поэтому немного странно выглядит. Время работы подсказывает, что или я не умею пользоваться сортировкой на java и hash_map-ом на c++, или они правда медленные. Если вы знаете, как сделать быстрее, буду рад комментариям =)
Я не знаю как ты это делаешь, но у меня вчера HashMap работал больше 7 секунд на Java. То же самое с mapом C++.
Спасибо за хорошую реализацию HashSetа.
Там по ссылке есть мой код =) Посмотри, расскажешь потом, в чем разница.
Похоже основная разница того, что пихали мы и того, что написал ты заключается в этом: мы перебирали строку, а потом все маски для нее, ты же делал наоборот сначала маску потом строку. Поэтому у тебя в кеш видимо получше попадало, и в hashmapе хранить надо было одно число, а не 2. Вывод я для себя сделал такой: стандартные hashsetы достаточно бестолковые, а ручные норм. Я всегда пишу hashsetы цепочками и поэтому они сильно медленнее того, что написал ты. Но для при открытой адресации мне не понятно как удалять из hashsetа?
Хреново удалять. Можно, но очень аккуратно
Удалять можно так: помечаем ячейку, откуда удаляем элемент, специальной пометкой "битая ячейка". Не "пустая ячейка", тогда все сломается, а именно "битая".
Добавление после этого нужно поменять так: если мы встретили битую ячейку, где лежит то, что мы добавляем, сказали, что теперь ячейка нормальная.
Ох, а я такую порнографию по этому поводу писал...
А как, перебирая все строки, а для каждой строки маски, получить O(n) памяти? может быть, у вас было O(2k n) памяти? Тогда понятно, почему медленно.
Да у нас было O(2kn) памяти
Ну конечно обычный HashSet горааздо тормознее, ведь в реализации Burunduk1 даже boxing/unboxing нет. В нормальных библиотеках для java есть нормальные HashSet'ы, но к сожалению в стандартную библиотеку они не включены.
По-моему, как раз HashMap на java офигенен. Почему так не знаю, но см. числа выше:
Написанный руками hash-table дает 0.453 seconds, стандартный HashMap дает 0.546 seconds. Всего на 20% хуже. Это же круто =)
Илья и люди, плюсующие Илью. Объясните, пожалуйста, откуда такой вывод "HashSet горааздо тормознее"? Не спорю, иногда он сильно медленней. Но конкретно в нашей задаче он почти также быстр, как и написанный руками (см. времена работы).
Руками можно написать гораздо эффективнее; например, если взять HashSet и руками переправить все "T" на "int" (ну или "long", в зависимости от того, что нужно в задаче). Т.к. HashSet мало того что памяти больше кушает, так ещё и делает unboxing при обращении к любому элементу (что плохо вдвойне: если есть массив int[] a, помещающийся в кэш, то все обращения к нему будут быстрыми; а в случае Integer[] каждый unboxing будет давать промах кеша).
Конечно, можно понадеяться, что JIT что-нибудь соптимизирует, но обычно получается, что он не помогает. По-хорошему, в Java нужны отдельные реализации HashSet для int, long, etc., однако в стандартной библиотеке их почему-то нет.
Сергей, а реализация открытой адресации последовательными пробами не приводит иногда к длинным кластерам? Вроде считается, что она этим плоха (а хороша, конечно, крутым попаданием в кэш).
Нет. А почему так должно получаться? Доказательство времени работы:
Пусть мы в хэш-таблицу размера n уже положили n-k чисел. Если функция хэширования хорошая, то у нас осталось k случайных пустых ячеек с номерами от 1 до n. Отсортируем их. Матожидание расстояния между соседними элементами в массиве k отсортированных чисел от 1 до n равно n/k. Получаем, что матожидание времени одного запроса к хэш-таблице равно 1 + n / 2k. То есть, если k не меньше n/2, то обращение к хэш-таблице сделает в среднем 2 просмотра. Итого: если хранить n элементов в таблице размера 1.5*n, то все ок.
UPD: извиняюсь за правки -- это я неудачно пробовал n / 2k поменять на \frac{n}{2k},
1. Матожидание расстояния между соседними элементами в массиве k отсортированных чисел от 1 до n равно n/k.
2. Получаем, что матожидание времени одного запроса к хэш-таблице равно 1 + n / 2k.
Мне кажется, этот переход неверен. Матожидание — это не вся информация, которая у нас есть. Представь себе, что в зацикленном массиве из n элементов первые n/2 заполнены, а вторые n/2 нет. Среднее расстояние между соседями (то есть матожидание этого расстояния) равно 2. Но при этом одно добавление в эту таблицу будет обрабатываться в среднем за n/8 шагов: в половине случаев за 1 шаг, в другой половине случаев за 2, 3, ..., n/2 (sum ~ (n/2)^2 / 2 = n/8) шагов.
Вот тако
Вот такой warning вываливается при использовании hash_map :-) In file included from c:\program files\mingw\bin../lib/gcc/mingw32/4.6.2/include/c++/backward/hash_map:61:0, from similar_sk_hash_map.cpp:14: c:\program files\mingw\bin../lib/gcc/mingw32/4.6.2/include/c++/backward/backward_warning.h:33:2: warning: #warning This file includes at least one deprecated or antiquated header which may be removed without further notice at a future date. Please use a non-deprecated interface with equivalent functionality instead. For a listing of replacement headers and interfaces, consult the file backward_wa rning.h. To disable this warning use -Wno-deprecated. [-Wcpp]
Мне тоже такой вываливается. Год назад еще не было такого... Видимо, с тех пор оно уже "deprecated or antiquated". Каким в таком случае предлагается пользоваться (без c++0x) -- не понятно.