Всем привет! Как-то я придумал такую функцию F(x):{2,3,...}->N: если x-простое, она равна его номеру в ряде простых чисел, если составное — то номеру в ряде составных чисел. Очевидно, что какое бы натуральное число мы не взяли, после нескольких применений этой функции получится 1. Например: F(22)=13, F(13)=6, F(6)=2, F(2)=1.
А теперь давайте построим такое бесконечное бинарное дерево: в корне стоит число 1, для каждой вершины, в которой записано число N левый сын — это N-тое простое число, правый сын — N-тое составное число. Получится примерно следующее: 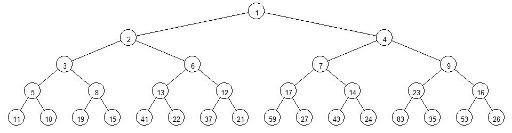 Это дерево обладает следующими свойствами:
Это дерево обладает следующими свойствами:
- В нём содержатся все натуральные числа;
- Родитель вершины с числом N — это F(N);
- Для любой вершины путь от неё до корня — это последовательность чисел, получаемых при многократном вычислении функции F(x).
Не знаю, может ли оно иметь какое-то применение, но мне кажется, что оно не лишено некоторой красоты. Кроме, того, подобное дерево можно построить по любым двум непересекающимся множествам, которые в объединении дают множество натуральных чисел кроме единицы (если же в одном из множеств будет число 1, то почти ничего не изменится, просто появится петля из корня в себя, но это уже будет не дерево).











А можете объяснить почему в таком дереве будут содержаться все натуральные числа?
UPD. Понял сам.
Функция F(N) возвращает число строго меньше N, но больше 1. Значит, для любого натурального N многократное выполнение этой функции даёт 1. Но каждой цепочке N -> F(N) -> F(F(N)) и т.д. в дереве отвечает путь. А так как этот путь содержит 1, и вершина 1 есть в дереве, значит, и вершина N есть в дереве.
Если в одном множестве есть 1 и 2 , то петля может быть и не только из 1 в 1, но и из 2 в 2:)
Ну и видимо нам хочется бесконечные множества, иначе получится какой-то изврат.
Oh man, why on earth would you use two negatives (..not without..) and hinder me understanding things XD.
Soo, I got to use my algorithm to change that sentence into a one I can understand.
So, removing both of negatives from there. Hm...
"...but it seems to me that it is with a certain beauty.." !!!!
I am awesome : D
OK. to the point, you too are awesome xD