Hello everyone!

This time I’d like to tell you about a data structure from 1983 which, I believe, deserves to be widely known in CP community. This structure solves the problem of quickly finding ancestors in a rooted tree. Like usual binary lifting, it does so in $$$O(\log n)$$$. But unlike with usual binary lifting, you can add and remove leaves in $$$O(1)$$$, which means that the total space requirement is just $$$O(n)$$$.

Each node in the tree requires the following fields:

class Node {
  int depth;
  Node parent;
  Node jump;
}

Here depth is the number of times you need to .parent the node in order to reach the root. Field jump points to some ancestor of the node.

Below is the definition of the root node. Its jump pointer is undefined, but it turns out convenient if it points to the root itself.

root.parent = null;
root.depth = 0;
root.jump = root;

Here’s how you find an ancestor that has specified (smaller) depth:

Node find(Node u, int d) {
  while (u.depth > d) {
    if (u.jump.depth < d) {
      u = u.parent;
    } else {
      u = u.jump;
    }
  }

  return u;
}

The implementation is straightforward because there’s not much you can do with a pair of pointers. We simply go up towards the target node, occasionally taking a jump whenever we are sure that it won’t skip the target.

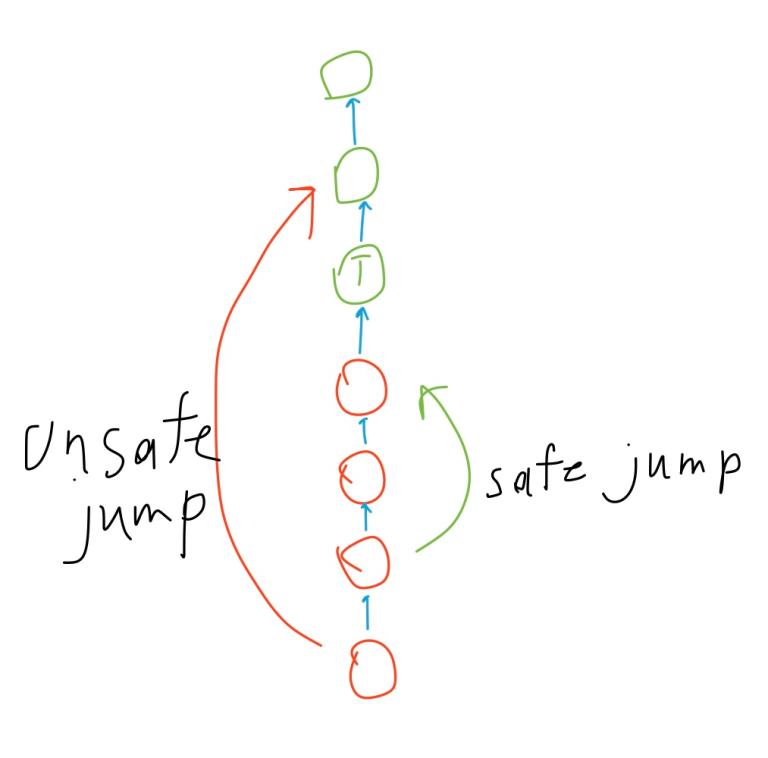
Jump pointers

Now let’s define the jump pointers. Here’s how you create a new leaf:

Node makeLeaf(Node p) {
  Node leaf = new Node();
  leaf.parent = p;
  leaf.depth = p.depth + 1;

  if (p.depth - p.jump.depth == p.jump.depth - p.jump.jump.depth) {
    leaf.jump = p.jump.jump;
  } else {
    leaf.jump = p;
  }

  return leaf;
}

Parent and depth assignments are hopefully obvious. But what is this?

p.depth - p.jump.depth == p.jump.depth - p.jump.jump.depth

Unfortunately, proper rigorous explanation is quite intimidating. If you want to read it, I direct you to the original 1983 paper of Myers called “An applicative random-access stack”.

If you don’t feel like reading about properties of canonical skew-binary representations, I’ve got some drawings that hopefully will give you rough ideas and intuitions and, most importantly, the confidence required to code and use the structure properly under the pressure of real competition.

Below is an illustration of the case when the equality holds:

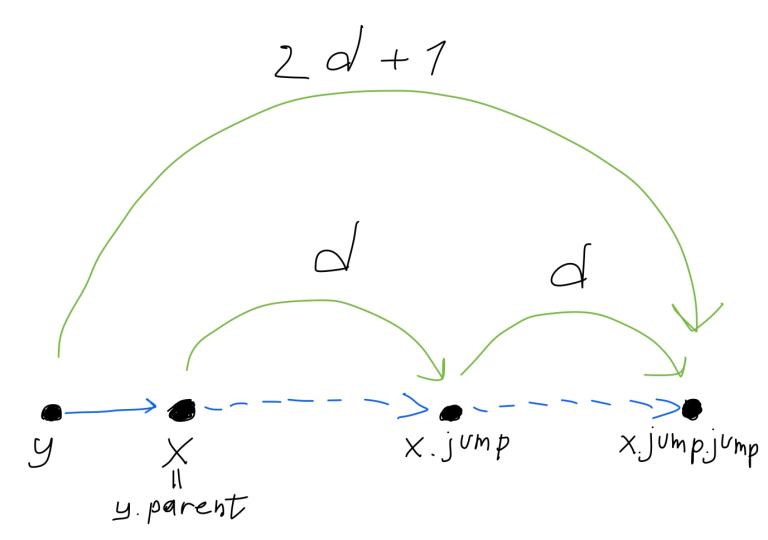
Here y is our new leaf. Blue arrows are paths formed by parent links, green arrows are jumps. Each green arrow has a length of the jump written above it. Important thing to notice is that our find algorithm will first try a $$$2d+1$$$ jump, and if it happens to be too long, it will go to the parent. This parent has a smaller jump, at least twice shorter.

This is almost what a conventional binary lifting would do. But instead of cramming all the jumps of different lengths into single node, it spreads them amongst the ancestors.

Okay, this explains how it exponentially reduces the size of a jump. But what if our very deep node happens to have only a very short jump? How reducing such a jump might help? To answer that, let’s look at bigger picture:

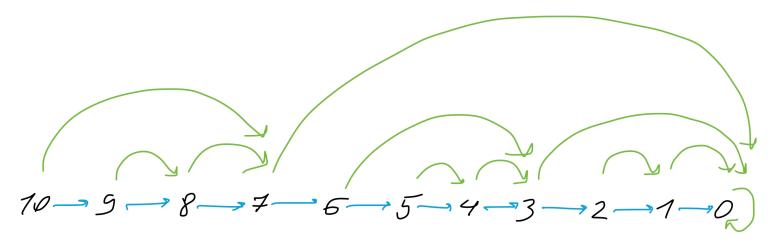
This picture is not really that big, but I hope it helps you to grasp the whole scheme. Notice that no farther than two jumps away there’s always a 2x or longer jump, if such a jump is possible at all. That is, if you keep jumping, the size of the jumps grows exponentially. This roughly explains how find manages to work in logarithmic time:

1. It gains speed exponentially by encountering larger and larger jumps.
2. It slows down by looking at parent’s shorter jumps.

At this point it is clear that actual number of steps done by find is not just a binary logarithm. Indeed, the original paper gives the following upper bound, where $$$d$$$ is the depth of the starting node:

I didn’t perform any tests, but this might be practically three times slower than conventional binary lifting.

Binary search on the ancestry path

You might be tempted to implement standard binary search and use find as its subroutine. This would be $$$O(\log^2 n)$$$. Luckily, we can repurpose find instead.

Node search(Node u, Predicate<Node> p) {
  while (!p.test(u)) {
    if (p.test(u.jump)) {
      u = u.parent;
    } else {
      u = u.jump;
    }
  }

  return u;
}

This function returns the deepest ancestor for which the predicate holds. This particular implementation assumes that such an ancestor always exists. Basically, we approach the target step by step, occasionally jumping, if we’re sure that we wouldn’t skip the target.

Finding LCA

Here LCA finding relies on two things:

1. If the two nodes have different depths, we can quickly equalize them using find.
2. The jump structure depends on nothing but depth.

The last point means that we can do a search simultaneously on both nodes — they’ll be at the same depth throughout the process. Then we can find LCA using the approach of binary search. We simply check whether the two nodes coincide to detect if we are past the LCA:

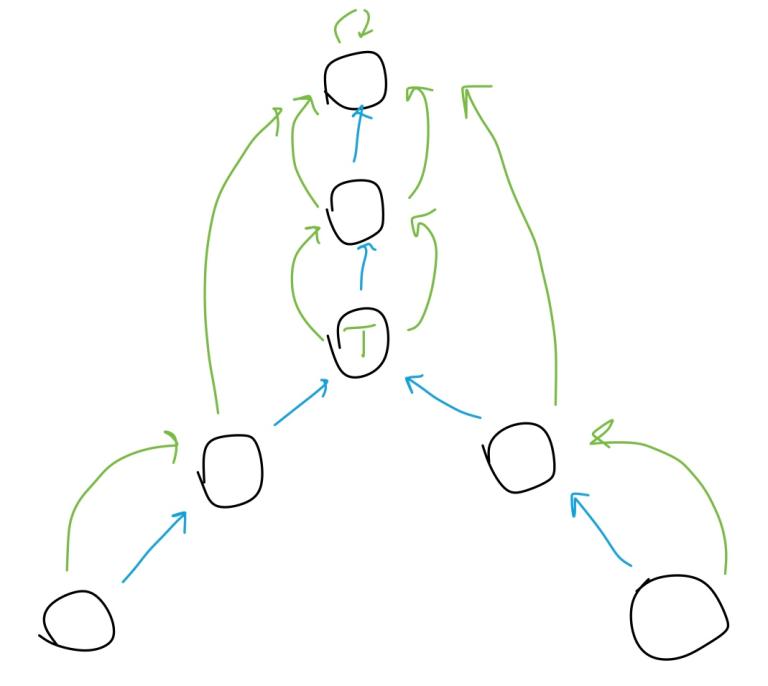
Node lca(Node u, Node v) {
  if (u.depth > v.depth) {
    return lca(v, u);
  }

  v = find(v, u.depth);

  while (u != v) {
    if (u.jump == v.jump) {
      u = u.parent;
      v = v.parent;
    } else {
      u = u.jump;
      v = v.jump;
    }
  }

  return u;
}