300A - Массив
В этой задаче нужно было просто реализовать следующий алгоритм. Разделим входной массив на 3 вектора: первый будет содержать все отрицательные числа, второй — все положительные числа, третий — ноль. Если первый вектор содержит четное количество элементов, то переместим ровно одно число в третий вектор. Если второй вектор пуст, то переместим ровно 2 элемента из первого вектора во второй.Такое решение работает за O(n)
300B - Тренер
Заметим, что входных данных задан некоторый граф. Заметим, что если в этом графе есть хотя бы одна компонента связности, в которой как минимум 4 вершины, то ответ очевидно - 1. Сразу следует заметить, что все компоненты связности, в которых уже ровно 3 вершины, уже образуют некоторую команду. Далее у нас остались компоненты связности, в которых либо 1 вершина, либо 2. Не трудно понять, что если количество компонент, в которых ровно 2 вершины больше количества компонент с 1 вершиной, то ответ - 1. Иначе решение существует. Каждой компоненте из 2 вершин сопоставим одну компоненту из 1 вершины. Далее соединим все одноэлементые компоненты в группы по 3. Таким образом, получим решение за ассимптотику O(n + m).Также следует отметить, что также можно было написать решение и за ассимптотику O(n4).
300C - Прекрасные числа
Пусть MOD = 1000000007. Для начала подсчитаем массив fact[i] = i!%MOD, 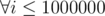 . Далее будем перебирать, сколько раз встретится цифра a в искомом числе. Пусть она встречается i раз. Тогда очевидно, что мы можем подсчитать какова сумма цифр в нашем числе сейчас: val = ai + b(n - i). Если число val — хорошее, то к ответу нужно прибавить C[n][i]. Однако n слишком большее, чтобы считать биномиальные коэффициенты используя треугольник Паскаля. Тогда C[n][i] = fact[n]inv(fact[n - i]fact[i]). inv(a) — обратный элемент в кольце по модулю. Так как модуль простой, то inv(a) = aMOD - 2. Возвести число a в степень, можно используя бинарное возведение в степень.
. Далее будем перебирать, сколько раз встретится цифра a в искомом числе. Пусть она встречается i раз. Тогда очевидно, что мы можем подсчитать какова сумма цифр в нашем числе сейчас: val = ai + b(n - i). Если число val — хорошее, то к ответу нужно прибавить C[n][i]. Однако n слишком большее, чтобы считать биномиальные коэффициенты используя треугольник Паскаля. Тогда C[n][i] = fact[n]inv(fact[n - i]fact[i]). inv(a) — обратный элемент в кольце по модулю. Так как модуль простой, то inv(a) = aMOD - 2. Возвести число a в степень, можно используя бинарное возведение в степень.
300D - Покраска квадрата
Эта картинка полезна для понимания.

Переформулируем задачу в терминах графов:
Нам задана таблица n × n, которая представляет некоторый граф следующего вида:
- Этот граф — дерево
- У всех вершин, кроме листьев, ровно четыре сына
- Пусть некоторая вершина удалена от корня на расстояние k. Тогда существует ровно 4k вершин, которые также удалены на расстояние k.
Нам нужно покрасить ровно k вершин этого графа. Причем, если вершина i покрашена, то тогда покрашены все вершины, лежащие на пути из вершины 1 до вершины i.
Понятно, что мы можем однозначно восстановить дерево по его высоте. Высоту графа можно найти с помощью простого кода:
int height = 0;
while (n > 1 && n % 2 == 1) {
n /= 2; height++;
}
Поэтому заведем следующее динамическое программирование: z[i][j] — количество способов раскрасить граф высоты i за j операций.
Можно привести простой код решения за ассимптотику O(k4log(n)):
z[0][0] = 1; z[0][i] = 0, i > 0; z[i][0] = 1, i > 0
z[i][j] = 0;
for(int k1 = 0; k1 <= j - 1; k1++)
for(int k2 = 0; k2 <= j - 1 - k1; k2++)
for(int k3 = 0; k3 <= j - 1 - k1 - k2; k3++)
{
int k4 = j - 1 - k1 - k2 - k3;
z[i][j] += z[i-1][k1] * z[i-1][k2] * z[i-1][k3] * z[i-1][k4];
z[i][j] %= mod;
}
Однако такое решение работает долго. Пусть z[i][j] — означает что оно и означало раньше:количество способов раскрасить граф высоты i за j операций. Однако посмотрим на него с другой стороны: z[i][j] — коэффициент при j степени i-ого многочлена. Тогда не трудно заметить что z[i + 1][j + 1] — коэффициент при j степени i-ого многочлена, возведенного в 4 степень. Таким образом получим решение за ассимптотику O(k2log(n)). Модуль, указанный в условии, позволяет так же воспользоваться быстрым преобразованием Фурье и написать решение за ассимптотику O(klog(k)log(n)). Однако такое решение все равно может получить ТЛ, если вы часто будете брать по модулю. Так как модуль довольно не большой ( ≤ 107) можно брать по модулю реже. Это позволяет ускорить работу решения в несколько раз.
Авторское решение. Использует FFT
300E - Империя наносит ответный удар
Пусть 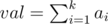 . val это верхняя граница ответа. val! делится на
. val это верхняя граница ответа. val! делится на 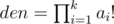 , это просто доказать, используя то факт, что
, это просто доказать, используя то факт, что 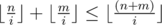 . Так же,
. Так же, 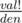 — мультиномиальный коэффициент. Итак, ответ не превосходит 1013.
— мультиномиальный коэффициент. Итак, ответ не превосходит 1013.
Если n! делится на den, тогда (n + 1)! также делится на den. Это означает, что мы можем использовать бинарный поиск по ответу.
Для всех i, i = 2..., 107, посчитаем максимальное простое в i, используя линейное решето Эратосфена. Пусть для i — это lp[i]. Также предпосчитаем все простые ≤ 107.
Далее предпосчитаем cnt[i] — количество чисел a, i < = a.
Теперь мы можем посчитать факторизацию знаменателя:
for(int i = max; i>=2; i--) {
if (lp[i] != i)
cnt[lp[i]] += cnt[i];
cnt[i / lp[i]] += cnt[i];
}
Далее воспользуемся бинарным поиском от lf = 1 до 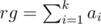 .
.











А что делать тем, кто не знает FFT? Как-то не подходит Д-шка для див-2.
Так за квадрат же перемножать можно, k маленькое.
Так ведь k^2 = 10^6 и при этом 10^5 запросов. Явно ТЛ :)
Просто оставлю здесь это: 3626252
Окай, я дурак :(
Конкретно в этой задаче вроде бы норм проходит и тупое умножение. Если не грешить лишними %mod.
Но в целом... Это, кстати, типичная практика div2 only контестов. Если в обычных матчах div2 D,E — это что-то более-менее креативное и не слишком реализационное, потому как те же задачи идут в div1 B,C, и там различная ересь просто идейно не вписывается, то в div2 only контестах авторы часто грешат тем, чтобы дать задачу, которая будет, возможно даже, не слишком уж идейной, но будет требовать использование какого-нибудь бора, суф.автомата, не совсем примитивного дерева отрезков, FFT или еще чего-нибудь в этом роде.
Не знаю, хорошо это или плохо, но как-то не в моем вкусе) Хотя, мне-то что, я в div2 в ближайшее время не собираюсь)
Но сегодня вроде бы все решаемо без этого скучного "напишите здесь FFT", так что от меня плюсик авторам, которые со своим первым контестом справились очень даже неплохо)
Можно проще: посчитаем 3 динамики — d1[k][depth], d2[k][depth] и d4[k][depth].
d1 — сколько способов раскрасить, если у нас есть k действий, максимальная глубина depth и 1 квадрат. d4 — тоже самое, но у нас есть 4 квадрата, d2 — есть 2 квадрата.
Каждая из динамик пересчитывается через другие за O(k) => получаем k2logN.
http://codeforces.net/contest/300/submission/3627397
Можно избавиться или от d1 или от d4. Я тоже писал это решение, однако, пришлось его "пропихивать". У меня оно работало over 10s. Так как я пишу на Дельфи, то я просто отправил под free pascal, и у меня зашло. free pascal довольно быстро работает с int64 и взятием по модулю. P.s. В решении можно совершить в 2 раза меньше операций, если вместо действий "прибавить d[depth][j]*d[depth][i — j] и прибавить d[depth][i — j]*d[depth[j]", бежать до половины цикла, просто домножая значения на 2.
А почему в задаче С надо добавлять к ответу C[N][I]? Я взял количество возможных перестановок, то есть n! / (i! * (n — i)!), но это оказалось неверным.
Должно быть, вы ошиблись в реализации.
Я вот искал inv(a) при помощи алгоритма Евклида и получил TLE :(
UPD: Не, Евклид таки не виноват, я сам дурак :)
Сомневаюсь я, что эти строчки
сокращают правильно.
Это уже в порядке бреда. Стал эксперементировать. 3626434 Что насчет этого решения?
У вас на каждом шагу переменная
ansберется по модулю, при этом вы пытаетесь проверить ее делимость на другое число. Думаю, это работает некорректно.Мда, видимо так, спасибо
Я понять не могу, почему эта ветка уходит в минусы?
А можно поподробнее этот момент?
И не проще ли считать С через факториалы по модулю?
нам нужно посчитать n!/a mod m. n!/a mod m = n! * a^-1 mod m, где a^-1 такой элемент, что a*a^-1 = 1 (mod m). по теореме Эйлера, a^phi(m) = 1 (mod m), где phi(m) = функция Эйлера. Т.к. m — простое => phi(m)=m-1; a^(m-1) = 1(mod m); a^(m-2) * a = 1 (mod m) => a^(m-2) = a^-1 .
What is O(n^4) solution for B?
I used Floyd-Warshall which works in O(n^3).
По задаче С. Я прочитал, как рекомендуют находить считать биномиальные коэффициенты, но я не понимаю, почему по формуле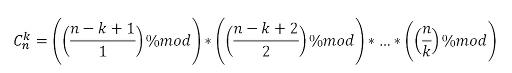 считает НЕ правильно. Понятно, если долго, но почему не правильно?
считает НЕ правильно. Понятно, если долго, но почему не правильно?
n — k + 2 может оказаться нечетным и при делении теряется 0.5, также при других случаях.
ой. что-то я протупил. не так записал формулу(( вообще я считал так
c=1; long long k1=1;
for (long long j=n-k+1; j<= n; j++, k1++) { c*= j; c/= k1; c%= MOD; }
тут я делю с, а оно точно кратно нужному числу
Прочитайте :D
спасибо
Authors solution for E looks to be a different program from the intended.
thanks. Now fixed.
"Однако посмотрим на него с другой стороны: z[i][j] — коэффициент при j степени i-ого многочлена. Тогда не трудно заметить что z[i + 1][j + 1] — коэффициент при j степени i-ого многочлена, возведенного в 4 степень."
Можно поподробнее, а то мне, если честно, трудно заметить :)
Изначально про многочлен не думали (ну я по крайней мере), было решение за 4 степень. Пусть действительно у нас есть такой переход с многочленами, предположим. Тогда в решении за 4 степень что делается — перебирается степень j элемента текущего многочлена, потом перебираются все 4-ки (k1, k2, k3, k4), c учётом порядка, которые в сумме дают j. Коэффициенты при k1, k2, k3, k4 перемножаются и прибавляются к текущему при j, что эквивалентно возведению многочлена в 4 степень. Надеюсь стало понятнее :)
I think by mistake both are same link in D
Thank you.
Really great to have the analysis so quickly, btw!
About solution C, I will appreciate a theory reference for the MOD-2 theorem in the inverse! Thanks
You can read it here, for example. It's based on Euler's theorem.
For solution D, can you (or someone) explain what are the following pieces of code doing?
It's basically splitting power of 4 into two square operations. The first calculates power of 2 on the polynomial, stored into a temporary array, then the second calculated power of 2 on the temporary array.
Thanks! but I don't really understand this too:
Let's consider current DP as polynomial coefficients: z[i][j] — coefficient of power j of polynomial i. In that case z[i + 1][j + 1] — coefficient of power j of polynomial i to the 4-th power.
what does that mean by "to the 4-th power" and why is that the answer?
Is it just me or is E actually easier than D? (I used an approach different to the max-prime, instead I used a modified sieve of Erathostenes to determine the exponent of each prime in the product by looping through all the integers divisible by it and getting max. powers of this prime dividing each of them.) Almost did it during the contest, too... or maybe I just like number theory :D
can anybody clarify the naive solution of D ? I cant understand it although read again and again..
firstly,we can calc how many times can we divid the square,if two square have the same times of divding,their answers is the same,so we just care about how many times the square can be divided. secondly,we can find the**_ subproblem_** of this problem , if we divide a square into four parts,and we can assigned every part a number(dividing times)__ , for example :a b c d. it means part1 be divided a times , part2 be divided b times ..and so on. we'd better construct the square from small to big. So the dp state is dp[i][j] :the tot number of ways when we are constructing the ith small square , we have draw j times , every step ,the square just become two times bigger. the transion is simple , just enumerate the four parts's draw times respectively , and we got a two size bigger square,when doing transion ,we must use a little optimizatioin see my code here
thanks a lot! you write clearly i understand now :)
Man, you are the real MVP
for Problem E,I've seen this code ,but I can't understand what does the following code try to do
anyone help me ? thanks a lot
Delta[i] is the number of times that i is being multiplied in the denominator, that is, the number of x's such that a[x] >= i. It is calculated in such a way that if you get the sum of Delta[i] * i for all i, that sum would be the denominator.
Min[i] is the index of the minimum prime number that divides i.
Count[i] is the number of times that the denominator can be divided by the ith prime. So what he does in that for is really factoring the denominator in prime factors in an efficient way. Another way of doing it is: for each i, for each prime factor x of i, count[indexOfPrime[x]] += Delta[i] * timesDivide(i, x). But this way is less efficient.
An example: suppose i is the the number (2^3) * (3^4) = 648 and that 648 is 5 times in the denominator (for example if the denominator is 1000! * 648! * 649! * 700! * 701!), then you would add to count[indexOfPrime[2]] the value 5 * 3 and to count[indexOfPrime[3]] the value 5 * 4.
At the end the denominator is factored in this way denominator = 2 ^count[0] + 3 ^ count[1] + 5 ^ count[2] + 7 ^ count[3] + ... + i ^ count[indexOfPrime[i]] and you can continue with the binary search.
As a guy with limited programming experience and weak maths, the tutorial for E was a little over the head for me.. Can someone please explain the solution in a better way with each step elaborated properly..??? thanks in advance..
It's hard for me to explain ,but anyway , I will try. First'y we should get lp[i] as the editorial says. and then we should use lp[i] to split all the numbers
cnt[i] is the times prime factor i appear , initially cnt[i] is the numbers bigger than i , so cnt[lp[i]] += cnt[i] and cnt[lp[lp[i]]] += cnt[i].. and so on. but the way of the code above is faster and clever .
How to proof the problem C's solution: "MOD is a prime number, so inv(a) = a^(MOD - 2)"?
Fermat's little theorem. We know that a^(MOD-1)=1 modulo MOD. By definition, inv(a)=a^(-1) and multiplying by a^(MOD-2) gives inv(a)=a^(MOD-2). (The equalities are in fact congruences.)
Note that this is only valid for coprime a and MOD.
Have a look at this article too...
http://en.wikipedia.org/wiki/Euler's_theorem
the fermat's theorem is a case of euler's theorem, with the totient function being equal to (p-1), where p is prime.. i hope it satisfies u...
Thank you very much!
Ввод 5 -1 -2 1 2 0 Вывод 1 -2 2 1 2 1 0 -1 Ответ 1 -1 2 1 2 2 0 -2 Подскажите в чем ошибка. Ответ удовлетворяет описанные условия.
In the author's solution of problem D what is the significance of the value of root_1?
I know it's very late but I would really appreciate if someone could help me with understanding this statement regarding problem D-
"Let's consider current DP as polynomial coefficients: z[i][j] — coefficient of power j of polynomial i. In that case z[i + 1][j + 1] — coefficient of power j of polynomial i to the 4-th power. "
What is the meaning of 'coefficient of power j of polynomial i'? What does one mean by 'polynomial i'?
gridnevvvit can u please share the image related to problem D or explain what is there in the image as I am not able to view it? I also tried going to the url of the image but had no success. Thanks in advance.
Also in problem D, how do you model n * n matrix as a graph (tree) with each node having 4 children? What is the root of the tree?
Why permutations with repetitions doesn't solve problem C?
you can solve with permutations, but its a different type of permutation, see this link
I used DSU to solve problem B with $$$O(n^2log(n))$$$. Mine
Hello Everyone!!
I was solving the C problem of this contest and getting "Time Limit Exceeded". I don't know where to optimize further. I also looked at the author's solution and I guess it is pretty much the same. It would be great if someone could walk me out of this problem.
The link to my solution is: 74799789
TIA
Ignore this comment. I found my mistake :)
No. I've checked all the TCs now and they are all <=1e6. Can you tell which TC exactly crosses this limit?
O(N) solution for problem C 98275817
I don't know how to solve Problem A, it's not logic for me
In the first line print integer n1 (n1 > 0) n1 output have minus number In the next line print integer n2 (n2 > 0) n2 output have minus number In the next line print integer n3 (n3 > 0) n3 output have minus number
I think, this question is wrong ? I don't know
and n1 n2 n3 cannot empty it should be a close number but the output isn't