oversolver's blog

Most useless property of tree?
By oversolver, 5 years ago, In English

Given a rooted tree.

Suppose query (v,d) is set of vertices in subtree of v in depth d from v.

Let's take all possible queries and leave only distinct sets.

Sum of sizes of these sets is $$$O(n\sqrt{n})$$$.

Actually, idk how to prove it. If you know proof, please post it here.

I met it in one Gerald's lecture with proof like "try to construct worst case and you see it".

I can construct such family of trees with $$$f(k)\approx \frac{n \sqrt n}{2}$$$ where $$$n(k) = \frac{k(k+1)}{2}$$$

Here tree with k=4: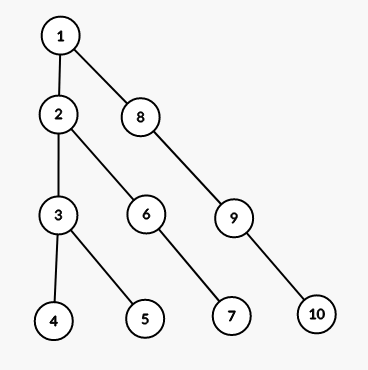

Only two times I tried to apply this as base of my solutions. But it was 1) useless — there are was easiest ones 2) painfull.

If you have some problems for this feature, post it please.

  • Vote: I like it
  • +52
  • Vote: I do not like it

»
5 years ago, # |
← Rev. 7   Vote: I like it +6 Vote: I do not like it

Wrong

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    Consider tree as [bamboo] + [star in bottom]:

    edges (1,2), (2,3), ... ,(n/2-1,n/2) and (n/2,n/2+1), (n/2,n/2+2), ..., (n/2,n)

    lowest array in height n/2 has size more than $$$\sqrt{n}$$$

    → Reply
»
5 years ago, # |
  Vote: I like it +34 Vote: I do not like it

Maybe smth like this. Lets calculate for every vertex $$$v$$$ number of distinct sets containing it. Assume we are checking set $$$(p, d)$$$. If we want to count $$$v$$$, set $$$(p, d)$$$ must differs from set $$$($$$ancestor of $$$v$$$ on dist $$$d - 1, d - 1)$$$. So there at least should exists path of length $$$d$$$ starting in $$$p$$$ such that it`s second vertex is not ancestor of $$$v$$$. So every vertex can lie only in $$$\mathcal{O}(\sqrt n)$$$ such sets.

→ Reply