ACM ICPC World Finals Warmup is scheduled to take place at UVa Online Judge on Saturday, 25th May 2013.
Contest Link: ACM ICPC World Finals Warmup
Date: 25th May, 2013
Day: Saturday
Start: 9:00 AM, GMT
Duration: 5 hours
If you are getting a redirect loop when trying to access the link, remove the cookie onlinejudge.org and try again.











Reminder: The contest starts in under 12 hours.
how to solve problem C (Rectangle XOR Game) ?
The problem J is still broken.
I have sent a detailed e-mail to Miguel Revilla.
When it will be fixed?
Yep. The fact is that the 10^9 upper bound mentioned in the problem statement does not apply to the test cases. Instead, a larger upper bound of about 3*10^9 should be considered in order to solve the problem (so that (3*10^9)^2 still fits into a long long). I'm sure this mistake caused a lot of contestants to keep getting WA with an otherwise perfectly correct solution (I spent more than 2 hours during the contest trying to debug my actually correct solution ; only several hours later, when I tried to find which cases made my solution fail, I found the problem with the test cases).
How to solve problem J? Any particular hint?
They have already fixed the bug with upper bound and rejudged all submissions.
But now they allow equal numbers in the solution
and without this you can't find the solution in some situations.
So after rejudge a lot of contestants lost their AC (including me an you).
That's weird, because I have a check in my program that ignore all solutions that have equal numbers, and I still got accepted :D
Oh, I see. I haven't checked for rejudges. I now see that I lost the AC from the contest. I resubmitted my code in the problem archive without the explicit check that the numbers should be different and I got AC. Anyway, it seems that they just can't get this problem right :)
We are aware of the issue. There should be another rejudge after the correction. Sorry about all these!
Any suggestions on problem E? I've solved its first part with "dp[A] — number of subsets which gcd is A", but can't apply this dp to case of K-subsets faster then O(nk). I think such kind of problems "2 in 1" are not good cause it doesn't distinguish participants who spent on this problem several hours and solved one of subtask and participants who haven't ever read the statement. Thanks
Both sub-problems can be solved by inclusion-exclusion principle.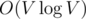 , where V = 100000 is an upper bound for numbers, by some kind of sieve.
, where V = 100000 is an upper bound for numbers, by some kind of sieve.
Let cnt[d] be the number of elements divisible by d.
It can be found in
Then answer for the second sub-problem is
where
is the number of subsets with size $k$ and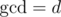 .
.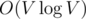 as well after precomputing Moebius mu function, powers of two and binomial coefficients (for example, by computing factorials and their inverses).
as well after precomputing Moebius mu function, powers of two and binomial coefficients (for example, by computing factorials and their inverses).
For the first sub-problem binomial coefficient should be replaced by 2cnt[dx] - 1.
The complexity for finding such double sum is