Задача A. Утренний бег

В задаче требовалось найти математическое ожидание количества встреч между бегунами. Как это делать? Для начала, вспомним, что математическое ожидание линейно, поэтому исходная задача эквивалентна следующей: найти сумму математического ожидания количества встреч между каждой парой бегунов. Будем решать задачу именно в этой формулировке. Сделаем несколько наблюдений:

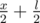1. Пусть расстояние между двумя фиксированными бегунами ровно x и они бегут навстречу друг другу бесконечно (вероятность того, что они бегут навстречу, как нетрудно видеть, равняется 0.5·0.5 = 0.25). Тогда первая встреча произойдет в момент времени , следующая — , следующая — 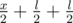и так далее.

2. Пусть каждый из бегунов бежал ровно l единиц времени. Тогда, если два бегуна встречаются, то они встречаются ровно 2 раза. Вероятность того, что два бегуна встретятся составляет 0.5, так как в двух случаях из четырех они бегут навстречу друг другу, а в оставшихся двух случаях бегут в одном направлении.

На основании этих наблюдений будем строить решение. Для начала разобьем t как t = k·l + p, где 0 ≤ p < l. Тогда, каждый из бегунов пробежит ровно k полных кругов. Что это означает? Так как всего пар бегунов ровно 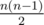, то за k кругов в каждой из пар с вероятностью 0.5 произойдет ровно 2k встреч. Значит, к ответу нужно добавить .

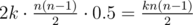Теперь как-то нужно обработать оставшиеся p секунд бега. Предположим, что расстояние между двумя бегунами ровно x и они бегут это расстояние навстречу друг другу. Тогда, между ними произойдет встреча, если 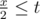, или x ≤ 2t. Между ними произойдет вторая встреча, если 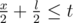, или x ≤ 2t - l. Больше двух встреч произойти не может, так как p < l.

Зафиксируем какого-нибудь бегуна, тогда с помощью двоичного поиска мы можем найти количество бегунов, которые находятся на расстоянии не более x от данного. Выберем границу x как x = 2t, и тогда количество бегунов на расстоянии не более x будет означать количество бегунов, которые встретятся с зафиксированным. Если же мы выберем x = 2t - l, то сможем найти количество бегунов, с которыми произойдет вторая встреча. Умножаем полученные количества на 0.25 — вероятность встречи бегунов, и добавляем к ответу.

Сложность такого решения составляет 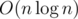. Ее можно улучшить, если вместо двоичного поиска использовать метод двух указателей.

Задача B. Контекстная реклама

В задаче требовалось найти максимальное количество слов, которое можно разместить в блоке размера r × c. Решим сначала следующую задачу: какое максимальное количество подряд идущих слов поместится в строке длины c, если первое слово имеет индекс i. Такую задачу можно решать двоичным поиском, или двигая указатель. Теперь создадим граф, где вершинами будут слова, а ориентированные ребра будут соединять вершины i и j, если слова с i по j - 1 помещаются в одну строку длины c, а слова с i по j уже не помещаются. Весом ребра будет величина j - i. Тогда исходную задачу можно переформулировать в терминах данного графа: требуется найти путь длины k, который имеет наибольший вес. Такую задачу можно решать со сложностью 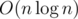используя метод двоичного подъема, или за O(n) при помощи поиска в глубину.

Сложности реализации были в том, что нужно было выводить не искомое максимальное количество слов, а полный текст, а так же в том, что требовалось работать со строками, а не с числами.

Задача C. Память для массивов

Здесь нужно было найти максимальное количество массивов, которое можно разместить в имеющейся памяти. Для начала отметим следующее: пусть ответ на задачу — это число k, тогда одним из оптимальных решений будет размещение k самых маленьких по размеру массивов в памяти. Без ограничения общности, будем считать, что у нас есть массивы размера 1 и мы хотим их разместить, при этом, разместить их как можно больше. Тогда, если у нас есть участки памяти нечетного размера, то при размещении массива размера 1 на таком участке, мы получим участок памяти четного размера. С другой стороны, если размещать на участке массивы другого размера, то четность не поменяется, и если на участке не будет размещено ни одного массива размера 1, то в самом конце в нем будет хотя бы одна свободная ячейка. Значит, выгодно размещать массивы размера 1 на участках памяти нечетного размера. Сделаем это, пока можем. Возможны три ситуации:

1. У нас закончились участки памяти нечетного размера.

2. У нас закончились массивы размера 1.

3. У нас закончились и участки памяти нечетного размера и массивы размера 1.

Начнем с первого случая. Пусть у нас остались массивы размера 1, но не осталось участков памяти нечетного размера. В оптимальном решении выгодно продолжать размещать массивы размера 1. При этом, если мы разместим их в участках памяти четного размера, то мы поменяем четность размера участка памяти, а как написано выше, это может привести к тому, что в конце процесса хотя бы одна свободная ячейка на участке памяти. Из этого можно сделать вывод, что невыгодно размещать массивы размера 1 по одному на участок. Выгодно объединить их в массивы размера 2 и размещать вместе. Сделаем это. После этого, разделим все имеющиеся числа на 2 и придем к изначальной задаче.

Во втором случае, если мы сразу разделим все имеющиеся числа целочисленно на 2, и решим изначальную задачу, то ответ мы не ухудшим.

Третий случай аналогичен второму.

Следует отметить, что после сведения задачи к аналогичной, нам требуется помнить, что всегда выгоднее размещать те массивы, которые были собраны из наибольшего количества массивов.

Сложность данного решения составляет .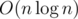

Задача D. Теннисные ракетки

Участникам требовалось найти количество тупоугольных треугольников на данных вершинах, удовлетворяющих некоторым условиям. Сразу отметим, что авторское решение имеет сложность O(n²), но имеет ряд оптимизаций, благодаря чему решение укладывается в TL с большим запасом.

Каждый тупоугольный треугольник имеет ровно один тупой угол. В силу симметрии задачи без ограничения общности мы можем зафиксировать сторону и считать, что тупой угол прилегает к этой стороне. Тогда, нам нужно посчитать ответ лишь для одной стороны, а в конце умножить его на 3.

Так как каждая сторона симметрична, то можем рассматривать лишь половину стороны, а после этого умножить ответ на 2.

Введем координаты, так что вершина A треугольника имеет координаты (0,0). Вершина B (0,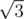) и C(2,0). Тогда найдем координаты каждой из точек на сторонах и выпишем теорему косинусов. Получим некое соотношение, которое гарантирует нам, что треугольник будет тупоугольным. Один из возможных его видов таков: Если 1 ≤ i, j, k ≤ n — номера точек зафиксированных на сторонах, то треугольник тупоугольный тогда и только тогда, когда: f(i, j, k) = 2i² - i(n + 1) + 2j(n + 1) - ij - k(i + j) < 0. Заметим, что 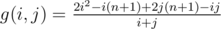возрастает, поэтому можем использовать метод двигающегося указателя для перебора k. Тогда просто переберем i от m + 1 до 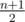, затем j от m + 1 до тех пор, пока верхняя граница для k не превосходит n - m + 1 и будем суммировать результаты.

Отметим, что все результаты нужно делать в типе int, что существенно ускоряет решение.

Задача E. Овечки

Эту задачу предлагается решать жадно. Будем следовать следующему алгоритму. Создадим для каждого отрезка 2 пометки Position_v и MaximalPosition_v.

Position_v — соответствует позиции v в искомой перестановке.

MaximalPosition_v — соответствует максимальной допустимой позиции v в текущий. момент.

Пусть у нас также имеется счетчик count изначально равный 0 и множество необработанных вершин S. Будем действовать по следующему алгоритму.

1. Двоичным поиском ищем минимальное возможное расстояние между самыми удаленными соединенными овцами. Для фиксированного расстояния K проверяем существует ли перестановка.

2. Отсортируем все отрезки по возрастанию r_i.

3. Position_i = 0, 1 ≤ i ≤ n, MaximalPosition_i = n, 1 ≤ i ≤ n, current = 1, count = 0.

4. Выполнить count = count + 1, Position_current = count, удаляем current из S, если S — пустое, то требуемая перестановка найдена.

5. Перебираем все отрезки, которые соединены с current, и обновляем MaximalPosition_v = min(MaximalPosition_v, Position_current + K)

6. Строим множества S(count, j) = {v|MaximalPosition_v ≤ count + j}. Если для всех j ≥ K - count + 1 выполнено |S(count, j)| ≤ j то переходим к шагу 7, иначе выводим, что искомой перестановки не существует.

7. Ищем минимальное j такое что |S(count, j)| = j. Выбираем оттуда вершину с наименьшим r_i и берем ее в качестве нового значения current, переходим к шагу 4.

Сначала обоснуем время работы представленного алгоритма. Зафиксируем расстояние K (всего будет 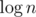итераций с фиксированным K).

Заметим, что шаги с 4 по 7 в худшем случае выполняются ровно n раз (каждый раз размер множества S уменьшается на 1). Каждый из шагов можно реализовать так, чтобы он выполнялся за O(n). Самый сложный шаг — это шаг 6. Но заметим, что нам не требуется явно строить эти множества, достаточно знать лишь их размеры. А это мы можем сделать за линейное время, просто посчитав сколько существует таких элементов, что MaximalPosition_v = i. Обозначим это число через C_i — тогда размер множества S(count, j) равен C₁ + C₂ + ... + C_{count + j}, что легко подсчитать при помощи массива частичных сумм.

Обоснуем теперь корректность алгоритма. Если алгоритм расставил позиции для всех вершин, то очевидно, что имеет требуемую перестановку. Предположим, что алгоритм заканчивает свое выполнение до того, как мы расставили все позиции, покажем, что тогда не существует искомой перестановки. Есть алгоритм закончил свое выполнение, это означает, что для некоторого count (рассмотрим найменьшее такое count), что есть такое j₀, что |S(count, j₀)| > j₀ на этом шаге. Покажем, что тогда |S(count, k)| > k. Докажем это от противного. Предположим, что это не так. Из определения count имеем |S(count - 1, j)| ≤ j для всех j ≥ k - count + 2. Тогда |S(count, j)| = |S(count - 1, j + 1)| - 1 ≤ j для всех j ≤ k - 1. При этом, S(count, j) = S(count, k) для k ≤ j < n - count = |S(count, j)| = |S(count, k)| ≤ j. В итоге |S(count, n - count)| = n - count. Тогда |S(count, j)| ≤ j для всех j, следовательно имеем противоречие. Значит, алгоритм преращает свою работу на шаге 6, |S(count, k)| > k. Это означает, что существует как минимум k + 1 вершина, которая до сих пор не имеет назначенной позиции после вершины, которая была отмечена как count. Значит, одна из вершин в S(count, k) должна быть с Position как минимум count + k + 1. Но все вершины в S(count, k) соединены с как минимум одной вeршиной с Position ≤ count. Следовательно, получаем, что искомомй перестановки не существует.

Разбор задач был подготовлен sdya и Seyaua.