- Contest Link: Programming Contest #1 (Chapter 'Ramayan')
- Problem Setter: Pallove
We know that:
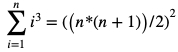
So, one of the best ways to create the array A of length n, is:
A[i]=i, where 1<=i<=n
Time Complexity: O(n), per test case.
Space Complexity: O(1), per test case.
#include<bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
for(int i=1;i<=n;++i)
cout << i << " ";
cout << '\n';
}
return 0;
}
-/-/-
- Problem Setter: Pallove
Bitwise-XOR of any number, X with 0 is equal to the number itself (X).
So, if we set the first element of the Array A as X, and the next K-1 elements as 0, then we will have the XOR of first sub-array of length K, equal to X, which is required.
XOR(A[0],...,A[K-1]) = X
Now, if we set A[K] as A[0], then we will have XOR(A[1],...,A[K]) = X
Similarly, if we set A[K+1] as A[1], then we will have XOR(A[2],...,A[K+1]) = X
And continuing so, we can observe that the general formula can be described as below:
A[i] = X, when i%K==0 and 0<=i<=N-1
A[i] = 0, when i%K!=0 and 0<=i<=N-1
Time Complexity: O(N), per test case.
Space Complexity: O(K), per test case.
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--)
{
ll n,k,_xor;
cin >> n >> k >> _xor;
vector<ll> ans(k,0);
ans[0]=_xor;
for(int i=0;i<n;++i)
cout << ans[i%k] << " ";
cout << '\n';
}
return 0;
}
-/-/-
- Problem Setter: Pallove
Let DP[i][j] denote the number of possible arrays, where i denotes the Last (Smallest) number in the Array, and j denotes the Size of the Array.
If the size of the array is 1, no matter whatever is the value of i, the following equation will always be true:
DP[i][1] = 1
Observe here that, the last (smallest) element of array of size j will always be less than or equal to last (smallest) element of array of size j-1.
Using this observation, we can generalise the DP table as follows:
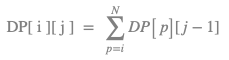 where
where 1<=i<=N and 2<=j<=K.
The above equation takes O(N*N*K) time, for calculating the whole DP Table.
So, we will use Suffix Sums, to calculate the DP Table, using the above formula, in O(N*K) time.
Time Complexity: O(N*K)
Space Complexity: O(N*K)
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define endl '\n'
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n,k;
cin >> n >> k;
vector<vector<int>> dp(n+1,vector<int>(k+1));
for(int i=1;i<=n;++i)
{
dp[i][1]=1;
}
for(int i=n;i>=1;--i)
{
for(int j=2;j<=k;++j)
{
if(i==n)
dp[i][j]=dp[i][j-1];
else
dp[i][j]=dp[i][j-1]+dp[i+1][j];
dp[i][j]%=1000000007;
}
}
ll ans=0;
for(int i=1;i<=n;++i)
{
ans+=dp[i][k];
ans%=1000000007;
}
cout << ans << endl;
return 0;
}
-/-/-
- Problem Setter: Pallove
Let’s create the two-dimensional array dis[node][deg], which stores the ancestor of node at distance 2deg.
If we fill this dis array, we can answer every query in lg(n) time, using Binary Lifting.
dis[node][0] = parent(node), for every node (except root)
dis[root][0] = -1, for root node.
So, now for deg from 1 to lg(n) and for each node,
dis[node][deg] = dis[dis[node][deg-1]][deg-1].
So, now, for each query node d, convert d into its binary representation and for every set bit in this binary representation, we replace node to dis[node][set-bit position from right], till the value of node doesn't become -1 or till all the set-bits of d are iterated.
Time Complexity: O((n+q)*(lg n))
Space Complexity: O(n*(lg n))
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define endl '\n'
vector<vector<int>> adj;
vector<vector<int>> dis;
void bfs()
{
queue<int> q;
q.push(0);
dis[0][0]=-1;
while(!q.empty())
{
int temp=q.front();
q.pop();
for(int u:adj[temp])
{
if(u!=dis[temp][0])
{
dis[u][0]=temp;
q.push(u);
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n,q;
cin >> n >> q;
adj = vector<vector<int>>(n);
for(int i=0;i<n-1;++i)
{
int x,y;
cin >> x >> y;
--x;
--y;
adj[x].push_back(y);
adj[y].push_back(x);
}
int logn = log2(n) + 1;
dis = vector<vector<int>>(n,vector<int>(logn+1));
bfs();
for(int i=1; i<=logn; ++i)
{
for(int node=0; node<n; ++node)
{
if(dis[node][i-1]!=-1)
dis[node][i]=dis[dis[node][i-1]][i-1];
else
dis[node][i]=-1;
}
}
vector<int> po(logn+1);
int temp=1;
for(int i=0;i<=logn;++i)
{
po[i]=temp;
temp=2*temp;
}
while(q--)
{
int node,d;
cin >> node >> d;
--node;
for(int i=logn; i>=0; --i)
{
if(d>=po[i])
{
d-=po[i];
node=dis[node][i];
}
if(node==-1)
break;
}
if(node==-1)
cout << -1 << endl;
else
cout << node+1 << endl;
}
return 0;
}
-/-/-
- Problem Setter: vok8
We will work using the "Binary (Bit) Representation" of all the variables.
Since, we need to find the minimum value of c, so, we will derive some conditions, for a particular bit position to be set (1) or reset (0) in the bit (binary) representation of c.
The conditions (For a particular bit position) are:
- The bit position of
a xor bisreset (0). (The bit position ofa&bis same) - The bit position of
disreset (0). - The bit position of
eisreset (0).
When all the above three conditions hold for a particular bit position, only then, that particular bit position of c will be set (1).
Hence, we derived the "Binary Representation" of required value of c, which will give the maximum value of the equation ((((a^b)|c)^d)|e).
So, just convert it into its Integer Representation, and that will be the required minimum value of c, for which the value of the equation ((((a^b)|c)^d)|e), will be maximum.
Time Complexity: O(1), per test case.
Space Complexity: O(1), per test case.
#pragma GCC optimize("O3")
#pragma GCC optimize("O1")
#pragma GCC optimize("O2")
#pragma GCC optimize("Os")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx2")
#pragma GCC optimization("unroll-loops")
#include <bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);
#define FO cout.tie(NULL);
#define FI cin.tie(NULL);
#define IN cin>>
#define OUT cout<<
#define loop(i,a,n) for(ll i=a; i<n; i++)
#define rloop(i,a,n) for(int i=a; i>=n; i--)
#define endl "\n";
#define pb push_back
#define mp make_pair
#define set_bits(a) __builtin_popcountll(a)
#define ll long long int
#define ld long double
#define vll vector<long long int>
#define pll pair<long long int, long long int>
#define mod 1000000007
#define M 998244353
using namespace std;
void vok()
{
FAST
FO
FI
#ifndef ONLINE_JUDGE
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
#endif
}
int main()
{
vok();
int t;
IN t;
while(t--)
{
ll a,b,d,e;
IN a>>b>>d>>e;
ll axb=a^b;
bitset<60> be(e), ans(0), bd(d), a_xor_b(axb);
bitset<60> a_xor_b_or_c(0);
loop(i,0,60)
{
if(!be[i] && !bd[i]) //Bit Position of 'e' and 'd' is Reset.
{
a_xor_b_or_c[i]=1; //We will want a_xor_b_or_c's Bit Position to be 1.
}
}
loop(i,0,60)
{
if(a_xor_b_or_c[i] && !a_xor_b[i])
{
ans[i]=1; //Set the c's bit position to 1
}
}
ll c=ans.to_ulong();
OUT c<<endl
}
return 0;
}
-/-/-
- Problem Setter: vok8
- Case-1: (n=0 or n=1)
You can directly find the nth term of the FX Sequence in O(1), using the given values of starting terms of the sequences, MFS and XS.
- Case-2: (n>=2)
The nth term of the MFS Sequence can be found using Matrix Exponentiation.
We have: MFS(x)= e*MFS(x-1) + f*(MFS(x-2)
In the form of Matrices, it can be written as:
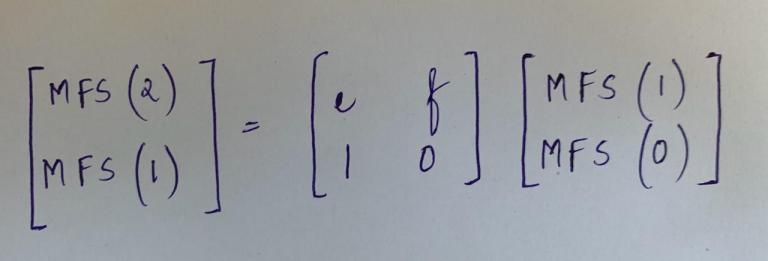
Hence,
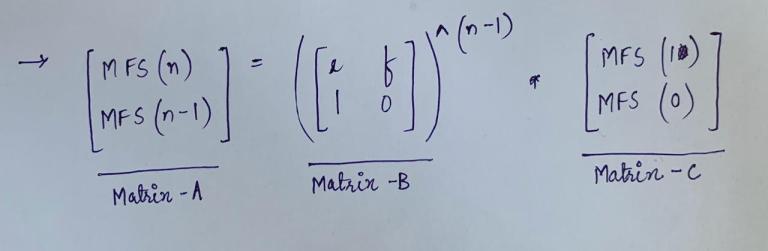
So, using Matrix Exponentiation, we will find the (n-1)th Power of the Matrix (which we call, Matrix-B), in O(lg(n-1)) time.
After that, we just have to multiply this Matrix-B with Matrix-C, to get Matrix-A.
At the end, the first term of Matrix-A (A[0][0]) will be the n'th (required) term of the MFS Sequence.
Writing the first 5-7 terms of the XS sequence, in terms of c and d, we get:
c, d, c^d, d^(c^d), d^(c^d)^(c^d), …
which is nothing but,
c, d, c^d, c, d, c^d, …
Hence, we can see that the sequence repeats itself, after every 3 terms.
Thus, the n'th term of this sequence can be found in O(1) time.
- When
n%3==0, thenXS(n) = c - When
n%3==1, thenXS(n) = d - When
n%3==2, thenXS(n) = c^d
Now, we found the n'th terms of both the sequences, MFS and XS, so, now, we can find the n'th term of the FX Sequence in O(1) time.
Time Complexity: O(lg(n)), per test case.
Space Complexity: O(1), per test case.
#pragma GCC optimize("O3")
#pragma GCC optimize("O1")
#pragma GCC optimize("O2")
#pragma GCC optimize("Os")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx2")
#pragma GCC optimization("unroll-loops")
#include <bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);
#define FO cout.tie(NULL);
#define FI cin.tie(NULL);
#define IN cin>>
#define OUT cout<<
#define loop(i,a,n) for(ll i=a; i<n; i++)
#define rloop(i,a,n) for(int i=a; i>=n; i--)
#define endl "\n";
#define pb push_back
#define mp make_pair
#define set_bits(a) __builtin_popcountll(a)
#define ll long long int
#define ld long double
#define vll vector<long long int>
#define pll pair<long long int, long long int>
#define mod 1000000007
#define M 998244353
using namespace std;
void vok()
{
FAST
FO
FI
#ifndef ONLINE_JUDGE
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
#endif
}
ll n,a,b,c,d,e,f;
void multiply(ll m1[2][2], ll m2[2][2])
{
ll res[2][2];
loop(i,0,2)
{
loop(j,0,2)
{
res[i][j]=0;
loop(k,0,2)
{
res[i][j]+=((m1[i][k]%M)*(m2[k][j]%M));
res[i][j]%=M;
}
}
}
loop(i,0,2)
{
loop(j,0,2)
{
m1[i][j]=res[i][j];
}
}
}
ll power(ll fib[2][2], ll n)
{
if(n==1)
{
return (((b*fib[0][0])%M)+((a*fib[0][1])%M))%M;
}
ll mul[2][2]={{e,f},{1,0}};
power(fib,n/2);
multiply(fib,fib);
if(n%2)
{
multiply(fib,mul);
}
return (((b*fib[0][0])%M)+((a*fib[0][1])%M))%M;
}
ll n_th(ll n)
{
ll fib[2][2]={{e,f},{1,0}};
return power(fib,n-1);
}
int main()
{
vok();
int t;
IN t;
while(t--)
{
IN n>>a>>b>>c>>d>>e>>f;
a%=M;
b%=M;
e%=M;
f%=M;
if(n==0)
{
ll mfs=a;
ll xs=c%M;
ll fx=mfs*xs;
fx%=M;
fx+=mfs;
fx%=M;
fx-=xs;
fx+=M;
fx%=M;
OUT fx<<endl
}
else if(n==1)
{
ll mfs=b;
ll xs=d%M;
ll fx=mfs*xs;
fx%=M;
fx+=mfs;
fx%=M;
fx-=xs;
fx+=M;
fx%=M;
OUT fx<<endl
}
else
{
ll xs;
if(n%3==0)
{
xs=c%M;
}
else if(n%3==1)
{
xs=d%M;
}
else
{
xs=(c^d)%M;
}
ll mfs=n_th(n); //Calculate n'th term of the MFS Seq.
ll fx=mfs*xs;
fx%=M;
fx+=mfs;
fx%=M;
fx-=xs;
fx+=M;
fx%=M;
OUT fx<<endl
}
}
return 0;
}
-/-/-
- Problem Setter: vok8
This question is based on Markov Chains. So, for this question, we have to first find the Transition Probability Matrix, from the Given Matrix.
Let’s call this Transition Probability Matrix as Matrix-P, and the given matrix as Matrix-A, where:
P[i,j] = A[i][j] / Sum(Row-i)
Using Markov Chain’s Finite State Transition Formula, we get that, the probability of going from Time State-i to Time State-j in exactly k steps (state changes) can be defined as:
Pk[i][j]
Since we have queries upto 10^5, and k is also upto 10^5. So, it is clear that the Brute-Force solution will give TLE.
So, basically, we will get the input of all the queries first, and then sort them in increasing order, with respect to the value of k.
While calculating the powers of the Matrix-P, we will save the answer for all the queries with k = Current Power of the Matrix.
At the end, we can print the saved answer (probability) for each query.
Time Complexity: O(max(k)*(n^3) + q)
Space Complexity: O(n^2)
Some links, to learn more about Markov Chains:
#pragma GCC optimize("O3")
#pragma GCC optimize("O1")
#pragma GCC optimize("O2")
#pragma GCC optimize("Os")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx2")
#pragma GCC optimization("unroll-loops")
#include <bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);
#define FO cout.tie(NULL);
#define FI cin.tie(NULL);
#define IN cin>>
#define OUT cout<<
#define loop(i,a,n) for(ll i=a; i<n; i++)
#define rloop(i,a,n) for(int i=a; i>=n; i--)
#define endl "\n";
#define pb push_back
#define mp make_pair
#define set_bits(a) __builtin_popcountll(a)
#define ll long long int
#define ld long double
#define vll vector<long long int>
#define pll pair<long long int, long long int>
#define mod 1000000007
#define M 998244353
using namespace std;
void vok()
{
FAST
FO
FI
#ifndef ONLINE_JUDGE
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
#endif
}
bool comp(const array<int,4> &a, const array<int,4> &b)
{
return a[0]<b[0];
}
int main()
{
vok();
int n;
IN n;
OUT fixed<<setprecision(8);
ld a[n][n];
ld rowsum[n];
memset(rowsum,0.0,sizeof(rowsum));
loop(i,0,n)
{
loop(j,0,n)
{
IN a[i][j];
rowsum[i]+=a[i][j];
}
}
ld probability_mat[n][n], tprobability_mat[n][n];
loop(i,0,n)
{
loop(j,0,n)
{
probability_mat[i][j]=a[i][j]/rowsum[i];
tprobability_mat[i][j]=a[i][j]/rowsum[i];
}
}
int q;
IN q;
vector<array<int,4>> queries(q);
//queries[i][0] -> k
//queries[i][1] -> x
//queries[i][2] -> y
//queries[i][3] -> index of the query (i)
int max_power_required=0;
loop(i,0,q)
{
IN queries[i][1]>>queries[i][2]>>queries[i][0];
queries[i][1]--, queries[i][2]--;
queries[i][3]=i;
max_power_required=max(max_power_required,queries[i][0]);
}
sort(queries.begin(),queries.end(),comp);
int curr_power=1;
int curr_ind=0;
ld ans[q];
while(curr_power<=max_power_required && curr_ind<q)
{
//Save the answer for queries, having k=curr_power
while(curr_ind<q && curr_power==queries[curr_ind][0])
{
ans[queries[curr_ind][3]]=probability_mat[queries[curr_ind][1]][queries[curr_ind][2]];
curr_ind++;
}
//Calculate P^(curr_power + 1)
ld temp[n][n];
loop(i,0,n)
{
loop(j,0,n)
{
temp[i][j]=0.0;
loop(k,0,n)
{
temp[i][j]+=(probability_mat[i][k]*tprobability_mat[k][j]);
}
}
}
loop(i,0,n)
{
loop(j,0,n)
{
probability_mat[i][j]=temp[i][j];
}
}
curr_power++;
}
//Answer all the queries
loop(i,0,q)
{
OUT ans[i]<<endl
}
return 0;
}











@admin please someone provide the Java code for the Lord Ram and XorOrXorOr Power problem as the editotial.
Editorial is not for direct solution. It is to give you some hint, or some guidance for the problem. Try in java yourself, and if you have some problem then ask it.
We can also solve Bharat and Possibilities by the concept of non negative integral solution.
For example if k = 10(length of array) and n = 3([1,3] — values can be used in array). Let c1 = count of 1 in the array, c2 = count of 2 in the array, c3 = count of 3 in the array, then c1 + c2 + c3 = 10
Irrespective of count of 1,2,3, whatever 10 elements we will select, needs no arrangement as only the reversed sorted one will be non-increasing.
So for the solution we need to find non negative integral solutions for c1 + c2 + c3 = 10 => (10+3-1)C(3-1) or (10+3-1)C(10)
In general we will get, c1 + c2 + ... + cn = k => (k+n-1)C(k) or (k+n-1)C(n-1)
Overall enjoyed the contest, kudos to setters :)
Woah!
"needs no arrangement as only the reversed sorted one will be non-increasing." Can someone explain this with a example?Please.
Let's say
k=3andn=5, and let's say:count(1)=2count(2)=2count(3)=1n = count(1) + count(2) + count(3) = 5For these values of
count(1),count(2), andcount(3), there is only one arrangement, which satisfies the condition of non-increasing order, and that arrangement is:3 2 2 1 1So, that statement means, there is only one possible arrangement for each unique permutation of
count(1),...,count(k).Thank you
I wrote this code using your approach,it is giving wrong answer. Can you point out what I did wrong?
The above part of your code, will cause overflow in the value of
res. Suppose the value ofresis less than(i+1), before this statementres /= (i + 1);. Hence, your code will lead you to a wrong value ofres.Instead, of doing what you have done in your code, maintain two
resvariables, and at the end, use the concept of Modular Inverse to calculate and return the value. You can check the below snippet, for more clarification.Can anyone suggest an alternative solution for the last problem?
I did some preprocessing. I used a dp like dp[n][n][K] (K is 1e5). Here dp[i][j][k] means the probability of going from ith state to jth state in exactly k steps.
We can do it like dp[I][j][k]= sum of (dp[i][u][k-1]*dp[u][j][1]) for all u from 1 to n because in (k-1)the step we can be in any state.
I am wondering can we decrease the 3rd dimension of dp here from K to log(K) as we do in binary lifting. We will just store the answer for only those steps which are the power of 2. Can somebody confirm it?
In case you want to check out my submission https://www.codechef.com/viewsolution/33157897.
I haven't fully read the editorial's approach. But here is what I did,
Consider dp[start_index][ending_index][number_of_jumps] as the probability of reaching from starting index to ending index with number_of_jumps. Here we can precompute this dp table and answer queries in O(1).
Now for jump = 1, it's simple dp[ i ][ j ][ 1 ] = grid[ i ][ j ]/sum[ i ] .
Now let's say for jump = x, we can calculate as following,
Consider we start from index 'i', want to reach 'j' in 'K' steps. Then try every possible ending index lets say 'x' we reach from 'i' in 'K-1' steps.
Then the transition is easy to see, Loop x from 1 to n.(i.e. every possible ending index we can reach in K — 1 steps)
dp[ i ][ j ][ K ] += dp[ i ][ x ][ K — 1 ] * dp[ x ][ j ][ 1 ].
I hope you get it, Here is my submission if you want to check: Submission
Hi bro, can i know how all of you came to know about this competition?
.
https://clist.by/
I used top down approach for Bharat and Possibilities.But I got TLE . dp[val][ind]- tells number of ways for placing val as first element with array of size n-ind
Can any1 optimize my code
You did not declare mod
Hey, your code seems to be
O(N*N*K), hence it is giving TLE.Use Suffix Sums, to reduce your code's complexity to
O(N*K). (Also, mentioned in the Editorial)PS: You can check that your solution is
O(N*N*K), and notO(N*K), by maintaining a globalcountvariable, and just increment that variable in the 'for' loop of your recursive function, and then check the value ofcountfor any values ofNandK.I hope, it helps!
How to use suffix sums in this top-down approach case? I get it my solution is O(N*N*K)
Run the above code for
N=2000andK=2000, you will get the value ofcounttas:countt = constant * N * N * KHence, showing up that your code runs in
O(N*N*K)Time, which is bound to give TLE.I put up
counttvariable's idea, just to verify the complexity of your code.I get that . Actually my question was how to use suffix sums in this top down approach?
Yes, I actually did same but couldn't optimize it so I had to write bottom up dp. Can anyone help?
You can let $$$dp_{ij}$$$ denote the number of ways to get a sequence of length $$$i$$$ such that the last element is at least $$$j$$$. Then you get an $$$O(1)$$$ recurrence relation. https://www.codechef.com/viewsolution/33181662 I'm using $$$n$$$ as the length and $$$[1,k]$$$ as the range.
Nice solution!!
One doubt, why didn't we take the recurrence relation as
dp[n][k]=(solve(n-1, k+1)+solve(n-1, k))%p ?
The numbers of sequences of length $$$n$$$ ending with $$$k$$$ is $$$dp_{(n-1)(k)}$$$, because after any number greater than $$$k$$$, I can write a $$$k$$$. So the first term is the number of ways to get a sequence of length $$$n$$$ that ends with $$$k$$$, and the second term is the number of ways to get a sequence that ends with something larger than $$$k$$$, by the definition of the dp.
can anyone explain this recurrence in bharat and possibilities dp[i][j]=dp[i][j-1]+dp[i+1][j] for this i don't understand the second term this: dp[i+1][j]
and also can't we also iterate from 1 to n for(int i=n;i>=1;--i) { for(int j=2;j<=k;++j) { if(i==n) dp[i][j]=dp[i][j-1]; else dp[i][j]=dp[i][j-1]+dp[i+1][j];/* this recurrence */ dp[i][j]%=1000000007; } }
If we see at dp formula it says dp[a][j] = sum(dp[i][j-1]) where i from a to n.
Now for i=n
dp[n][j] = dp[n][j-1]
So the value of dp[n][j] = dp[n][j-1]_______(eq-1)
And now we have i=n-1
So dp[n-1][j] = dp[n-1][j-1] + dp[n][j-1]
But dp[n][j] = dp[n][j-1] from eq1.
dp[n-1][j] = dp[n-1][j-1] + dp[n][j]
Or dp[n-1][j] = dp[n-1][j-1] +dp[n][j-1]________(eq-2)
And now if we have i = n-2
So dp[n-2][j] = dp[n-2][j-1] + dp[n-1][j-1] + dp[n][j-1]
But dp[n-1][j-1] + dp[n][j-1] = dp[n-1][j] (from eq-2)
So now dp[n-2][j] = dp[n-2][j-1]+dp[n-1][j]
So in general dp[i][j] = dp[i][j-1] + dp[i+1][j]
In Laxman and maths, one can solve by printing n for n times too, which will satisfy the given equation as sum of array = n*(n^3) = n^4 which is square of n^2.
Great i didn't think that way.
Can someone point out problem in this, It is giving wrong answer. question:- Luv Kush and FX Sequence
a, b, c, d, e, f are already of the order of 10^18, better take modulo before multiplying.