311A — The Closest Pair
P.S. I feel really guilty that I've made an awful mistake on the checker.
We read the pseudo code carefully. If we ignore "break", tot will be up to 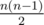 .
.
Consider whether we can make such inequality d ≤ p[j].x - p[i].x is always false. The obvious way is to make all points' x coordinates the same. And we can just choose n distinct numbers to be all points' y coordinate.
Thus the problem is solved.
311D — Interval Cubing
Consider a number x. If we apply an assignment x = x3, x becomes x3. If we apply such assignment once more, we will get (x3)3 = x32. If we apply such assignment k times, we will get x3k.
Thus, we can get such a sequence a0 = x, a1 = x3, a2 = x32, ..., ak = x3k, ....
Consider a prime p. From Fermat's Little Theorem, we can get xp - 1 = 1(mod p). Further more, we can get xy = xymod(p - 1)(mod p), here a mod b means the remainder of a divided by b.
Fortunately, 348 = 1(mod (95542721 - 1)), thus, x3k = x3kmod48(mod p). In other words, ak = ak + 48, which means the cycle of the sequence is T = 48.
Let's come back to the topic. Each time we run a 1-type query, for every i in the range [l, r], we apply such an assignment ai = ai3. At any moment some i has been applied 48 times such assignments, we can consider this i hasn't been applied any assignments before.
We can use segment tree to solve this problem. Every node of the segment tree maintains some information: the times that we applied assignments in the node's whole range(it's a lazy tag), current sum of the node's corresponding range and the sum of the node's range after we applied assignments k(1 ≤ k < 48) times.
In such a way, we can solve the problem in O(n·T + q·T·logn) time.
If you do not realize how to maintain the segment tree clearly, you can view the code 3782263.











Could you please explain the structure of segment tree again. I am not able to figure out even after trying a lot ??
I have figured out by working through your code. :)
what is "x" here in p[j].x or p[i].x ?.the x-coordinate of which point ?? and d is the distance between which point ?
Ahah?? I think the problem statement has declared clearly and every variable is corresponding.
how can we get x^y = x^ymod(p - 1)(mod p)????
From Fermat's Little Theorem:
When p is prime, x^(p-1)≡1 (mod p)
Let's define S as quotient of y/(p-1).
So,x^y≡{x^(p-1)}^S*x^y mod(p-1)≡1^S*x^y mod(p-1)≡x^y mod(p-1) (mod p)
It seems that the tree's nodes don't need to maintain the information "current sum of the node's corresponding range", for we can use lazy tags "locate" the current sum on the array which maintains the information "the sum of the node's range after we applied assignments k times". Like this: ans+=sum[now][lazy[now]];
how can we get x^y = x^ymod(p - 1)(mod p)????
see http://en.wikipedia.org/wiki/Fermat's_little_theorem