Hi! I'm now thinking about calculate geometric sum: 1+a+a^2+..+a^n mod m where a,m,n are 64-bit integer. I transform 1+a+a^2+...+a^n mod m=(a^(n+1)-1)/(a-1) mod m but a new problem appear: when gcd(a-1,m)>1 it seem impossible to find t such that t*(a-1) mod m=1. Any hint for this problem?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/20/2025 22:31:40 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











You can use the same idea as in binary exponentiation. Just calculate this sum together with an + 1 and you can easily write down formulas for transitions.
S = ( 1+a+a^2+...+a^(sqrt(n)-1) )%m; // sqrt(n) max that sqrt(n)*sqrt(n)<=n
t= (a^sqrt(n))%m;
ans=1;
for(int i=0; i<sqrt(n); i++) ans = ((ans*t)+S)%m;
for(int i=0; i<(n- sqrt(n)*sqrt(n); i++) ((ans*a)+1)%m;
You looked like liverpool FC fans!!!I am Kopite too....It's so wanderful
YNWA!
It can also be done using matrix exponentiation: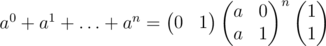
This breaks a butterfly upon a wheel.
Tastes differ.
Can you give some links to editorials or some books which can help to improve skill of seeing this kind of "matrix patterns"? Or this is just your own experience?
I use the following: imagine you have some loop which alters several variables in linear way, for example:
Then let's imagine that we have one row vector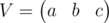 instead of three variables. Each iteration of loop alters this vector in some linear way, thus, we can represent one iteration as a matrix:
instead of three variables. Each iteration of loop alters this vector in some linear way, thus, we can represent one iteration as a matrix: 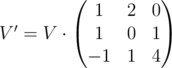
After than we can easily simulate any amount of loop's iterations in logarithmic time.
I use almost the same idea as yeputons: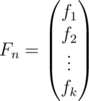
We have vector
Lets construct such matrix A that Fn + 1 = AFn.
Then Fn = AnF0.
In this case, f1 = an, f2 = S(n):

In order to better understand this, it is useful to construct such matrices for these sums: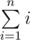 ,
,  ,
, 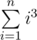 ,
, 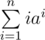 ,
,  ,
, 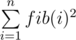 .
.
fib(i) — i-th Fibonacci number.
seems like we can generalize this formula: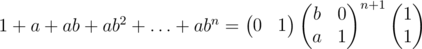
Looks like you have a problem with modulus arithmetics and division. As far as it is simple to do addition and multiplication in modulus arithmetics, it is not obvious how to do division. Have a look at first comment to this post It says that is modulus is a prime number and you want to calculate (a / x) MOD m you can calculate inverse element inv = x m-2 and then multiply a * inv
It's possible to perform the calculation of an + 1 - 1 modulo m * (a - 1) and then perform the division by a - 1. The proof of correctness goes into the Chinese Remainder Theorem.
m*(a-1) may exceed the limitation of 64-bit integer