This is the editorial for the Unofficial Div 4 Round #2 by ssense SlavicG.
We hope everyone had fun and enjoyed the contest!
Video Editorial by demoralizer
Problem A — Catching the Impostor.
Solution using frequency array:
Initialize an array of length $$$n$$$ with all the elements 0. This will be our frequency array. For every element we have in our list, we increase its frequency by one in the frequency array, $$$freq[arr[i]]+=1$$$. After we do this, we iterate through the frequency array and see how many elements have a frequency higher than 0 (it means they were mentioned in the list), let this number be $$$cnt$$$. Now if $$$cnt = n-1$$$ them we know for sure that who is the impostor, because all the other people are mentioned in the list. If $$$cnt ≠ n-1$$$ then we can't for sure know who is the impostor, so the answer is no.
Solution using set:
We introduce all the elements of the list in a set. A property of a set is that it doesn't contain a multiple elements of the same value. We just need to see how big the size of the set (how many distinct people are on the list). If this size is equal to n-1 then the answer is "YES", else "NO".
#include "bits/stdc++.h"
using namespace std;
int main()
{
set<int> s;
int n, m;
cin >> n >> m;
for(int i = 0;i < m;i++){
int x;
cin >> x;
s.insert(x);
}
if(s.size() == n - 1){
cout << "YES";
}else{
cout << "NO";
}
}
Problem B — Rabbit Game
We iterate from the start and see how many carrots the first rabbit can eat, let this be $$$cnt_1$$$. We iterate from the end to see how many carrots the second rabbit can eat, let this be $$$cnt_2$$$. If $$$cnt_1 + cnt_2 > n$$$ then some carrots will be eaten by both rabbits, but this is not possible because they stop whenever they meet. The answer is $$$min(n, cnt_1+cnt_2)$$$.
#include "bits/stdc++.h"
using namespace std;
int main()
{
int n;
cin >> n;
int a[n];
for(int i=0;i < n;i++)
cin >> a[i];
int Rabbit1 = 1;
for(int i = 1 ;i < n;i++)
{
if(a[i] >= a[i-1]){
Rabbit1++;
}else{
break;
}
}
int Rabbit2 = 1;
for(int i = n-2;i>=0;i--)
{
if(a[i] >= a[i+1]){
Rabbit2++;
}else{
break;
}
}
cout << min(n , Rabbit2 + Rabbit1);
}
Problem C — Similar Arrays
The array we make should consist only of the median of the array (the middle element after sorting the array). If $$$n$$$ is even and there are two medians, both medians and all values between them are optimal choices.
The median is an optimal choice because if $$$x$$$ (any element from the array) is smaller than the median, the sum becomes smaller by increasing $$$x$$$, and if $$$x$$$ is larger than the median, the sum becomes smaller by decreasing $$$x$$$. Hence, the optimal solution is that $$$x$$$ is the median.
#include "bits/stdc++.h"
using namespace std;
int main()
{
int n;
cin >> n;
int a[n];
for(int i = 0;i < n;i++){
cin >> a[i];
}
sort(a,a+n);
long long ans = 0;
int median = a[n/2];
for(int i = 0;i < n;i++){
ans += abs(median - a[i]);
}
cout << ans;
}
Problem D — Sanda's Job
We need to find if the difference between $$$n$$$ and $$$x$$$ is also a permutation of $$$x$$$'s digits. There are many ways to do this, and our solution is to transform $$$x$$$ and $$$n-x$$$ into strings, then sort the strings and see if they are equal. This is possible in C++ using to_string(int value) function.
#include "bits/stdc++.h"
using namespace std;
int main()
{
long long n,m;
cin >> n >> m;
m-=n;
if(m <= 0){
cout << "NO";
return 0;
}
string s = to_string(n);
string k = to_string(m);
sort(s.begin(), s.end());
sort(k.begin(), k.end());
if(k==s){
cout << "YES\n";
}else{
cout << "NO\n";
}
}
Problem E — Count Substrings
We iterate through string $$$s$$$, and whenever we encounter a substring $$$t$$$, we add to the answer the number of unique substrings we can make using it. We can calculate this with the formula (number of characters since the start of the last encounter)$$$\cdot$$$(the number of characters until the end of the string). This is because the start of the substring must be between the start of the last $$$t$$$ substring in $$$s$$$ and the start of the $$$t$$$ substring just encountered(so we don't double count previous substrings). The end must be between the last element of this $$$t$$$ substring and the last element of string $$$s$$$.
#include "bits/stdc++.h"
using namespace std;
int main()
{
string s, t;
long long n;
cin >> n >> s >> t;
long long l = 0;
long long ans = 0;
for(int i = 0; i < n-1; i++)
{
if(s[i] == t[0] && s[i+1] == t[1])
{
long long from = i-l+1;
long long to = n-(i+1);
ans += from*to;
l = i + 1;
}
}
cout << ans << endl;
}
Problem F — Game on Grid
we can find the answer by looking at the cases depending on n % 4, or we can use a formula. In either case, below is proof of why it works.
Let's solve this problem for a more general case of rectangular grid $$$n \times m$$$, with rows and columns counted starting from $$$1$$$. Let even cell denote a cell with both even coordinates, all shown on the right drawing.
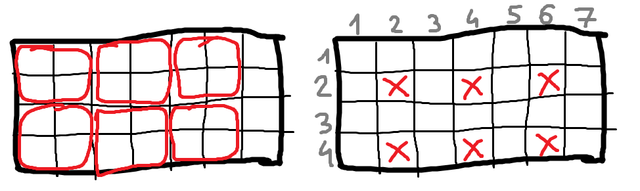
Consider $$$X = \left \lfloor{ \frac{n}{2} }\right \rfloor \cdot \left \lfloor{ \frac{m}{2} }\right \rfloor$$$ squares with even bottom-right corners, as shown on the left drawing. Since the squares are disjoint and Bob colors only one cell per move, he can block Alice from at most one of those $$$X$$$ squares per turn. Alice starts so she can color $$$\left \lceil{ \frac{X}{2} }\right \rceil$$$ of the $$$X$$$ squares and thus guarantee the score of $$$4 \cdot \left \lceil{ \frac{X}{2} }\right \rceil$$$, no matter what Bob does.
There are $$$X$$$, even cells. Alice covers exactly one of them per move because any possible $$$2 \times 2$$$ square contains exactly one even cell. If Bob colours an even cell every time too, they will spend $$$X$$$ moves in total to block all even cells, and then Alice won't be able to move. This way Bob can guarantee that Alice makes at most $$$\left \lceil{ \frac{X}{2} }\right \rceil$$$ moves and gets the score of $$$4 \cdot \left \lceil{ \frac{X}{2} }\right \rceil$$$.
Alice can make her score to be at least $$$4 \cdot \left \lceil{ \frac{X}{2} }\right \rceil$$$ and Bob can make Alice's score to be at most $$$4 \cdot \left \lceil{ \frac{X}{2} }\right \rceil$$$. Her score is thus exactly:
Bob's score must be $$$B = n \cdot m - A$$$ because he can always finish the whole grid. We can compare $$$A$$$ with $$$B$$$ to get the answer.
Alternatively, you can consider cases depending on $$$n \bmod 4$$$ and $$$m \bmod 4$$$. For example, if $$$n = m = 4 \cdot k + 1$$$ then $$$X = 2k \cdot 2k = 4 \cdot k^2$$$ so $$$A = 4 \cdot (2 \cdot k^2) = 8 \cdot k^2$$$. That's smaller than half of full grid area $$$(4 \cdot k + 1)^2$$$ so Bob wins.
(We don't claim anything about the optimal moves of Alice and Bob. In particular, Alice doesn't have to choose exactly those squares marked on the drawing.)
#include "bits/stdc++.h"
using namespace std;
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
if(n%4==2){
cout << "Alice\n";
}else if(n%2==0){
cout << "Draw\n";
}else{
cout << "Bob\n";
}
}
}
#include "bits/stdc++.h"
using namespace std;
int main()
{
long long n;
cin >> n;
long long cover = ((n / 2) * (n / 2) + 1) / 2;
long long as = 4 * cover;
long long bs = n * n - as;
if (as == bs) cout << "Draw\n";
else if (as < bs) cout << "Bob\n";
else cout << "Alice\n";
}










great round! thanks for setting!
How to solve problem E if we had subsequences instead of substrings?
PS: I was trying to solve the problem for subsequences the whole time :(
For every starting position $$$L$$$, find the next occurrence of $$$t[0]$$$. After that new position, find the next occurrence of $$$t[1]$$$. That's the earlier possible value of $$$R$$$ (but any bigger $$$R$$$ will also work for our $$$L$$$).
Sorry that the statement and samples weren't clear enough.
Thanks for the explanation :)
this is quite similar but a little more interesting.
E was not clear in the statement whether it is substring or subsequence, I was first solving the latter case.
Did you notice the problem name?
You didn't get, you count substrings but it is not clear whether you should care about t as a subsequence or as a substring.
Ah cool, got it now. Sorry!
Sorry for the confusion
can you give me inbuilt fn on how to convert a string to integer value?
stoi(x)— converts stringxto integer and returns it.I don't recommend this, because it won't work for long long.
Use
stoll(x)for long longThanks man, did not knew about this.
http://www.cplusplus.com/reference/string/stoi/
thank y'll
string s="sss"; int x=stoi(s); cout<<x; I executed this simple code but getting command terminated!help
try with strings "123", "10123" or others. Stoi converts strings to integers but the string has to be a number (formed only of digits).
Cool contest, F was a pretty interesting task!
Thank you!
Is it possible to make test cases available? I want to see which tc got me wrong ans.
Help: For C, I took the middle two elements for n > 3 and calculated its mean, and took that as my x (the number to subtract from every number in the array), I think it is correct but I got WA on tc 52. I can provide the code if needed.
Write from your main account and provide a submission link. It's then easier to see the test.
Submission
Assume a={1,2,3,4,5}
Then first=3, second=2, value=2... wrong answer. You can ignore second and value, just use first.
I enjoyed the Contest, please do make more like it
Could you write the editorial's URL at contest top page? https://codeforces.net/gym/102873
It will be more helpful! :)
Thanks to problem setters, testers and everyone involved. It was a great contest. Keep making contests like these. I am up for becoming one of the testers if needed.
great editorial.thank you for making this.
For problem D, I took the difference of the two numbers a and s and kept a count of digits 0 through 9 in a and x(the difference) and compared them, but it's wrong. Can anyone please help?
My code: https://codeforces.net/gym/102873/submission/99581289
You have to put " return 0; " after printing answer for x<=0 else you will print NO 2 times.
I believe if you swap problems B and F nobody will notice and more people will have solved F.
For E, what if the string T has length N. Now can it be solved in $$$O(N)$$$?
Also, can you please make the submissions of other participants visible for the contest.
Yes, you would need to start from any pattern matching algorithm like KMP or hashing.
Sadly, it's impossible to make submissions in GYM visible. Maybe it's time to change this, MikeMirzayanov? For educational purposes.
hey Errichto, can you plz let us know how to approach problem F. I tried to solve it during contest, but it was failing. here it the code that i submitted : https://ideone.com/Db95wz.
Thanks in advance !!
Have you looked at the editorial for the problem? In your approach Alice wins only if n = 2 which is not right. Check the proof for a better understanding.
No need to tag me. Authors could help you as well.
The solution is described in the editorial. Your solution apparently prints different answers so it's wrong. In particular, Alice can win for big values of $$$n$$$ like 6 or 10.
Problem E is the best problem from the whole didn't see such good problem in a while.
ok, mathbot
Great round! Please set more rounds like this.