Hi Everyone,
TCO20 Algorithm Finals – the most awaited Topcoder tournament of the year is almost here. Will tourist reign supreme or does someone else in the group have what it takes?
16 top-rated members will be competing in the next few weeks for the ultimate title of Topcoder Open.
Here’s how the semifinal rounds look:
Semi-Final 1 Group

Semi-Final 2 Group

Live Broadcast
TCO20 Algorithm Rounds will be broadcasted live and you’ll be able to listen to the amazing hosts Errichto and Lewin during the contest as they will explain the problems, do live commentary, and show you the competitors’ screens. They will be joined by some amazing guest competitors on each broadcast and also there are some exciting post match interviews planned too.
Find the full schedule with all the details and signup links to the event here.
TCO20 Special Rookie SRM with Prizes
If you are new to Topcoder, we are also organising an interesting educational beginner contest with prizes after Semifinal 2:
TCO20 Special Rookie SRM
Wednesday, November 18, 2020 13:00 UTC-5
The Rookie SRM is open to everyone and has some special cash prizes. It will only be **rated** for members who have competed in equal to or less than 5 rounds or if their current rating is less than 800 rating points.
Prizes:
- 1st :: $300
- 2nd :: $200
- 3rd :: $100
- $25 for 5 other random participants
- Topcoder T-shirt for Top 30
- *All prizes are only for members who are eligible to be rated.
Stats — Algorithm Finalists Head to Head
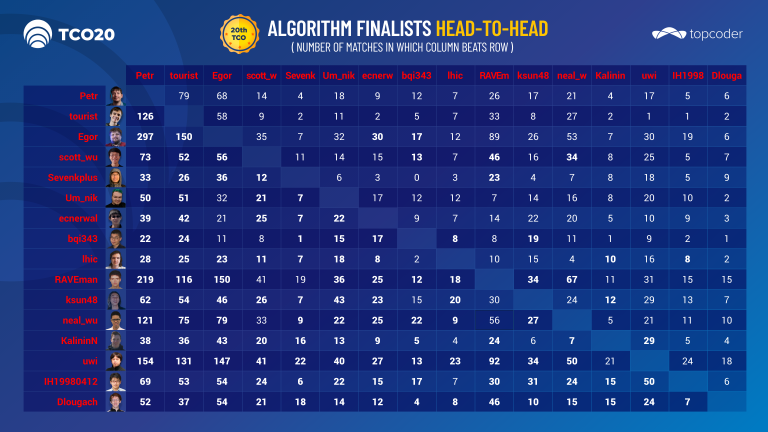
We hope to see you there!











Is it necessary for spectators to register somewhere? Why not just make a Youtube broadcast?
As far as I know, there will be Youtube broadcast too but there is no link yet. You should register to Hopin event if you want to ask us questions during a stream like "what about N=1" or "can you show tourist's screen".
It will be broadcasted on
(I will update the Youtube link as soon as it is set)
However as Errichto said — You should register to Hopin Event if you want to ask questions during the stream. :)
if their current rating is less than 800 rating points.
Can you please make it 1845 instead?
Thanks and Regards,
Aryan Choudhary
hmehta, can we have official final standings together with decisions regarding challenges, finals quota and everything somewhere?
Hey KAN, The Final results were adjusted and updated: https://community.topcoder.com/stat?c=round_overview&er=5&rd=18398
The announcement was made on the broadcast and we will also be doing an official post about it today later in the day on the Finalists Forum and also on the General Forums.
I fixed some redundancy issues in my 500, and now I pass systests in 640 ms and 160 MB. But on my challenge case, my code takes over 20 seconds and several GB.
I'm very curious now what the reference solution is. Is it possible that my challenge requests timed out because my test case timed out the reference solution?
Lewin confirmed that my test case breaks the reference solution. That explains why my challenges on Jacob kept getting "Your request timed out."
Here's the test case:
The main idea is that the numbers 1-26 are all independent and set up at an odd distance, but they each affect the numbers 27-52 differently. The test case is a shuffled and slightly modified version of the following test case:
This way, after the first 26 choices there are exactly $$$2^{26}$$$ different states. The number of states peaks at about $$$10^8$$$, for the prefix of length 28.
If TopCoder really managed to have problems with a model solution on finals two years in a row, I am quite impressed.
I quite enjoyed that vibe "we have solved medium pretty much immediately, what are they doing, why are they going for hard" on stream. Yeah, we just decided that 2^26 * 26 is a bit too much and setter wouldn't go out of his way to set limitations to 52 if he wanted such solutions to pass.
Let $$$K$$$ be a constant. For some $$$k \leq K$$$, let $$$F(n, k)$$$ be the number of ways to assign each edge of a complete graph with $$$n$$$ nodes a weight in $$$[1, K]$$$, such that the all the edges in its unique MST (say $$$T$$$) have weights $$$ \leq k$$$. We'll prove that $$$F(n, k)$$$ for a fixed $$$n$$$ is a polynomial in $$$k$$$ of degree $$$\binom{n}{2}$$$.
Consider the forest obtained by removing all edges of $$$T$$$ with weight equal to $$$k$$$. Let the component sizes be $$$x_1, x_2, \ldots, x_r$$$ (such that the component containing $$$1$$$ has size $$$x_1$$$, the component containing the smallest node not in the component of node $$$1$$$ has size $$$x_2$$$, so on). There are $$$\binom{n-1}{x_1-1}\binom{n-x_1-1}{x_2-1}\binom{n-x_1-x_2-1}{x_3-1}\ldots$$$ ways to choose these components. There are $$$u = \binom{n}{2} - \sum \binom{x_i}{2} - r + 1$$$ non-MST edges with endpoints in different components. These $$$u$$$ edges must have weight strictly greater than $$$k$$$ (else $$$T$$$ won't be an MST or it won't be the unique MST). So, we need to multiply by $$$(K-k)^u$$$. Now, in each component, there must be a unique MST and weights on MST must be $$$< k$$$. So, we need to multiply by $$$\prod F(x_i, k - 1)$$$. Also, we can connect these components with weight $$$k$$$ MST edges in $$$\displaystyle n^{r-2} \prod x_i $$$ ways (generalized cayley's theorem).
So, overall,
F(n, k)= \dfrac{1}{n^2} \displaystyle \sum_{\sum x_i = n} \left [ \left ( \binom{n-1}{x_1-1} \binom{n-x_1-1}{x_2-1}\ldots \right )(K-k)^{\binom{n}{2} + 1 - \sum (\binom{x_i}{2} + 1)} \prod (n x_i F(x_i, k - 1)) \right ]
$$$
$$$F(1, k) = 1$$$ is clearly a polynomial of degree $$$0$$$.
For any $$$n > 1$$$, if the number of components is greater than 1, all $$$ x_i < n $$$, and by induction $$$F(x_i, k-1)$$$ is a polynomial in $$$k$$$ of degree $$$\binom{x_i}{2}$$$. So, the overall degree would be $$$\binom{n}{2} + 1 - \sum (\binom{x_i}{2} + 1) + \sum \binom{x_i}{2} \leq \binom{n}{2} - 1$$$. So, $$$F(n, k) - F(n, k - 1)$$$ is a polynomial in $$$k$$$ of degree $$$\binom{n}{2} - 1$$$. $$$F(n, k)$$$ is the prefix sum of this polynomial and hence has a degree $$$\binom{n}{2}$$$.
We can find $$$F(n, k)$$$ for all $$$1 \leq n \leq N$$$, $$$1 \leq k \leq \binom{N}{2}$$$ using the recurrence above in $$$O(N^5)$$$ with a small constant and then use lagrange interpolation to recover $$$F(N, K)$$$.
Nice problem! I was close, I thought for some reason that edges not in MST in smaller parts should also be smaller than $$$k$$$, so I had to try $$$O(n^4)$$$ values for transition (to get wrong answer), but everything else is pretty much the same.
Finals will start in 25 minutes! Watch on Hopin or Twitch (https://www.twitch.tv/topcoder_official).
Awards Ceremony starting in 15 mins: https://app.hopin.com/events/topcoder-tco20-sat-sun-november-21-22/stages/20250454-6cec-4f54-9372-7a91a1244555
https://www.twitch.tv/topcoder_official
tourist aura?
Feeling sad for um_nik with um_nik and 69 others.