336A - Медведь Василий и треугольник
Пусть val = |x| + |y|. Тогда первая точка имеет вид (val * sgn(x), 0), а вторая — (0, val * sgn(y)), где sgn(a) — знак числа a. При необходимости нужно поменять точки местами.
Теперь поймем, почему это верно. Во-первых, заметим, что из условий x ≠ 0 и y ≠ 0 следует, что одна точка находится на оси OX, другая — на оси OY. Рассмотрим случай, когда x > 0 и y > 0 (остальные случаи рассматриваются аналогично). Построим треугольник с вершинами, указанными выше. Нужно показать, что точка (x, y) находится строго на границе треугольника, т.е. принадлежит отрезку, проходящему через точки: (x + y, 0) и (0, x + y) (если она находится внутри треугольника, то условие 5 задачи не будет выполняться). Через точки (x + y, 0) и (0, x + y) проходит прямая Y = - X + x + y. Подставив точку (x, y) вместо X, Y соответственно, получим, что точка (x, y) принадлежит прямой, проходящей через точки (x + y, 0) и (0, x + y). А так как x > 0 и x < x + y, то точка (x, y) принадлежит и отрезку между точками (x + y, 0) и (0, x + y).
336B - Медведь Василий и муха
Можно было итеративно посчитать все пройденное расстояние и поделить его на m2 в конце. Переберем стартовую окружность 1 ≤ i ≤ m. Нетрудно заметить, что до окружности с номером m + i мы дойдем за 2R. Далее если |j - i| = 1 то расстояние равно 
. До остальных окружностей расстояние посчитать нетрудно: слева у нас i - 2 окружности причем расстояние сумма расстояний до них равна сумме 
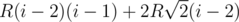. Аналогичная ситуация справа. 
336C - Медведь Василий и последовательность
Переберем красоту ответа по убыванию от 29 до 0. Попробуем найти для текущего значения красоты i такое подмножество, красота которого была бы равна i. Возьмем все числа, в двоичном представлении которых есть бит i. Возьмем побитовое И всех этих чисел. Если значение побитового И делится на 2i, то мы нашли искомое подмножество, иначе такого подмножества нет. Таким образом, получили решение за O(30n). Доказательство того, что данный алгоритм найдет оптимальный ответ, предоставлю читателю.
336D - Медведь Василий и красивые строки
Пусть any — любая строка из нулей и единиц, s + g — конкатенация строк, MOD = 1000000007.
Нетрудно заметить, что строка вида 1 + any всегда перейдет в 0, а строка 1 — в 1. Строка вида 01 + any всегда перейдет в 1, а строка 01 — в 0. Аналогично, строка вида 001 + any всегда перейдет в 0, а строка 001 — в 1, и так далее. На основе этих утверждений получаем описанное ниже решение.
Рассмотрим отдельно случаи, когда в строке ноль нулей или ноль единиц. Теперь переберем позицию i (в 0-индексации) первой единицы в нашей строке и определим, во что перейдет наша строка. Если она перейдет в то число, которое нужно нам, то добавим к ответу число C(cnt[0] + cnt[1] - i - 1, cnt[1] - 1), где C(n, k) — биномиальный коэффициент. Заметим, что использовать для вычисления биномиальных коэффициентов треугольник Паскаля нельзя, поскольку число n слишком большое. Подсчитаем массив fact[i] = i!%MOD, 
. Тогда C(n, k) = fact[n]inv(fact[n - i]fact[i]), где inv(a) — обратный элемент в кольце по модулю MOD. Так как модуль простой, то inv(a) = aMOD - 2. Для вычисления этой величины можно применить бинарное возведение в степень.
336E - Медведь Василий и покраска квадрата
Достаточно трудная задача. Будем считать динамику dp[lvl][op][cur][type] — количество способов зафиксировать на рисунке op треугольников, если у нас на рисунке 2lvl + 1 квадратов (cur, type — вспомогательные параметры). Ответом на задачу тогда будет число dp[n][k][0][2]k!. Поясним, что значат параметры cur, type. Параметр type отвечает за тип переходов, который мы будем производить, cur — количество использованных четвертей на рисунке (cur = 4 — 2 четверти, cur < 4 — cur четвертей). Следует отличать cur = 2, cur = 4, так как количество последовательных пар неиспользованных четвертей различно.
Теперь переходы. type = 2. Переберем количество пар (с учетом значения cur) последовательных четвертей, которые мы зафиксируем. Очень важно, чтобы эти пары не пересекались по четверти. (Таким образом, мы можем взять две пары только в случае cur = 0). Также зафиксируем некоторые одиночные четверти. Посчитаем количество способов выбрать соответствующие треугольники. И прибавим к текущему значению динамики dp[lvl][op - choosen][newcur][1] * cntwaystochoose. Более подробно можно изучить переходы type = 2. в моем решении. (calc(n, k, cur, type) — считает как раз dp[n][k][cur][type]).
Теперь type = 1. Теперь мы будет фиксировать треугольники по краям рисунка (количество квадратов на рисунке 2*lvl + 1). По краям рисунка имеются в виду треугольники помеченные крестиком на рисунке.
Переберем количество пар (с учетом значения cur) последовательных треугольников, которые мы зафиксируем. Очень важно, чтобы эти пары не пересекались по треугольнику. Также зафиксируем некоторые одиночные треугольники. Посчитаем количество способов выбрать соответствующие треугольники. И прибавим к текущему значению динамики dp[lvl][op - choosen][cur][0] * cntwaystochoose.
Теперь type = 0. Вновь фиксировать треугольники по краям рисунка (количество квадратов на рисунке 2*lvl). По краям рисунка имеются в виду треугольники помеченные крестиком на рисунке.
Зафиксируем некоторые одиночные треугольники. Посчитаем количество способов выбрать соответствующие треугольники. И прибавим к текущему значению динамики dp[lvl - 1][op - choosen][cur][2] * cntwaystochoose. База динамики: dp[0][0][cur][1] = 1, dp[0][cnt][cur][1] = 0, cnt > 0.
Насчёт остальных, может быть, еще и спорно, но вот Е точно сгодилась бы за Ediv1, а то и за F.
Это D по сложности в div 1, не более того
336C — Медведь Василий и последовательность
Почему именно 29-0 ? Не могу понять.
Потому что 230 уже больше чем 109
"Если значение побитового И делится на 2i" Правильно ли я понимаю, что в данной ситуации оно будет либо равным, либо будет меньше ?
Наличие i-того бита проверяется операцией И с 2^i ?
Извините за такие глупые вопросы.
Значение побитового И массива чисел не может быть больше максимума чисел.
Спасибо.
for Problem 336A, 4th condition is that the area of triangle should be minimum, for test case 1 (x=10,y=5) point 'A' should be A(0,10) and point 'C' should be C(20,0) which gives the smallest area of triangle ABC (0.5*20*10 = 100) but answer is given as point A(0,15) and C(15,0) which gives area of triangle as 0.5*15*15 = 112.5, please tell me what I m missing?
It's should be isosceles triangle.
The triangle needs to be Isosceles.
you have to choose such points so that other two angles i.e ACB and BAC should be 45 degree.If you chose other point then angle will be different.For example in first test case we are finding x1,x2,y1,y2 using trigonometry formula i.e. tanθ = perpendicular / base. Suppose D is point having coordinate x and y.From point D we make a perpendicular to line BC and AB and name these point as E and F resp.we know BE = x = 10 and FB = y = 5,we have to find EC (BC = BE + EC) ? , we use tan formula to get FB/EC = tanθ here θ = 45 degree so EC = FB = 5(tan 45 = 1); so x2 = BE + EC = 15; Similarly we find AF(AB = AF + FB), AF/BD(BD = BE = 10) = 1(tan45 = 1) so AF = 10; y1 = AF + FB = 15;
gridnevvvit May you please tell us the manner in which these geometric shapes are generated? I think they are really elegant.
The pictures are broken, please fix them.
In problem C: we have b1 and b2 and ... and bk = 0, is it an accepted answer? 0 mod n = 0 with any n.
For Problem B it is mention that experiment repeats for m^2 days. But in authors solution the experiment is running only for m days. Please tell me am i missing something..
Experiment is running m2 days. Authors calculate answer by using following idea. We fix some circle with index i (1 ≤ i ≤ m). After that we calculate sum of of distances to circles with indexes m + j (1 ≤ j ≤ m) by using formula.
in problem C you have written: after doing bitwise AND of all numbers whose ith bit is set, we have to divide it by 2^i. Can there be a case when it is not divisible by 2^i but divisible by for some other power of 2?
It is possible that the bitwise-AND result of numbers with the ith bit set to 1 might be divisible by 2^j, j!=i. But let us analyse what such j's can be.
Case 1: j>i. If the set chosen for i is such that the jth bit = 1 for all numbers in that set, then this set will indeed be divisible by 2^j. But, since we are iterating i from 29 to 0, this particular j (>i) would already have been considered and a set with equal or greater no. of elements as compared to the set corresponding to i would already have been found out.
Case 2: j<i. Again, since we are iterating i from 29 to 0, we need not consider the case that the result obtained by bitwise AND of the set corresponding to i will be divisible by 2^j since this will be checked in future iterations of i when it is decremented further till i=j. Here, we may end up with this same set only or perhaps an even larger set which is perfectly divisible by 2^j.
To sum up, though the set under consideration might be divisible by 2^j (j!=i), but we need not consider divisibility by j's != i since this has already been/will in future be checked. Hope, this clarifies the issue.