Если d = 0, то существует всего одно число, что 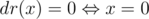 , поэтому, если k = 1, то ответ — 0, иначе — No solution.
, поэтому, если k = 1, то ответ — 0, иначе — No solution.
Если d > 0, то подоходящим числом, к примеру, являтся d × 10k - 1.
Асимптотика решения: O(1) + O(k) на вывод решения.
355B - Вася и общественный транспорт
Если мы купим билет четвертого типа, то больше ничего покупать не надо, по-этому ответ — min(c4, ответ из билетов первых трех типов).
Теперь, когда у нас нету билета четвертого типа, можно решать задачу независимо для автобусов и потом аналогично для троллейбусов.
Решая задачу только для автобусов, если мы купим билет третьего типа, то больше покупать ничего не надо, по-этому ответ равен min(c3, ответ из билетов первых двух типов).
Без билетов третьего типа можно решать задачу независимо для каждого автобуса. Таким образом, если мы купим билет второго типа, то потратим c2 бурлей, если же купим ai билетов первого типа, то потратим (ai × c1) бурлей. Таким образом, ответ для автобуса i — min(c2, ai × c1).
Собрав все вместе несложно получить следующее решение:
function f(x, k) {
res = 0;
for i = 1 .. k
res = res + min(c2, x[i] * c1);
return min(c3, res);
}
ans = min(c4, f(a, n) + f(b, m));
Асимптотика решения: O(n + m).
Переберем, сколько раз мы будем использовать операцию слева. Путь мы используем ее k раз, тогда понятно, что операциями слева мы заберем k первых предметов, а оставшиеся (n - k) предметов заберем справа. Тогда робот затратит sumLeft[k]·l + sumRight[n - k]·r энергии плюс некоторый штраф за одинаковые операции. Чтобы минимизировать этот штраф операции необходимо выполнять в порядке LRLRL ... RLRLLLLL ..., начиная с тех операций, которых больше. К примеру, если k = 7, n - k = 4, то выполнять операции надо в последовательности LRLRLRLRL LL. Таким образом нам надо будет заплатить штраф два раза (7 - 4 - 1).
sumLeft[i] — сумма первых i весов, sumRight[i] — сумма последних i весов.
Псевдокод решения:
ans = inf;
for i = 0 .. n {
curr = firstSum[i] * l + lastSum[n-i] * r;
if ( i > n - i ) curr = curr + (2i - n - 1) * Ql;
if ( i < n - i ) curr = curr + (n - 2i - 1) * Qr;
ans = min(ans, curr);
}
Асимптотика решения: O(n).
Будем говорить, что клетка (r, c) соответствует строке s, если существует корректный путь, заканчивающийся в клетке (r, c), которому соответствует строка s.
Найдем для строки s множество соответствующий ей клеток, назовем это множество состоянием. Одно состояние может соответствовать множеству разных строк. Перебрать все возможные строки мы не можем, так как их количество — 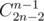 слишком большое, однако перебрать все состояния мы можем. Несложно понять, что все клетки соответствующие одной строке находятся на одной диагонали, таким образом количество различных состояний равно 21 + 22 + ... + 2n - 1 + 2n + 2n - 1 + ... + 22 + 21 = O(2n). В реализации состояние можно охарактеризовать номером диагонали (от 1 до 2n - 1) и битовой маской клеток, которые в него входят (2n).
слишком большое, однако перебрать все состояния мы можем. Несложно понять, что все клетки соответствующие одной строке находятся на одной диагонали, таким образом количество различных состояний равно 21 + 22 + ... + 2n - 1 + 2n + 2n - 1 + ... + 22 + 21 = O(2n). В реализации состояние можно охарактеризовать номером диагонали (от 1 до 2n - 1) и битовой маской клеток, которые в него входят (2n).
Из каждого состояния мы можем перейти в 26 различных состояний (на самом деле меньше), причем все возможные переходы зависят именно от состояния, а не от самой строки. На изображении — пример перехода: из состояния, которое выделено синем цветом по букве a мы перейдем в состояние, выделенное желтым цветом.

Теперь, подсчитаем для каждого состояния величину (кол-во букв A - кол-во букв B) в строке, начиная с этого состояния. Если в данный момент ходит первый игрок (на четной диагонали), то это значение надо максимизировать, если второй (на нечетной диагонали) — минимизировать. Реализовать это несложно в виде рекурсии с мемоизацией.
Победителя можно определить по значению состояния, соответствующему клетке (1, 1).
Асимптотика: O(2n × (n + alpha)), где alpha — размер алфавита.
354C - Вася и красивые массивы
В задаче было необходимо найти максимальное d, такое, что ai ≥ d, ai mod d ≤ k.
Пусть m = min(ai), из условия следует, что d ≤ m. Рассмотрим два случая:
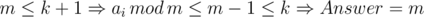
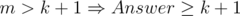 . В данном случае переберем ответ от k + 1 до m, проверить, подходит ли число d в качестве ответа можно следующим образом:
. В данном случае переберем ответ от k + 1 до m, проверить, подходит ли число d в качестве ответа можно следующим образом:
Нам необходимо проверить, что ai mod d ≤ k при фиксированном d, что равносильно 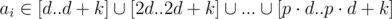 , где
, где 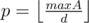 . Так как все упомянутые интервалы [x·d..x·d + k] не пересекаются, то достаточно проверить, что
. Так как все упомянутые интервалы [x·d..x·d + k] не пересекаются, то достаточно проверить, что 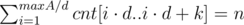 , где cnt[l..r] — количество чисел ai в интервале [l..r].
, где cnt[l..r] — количество чисел ai в интервале [l..r].
Итоговая асимптотика решения: O(maxA log maxA), доказательство основывается на сумме гармонического ряда.
Данная задача решается динамическим программированием. Рассмотрим для начала решение за O(n3).
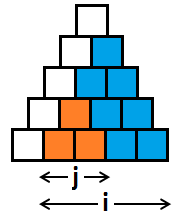
Пусть dp[i][j] — ответ для выделенной синим цветом на изображении части (минимальная стоимость передачи всех ячеек, которые находятся в синей области). Тогда в dp[n][0] будет содержатся ответ на задачу.
Как пересчитывать такую динамику? Понятно, что в самом левом столбце (внутри синей части) мы выберем в качестве вершины подпирамиды максимум одну ячейку. Если мы выберем две, то одна из данных подпирамид будет полностью содержать другую внутри (как синяя подпирамида содержит оранжевую). Теперь, переберем за O(n) ту клеточку, которая будет вершиной подпирамиды и получим следующий переход:
Для упрощения формул будем считать, что 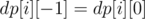 .
.
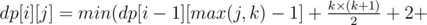
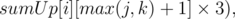 0 ≤ k ≤ i, где k — высота, на которой мы выберем вершину или 0, если в данном столбце не будет выбрана подпирамида, а sumUp[i][p] — количество помеченных клеточек в i-том столбце, на высоте начиная с p, их нам придется передавать по одной операциями первого типа.
0 ≤ k ≤ i, где k — высота, на которой мы выберем вершину или 0, если в данном столбце не будет выбрана подпирамида, а sumUp[i][p] — количество помеченных клеточек в i-том столбце, на высоте начиная с p, их нам придется передавать по одной операциями первого типа.
Можно сократить одну степень, пересчитывая динамику так:
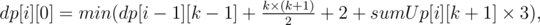 0 ≤ k ≤ i;
0 ≤ k ≤ i;
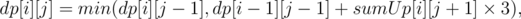 для всех j > 0.
для всех j > 0.
Доказательство того, что это корректно довольно просто и оставляется читателю. :)
Также можно заметить, что нам не выгодно брать подпирамиду с высотой больше, чем 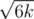 , так как за нее мы заплатим > 3k, однако, если передавать все клеточки по одной мы заплатим всего 3k. Таким образом второе измерение (j) в динамике можно сократить до
, так как за нее мы заплатим > 3k, однако, если передавать все клеточки по одной мы заплатим всего 3k. Таким образом второе измерение (j) в динамике можно сократить до 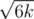 .
.
Также, чтобы получить АС необходимо хранить только два последних слоя динамики, иначе не хватит памяти.
Асимптотика решения: 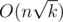 .
.
354E - Счастливое представление числа
Авторское решение, намного сложнее предложенного участниками во время контеста:
Для начала напишем ДП за O(N * lucky_count(N)), где lucky_count(N) — количество счастливых чисел до N, lucky_count(10n) = 3n. Видно, что для всех достаточно больших N решение существует. На самом деле для всех N > 523.
Теперь, скажем для чисел ≤ 10000 у нас есть решение, найденное ДПой. Решим задачу для больших чисел:
Следующая и ключевая идея — разделить задачу на две части. N = N1 + N2. Выберем N1 и N2 так, чтобы для них можно было легко найти ответ, а также, найдя 2 решения, было возможно их объеденить в одно. Пусть N1 = N mod 4000, N2 = N - N1. Однако, тут может появиться проблемма с тем, что для N1 нет решения, тогда сделаем N1 = N1 + 4000, N2 = N2 - 4000.
Теперь решение гарантированно существует и для N1 и для N2, причем в решении для числа N1 мы будем использовать только числа из не более, чем 3 цифр ( < 1000). Доказательство довольно просто: если N1 < 4000 — то очевидно; иначе — если в решении используется число вида (4000 + some_lucky_number), то заменим его на просто some_lucky_number и получим решение для (N1 - 4000), однако его не существует!
Решение для N1 мы нашли при помощи ДП, теперь нам нужно найти решение для N2. Если оно будет использовать только числа вида (some_lucky_number × 1000), то мы сможем легко объеденить его с решением для N1, по-этому будем искать именно такое решение. Тут мы будем использовать тот факт, что N2 делится на 4. Для простоты поделим N2 на 1000, а в конце просто умножим все Ans2(i) на ту же 1000. Пусть P = N2 / 4. Теперь будем конструктивно строить решение. Рассмотрим, к пример, P = 95: идем по цифрам этого числа, последняя цифра — 5, означает, что мы хотим в пяти числах ответа на последнюю позицию (в десятичной записи) поставить цифру 4, хорошо — ставим и в последнем, шестом, числе оставляем на последней позиции 0. Идем дальше, цифра 9 — у нас нету девяти чисел, но мы можем семь четверок заменить на четыре семерки, тогда нам на вторые позиции надо поставить (9 - 7) четверок и 4 семерки, в сумме в 6 чисел, как раз то, что надо.
Таким образом, если очередная цифра d ≤ 6, то просто в первые d чисел ответа ставим цифру 4 на очередную позицию, если же d > 6, то в 4 числа ставим цифру 7 и в d - 7 чисел ставим цифру 4. Во всех остальных числах оставляем на данной позиции 0.
Если Ans1(i) — ответ для числа N1, Ans2(i) — для числа N2, то ответом для числа N будет просто Ans(i) = Ans1(i) + Ans2(i).
Асимптотика решения на одно число: O(logN).
Во время контеста многие участники сдали следующее решение:
dp[i][j] — можем ли мы расставив цифры на последние i позиций чисел ответа так, чтобы получить верные последние i цифр в сумме и перенос на следующий разряд был равен j. Тогда решение существует, если dp[19][0] = true, чтобы восстановить ответ просто для каждого состояния запоминаем, из какого состояния мы в него пришли. База — dp[0][0] = true. Переход — перебераем, сколько мы поставим четверок и сколько семерок в i-тый разряд.











Вот это я понимаю, человек основательно подошёл к подготовке контеста. Разбор создан за 2 месяца (!) до самого контеста. А кто-то и через неделю после раунда разродиться не может.
Я надеюсь, большинство все-таки понимает, что 2 месяца назад был создан просто черновик поста без самого разбора. В общем-то, тогда еще и задач большинства не было :)
Вопрос по Ediv2. Судя по асимптотике, в авторском решении проверка на то, что каждый a[i] входит в один из отрезков, занимает log(maxA). Можете поподробнее описать, как этого добиться.
Мне тоже интересно, как получается такая асимптотика.А, я понял. Итак, значение cnt считается за константное время с линейной предобработкой: посчитаем, сколько всего ai = j для каждого j, а потом вычислим частичные суммыПроверка числа d (как ответ) будет осуществлена за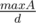 операций. Проверка всех d от 1 до maxA будет работать за O(maxA log maxA), так как:
операций. Проверка всех d от 1 до maxA будет работать за O(maxA log maxA), так как:
Спасибо большое за объеяснение
Такой вопрос. На контесте по С позаходили решения с асимптотикой типа O(a log a log n). Например, моё имеет сложность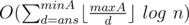 , что на тесте превращается в
, что на тесте превращается в 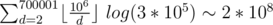 . И это не какие-то там сложения, а скачки по памяти в бинпоиске, вроде много. Тем не менее, в запуске на этом тесте решение отрабатывает 249 мс. Почему не тлешится? Или не много?
. И это не какие-то там сложения, а скачки по памяти в бинпоиске, вроде много. Тем не менее, в запуске на этом тесте решение отрабатывает 249 мс. Почему не тлешится? Или не много?
UPD: ну ок, там ещё брейки, но конкретно на этом тесте
upper_boundвызывается почти 9 * 106 раз, что почти 2 * 108 скачков по памяти.GOOD!
You can use Google to translate it into English.
I will try to translate it today.
Еще решение по Е (более простое, как мне кажется):
Посчитаем все числа d[i], равные x*4 + y*7, где (0 <= x + y <= 6). Таким образом мы уходим от задачи для шести чисел в ответе и можем считать ответ как для одного числа, но вместо 0, 4 и 7 мы будем использовать d[i] (28 чисел).
Запустим рекурсию по одному параметру n — число, для которого нужно найти ответ. Понятно, что если n == 0, то ответ true, иначе переберем d[i] и найдем такие i, что (n — d[i]) % 10 == 0. Тогда запишем d[i] в ответ и запустим рекурсию для числа (n — d[i]) / 10.
Сложность — O(3^log10(n)), но на самом деле нам придется перебирать все варианты только в том случае, когда ответ отрицательный, т.е. на маленьких тестах.
Подскажите пожалуйста, как именно нужно решать задачу D из div2. Не понимаю я свою ошибку на 4 тесте.
Если что-то не понятно из разбора — пожалуйста, уточните что именно.
На счет Вашего решения. Рассмотрим тест:
Хорошие строки: c, cc, cca, ccc, ccac, cccb, cccc, ccacc, cccbc, ccccc.
Ход игры: c -> cc -> cca -> ccac -> ccacc. Ответ — FIRST, у Вас — SECOND.
Тоесть надо рассматривать именно сами возвожные наборы хороших строк. И не верно представлять, что игроки играют на поле? Они лишь выбирают из хороших строчек оптимальный вариант?
Да, именно так. Поле нужно только для того, чтобы дать определение хорошим строчкам.
Альтернативное решение задачи С.
Отсортируем все числа по возрастанию. Будем сдвигать окно размера К, и для каждого окна для каждого из чисел Х от 1 до maxA будем хранить, сколько раз числа из окна делятся на Х. Для сдвига окна просто считаем для числа, которое входит/выходит из промежутка все делители, и прибавляем / вычитаем единицы для всех делителей. При этом работаем только с теми делителями, которых не занулились ранее — если на каком-то интервале, заканчивающемся в одном из наших чисел определенного делителя стало 0, то соответствующее число нельзя уменьшить так, чтобы оно делилось на этот делитель, значт больше его не трогаем. Самый большой делитель, который остался после прохождения окном максимального числа и есть ответ.
Ассимптотика —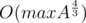 , если использовать стандартную оценку на количество делителей числа,кубический корень, и генерить все делители за время, пропорциональное их количеству. На шустрых серверах кодфорсеса заходит за 0.4
, если использовать стандартную оценку на количество делителей числа,кубический корень, и генерить все делители за время, пропорциональное их количеству. На шустрых серверах кодфорсеса заходит за 0.4
Суммарное количество всех делителей всех чисел от единицы до n —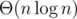 , как я недавно узнал из Википедии. Получается
, как я недавно узнал из Википедии. Получается 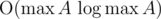 . Да это же такая же асимптотика, как у авторского решения!
. Да это же такая же асимптотика, как у авторского решения!
Если что, эта оценка ничего сверхъестественного из себя не представляет. Чисел, делителем которых является 1 —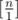 , чисел с делителем 2 —
, чисел с делителем 2 — 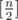 , с делителем 3 —
, с делителем 3 — 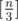 и так далее. Значит суммарное количество делителей всех чисел до n —
и так далее. Значит суммарное количество делителей всех чисел до n — 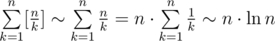 .
.
UPD. Ура, похоже поменялся движок отображения формул, теперь формулы выключные, а значит верхние и нижние ограничения в больших символах отображаются как надо!
Э? Видимо, в последние два дня успели поменять. Когда я писал комментарий сверху (про авторское решение), мне ещё приходилось добавлять \limits. Actually, let’s test this:
Не, у меня всё так же, как раньше. И в твоём сообщении больше всего похоже на \limits:
\sum\limits_{k=1}^n.А про формулу — да, я сам потом понял, но объяснение и общественно полезно, спасибо. Можно даже конструктивно: за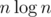 считает все делители всех чисел (даже в отсортированном порядке) цикл
считает все делители всех чисел (даже в отсортированном порядке) цикл
Раньше
\limitsто ли не давал никакого эффекта, то ли вообще не собирался. То есть я явственно помню что раньше нельзя было добиться нормального отображения именно сверху и снизу.Not able to understand anything related to "354B — Game with Strings". Can anyone provide a simpler explanation and a reference solution?
Can someone please explain the question Vasya and Beautiful Arrays ????
Разбор задачи D я понял только после того, как сдал ее :)
Can someone please explain Problem C : Vasya and Beautiful Arrays again?
My thoughts is like this:
Let m be the minimum numeber in A, which is the maximum possible ans
so if m <= k+1, m is the answer
for m > k+1, we have to brute force answer from k+1 to m,
for easy understanding actually we can brute force from 1 to m
Let d be the current testing answer, 1<=d<=m
For a specific d, we have to check if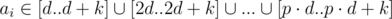 where
where 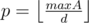 It can be achieve by something like partial sum, using O(p) = O(maxA / d)
It can be achieve by something like partial sum, using O(p) = O(maxA / d)
so in total it's O(maxA/1 + maxA/2 + ... + maxA/m)
= O(maxA * (1+1/2+...+1/maxA)) //m can be as large as maxA
= O(maxA * ln(MaxA)) //from wiki, partial sum of harmonic series
Hi. Would you please help me to clarify why k+1 is chosen?
Why k+1 is the boundary compared to m?
Thanks
I think we can think this way:
1. m = min (A) is the maximum possible answer we can get
2. x is a possible solution iff a_i % x <= k for all i
3. For any positive number c, c% (k+1) <= k
if m <= k+1, for any positive number c, c%m <= k (by 3)
a_i % m <= k for all i (by 2)
m is a possible solution, also the maximum one (by 1)
А почему не получится сдать задачу D (div 2) "черепашкой"?
Вроде бы интуитивно понял, почему. Но вот как это доказать по-строже, не понимаю. Может быть кто подскажет?
Если бы Вы объяснили, что значит "черепашкой" — то может и подскажет :)
Окей. Давайте введем функцию f(i, j), которая нам будет отвечать на вопрос: кто выигрывает в клетке [i, j]. Если f(i, j) > 0 => выигрывает первый, если < 0, то -- второй. В таком случае, f(i, j) += min( [i, j — 1], [i — 1, j]) или f(i, j) += max( [i, j — 1], [i — 1, j]), в зависимости от того, какой игрок сейчас ходит. Понятно, что max будет iff сейчас ходит второй игрок, а min iff сейчас ходит первый игрок.
а, ок. Посмотрите разбор теста тут. На этом тесте Ваше решение упадет, так как не учитывает, что одну строку можно получить несколькими способами. Строку
ccможно получит в клетках (2, 1) и (1, 2).Да, я посмотрел уже.
Возникла такая такая мысль.
Вы мыслили при разборе строками, а если мыслить при разборе, как говорю я, а затем пройтись еще 2 раза по таблице, считая следующее:
Будем смотреть, могли ли мы попасть в ячейку [i, j + 1] ([i + 1, j]) или нет. Делать это будет следующим макаром: Находясь в ячейке [i, j], братюня будет решать, хотел бы он сходить в ячейку [i, j + 1] ([i + 1, j]), либо нет (т.е. выиграет ли он там, али нет). Если хотел бы, то пусть пойдет в ту или (и) в другую. Если ни в какую бы не хотел, то ему все равно придется сделать выбор, поэтому пускай идет в обе ячейки. Тогда, после таких махинаций, у нас появятся недоступные и доступные клетки. Давайте пересчитаем динамику, которую мы считали в начале еще раз, только с учетом недоступных клеток.
В таком случае, все равно не получится?
Не должно, так как одной строке может соответствовать много различных путей и более, чем две клетки. То есть нам не хватит рассмотреть только варианты (i + 1, j) и (i, j + 1).
How do we implement summation(i=K+1,i=max A/d)cnt(i*d,i*d+k)=n in 354C??
We can precalculate partial sums:
cnt[i] = count of numbers ≤ i we have in array a.Now, this summation can be implemented just like this:
I think, this solution 4770602 is quite clear to understand it.
For "Game with strings": Can someone explain to me why "5 cbbbb bcbbb aacbb aaacb aaaac " gives the first player as the winner? He has to start on 'c' and then is dragged by the second player on the right side of the main diagonal. The best player 1 can obtain is "cbcbcbcbc" which is a clear defeat for him.
After first 2 moves the string will be "cb" (the only good string of length 2). Then the first player can extend it to "cba". "cba" is a good string, because of path [(1, 1), (2, 1), (3, 1)]. Now, first player can always write letter "a" and obtain string "cbaaaaaac" in the end. So, the answer is FIRST.
One move in this game is just writing one letter to the end of string, but not moving to some cell. These two games are not equivalent!
i have a question about d problem.
5 cbbbb bcbbb aacbb aaacb aaaac
in this input. the jury's answer is "first". but i think the answer should be "second". i will explain it;
note that the player are playing optimally.
1.step — the first player chooses (1,1) cell that is only option. (a = 0, b = 0) 2.step — the second player chooses (1,2) because if he goes down he will lose.(a = 0, b = 1) 3.step — the first player chooses (2,2) because if he goes right it is obvious that he will already lose.(a = 0, b = 1) 4.step — the second player chooses (2,3).(a = 0, b = 2) 5.step — the first player chooses (3,3).(a = 0, b = 2) 6.step — the second player chooses (3,4).(a = 0, b = 3) 7.step — the first player chooses (4,4).(a = 0, b = 3) 8.step — the second player chooses (4,5).(a = 0, b = 4) 9.step — the first player chooses (5,5).(a = 0, b = 4)
so the second player wins.
can any one explain that why answer is "first" ?
can anyone explain please ?
The comment just above yours asks exactly the same question and has an answer.
In A, if we have been asked to find the number of solutions which has digits k and sum d. Then can we find the solution or not? If yes, then what are the solutions and their time complexity? Please someone help on this.