wonderful_trip's blog

Questions about updating Two Dimensional Binary Indexed Tree (2D BIT)?
By wonderful_trip, history, 4 years ago, In English

When learning about 2D BIT, I have the question that 2D BIT can be easily updated 1 element and get sum, but can update the range ?

Problem:

for each query, you need to update the rectangle (x, y, u, v) each coordinate of a rectangle with upper left corner (x, y) and lower right corner being (u, v) incremented by c "at the same time".

After the update, we can find the sum query (x1,y1,x2,y2);

For example:

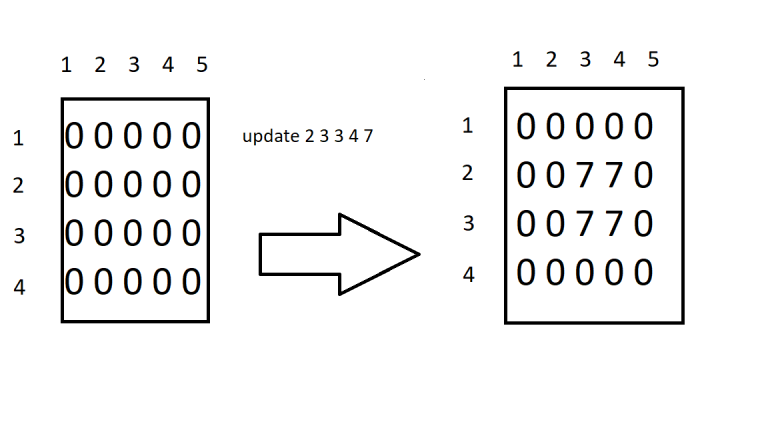
Sum(2,3,3,4) is 28;

Is it possible to solve this problem? If so, please show how to do it!!!

thanks for help!!!

  • Vote: I like it
  • +7
  • Vote: I do not like it

»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by wonderful_trip (previous revision, new revision, compare).

→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it -17 Vote: I do not like it

You can literally google up 2D bit and the first result shows exactly what you described.

Edit: I understand that I am wrong since I did not read the post properly. I deserved all the downvotes. In my defense tho, you can search up 2D BIT range sum range updates which also gives the results about the same topic.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Comments on

    https://www.geeksforgeeks.org/two-dimensional-binary-indexed-tree-or-fenwick-tree/

    is sum (x, y, u, v)

    But it just tells us how to update an coordinates one by one.

    What I want is to update the all coordinates of a rectangle (x, y, u, v) of a rectangle with the top left corner (x, y) and the lower right corner being (u, v ) increment c at "the same time".

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
      ← Rev. 3   Vote: I like it -9 Vote: I do not like it

      So I'm assuming you are not familiar with 2D prefix sum. Let's again explain why the formula for getting the sum works. Let our subrectangle have the lower-left corner $$$(x_1, y_1)$$$ and the upper-right corner $$$(x_2, y_2)$$$. So for getting the sum, first we get the sum from origin to $$$(x_2, y_2)$$$, but then all number having $$$x$$$ less than $$$x_1$$$ or $$$y$$$ less than $$$y_1$$$ should not be counted, so then we subtract the sum from the origin to $$$(x_1 - 1, y_2)$$$, and then from the origin to $$$(x_2, y_1 - 1)$$$. But then all the number having $$$x < x_1$$$ and $$$y < y_1$$$ is now subtracted twice, while we only need them to be subtracted once, so we now add the sum from the origin to $$$(x_1 - 1, y_1 - 1)$$$.

      The trick is the same for the updating operation. First, we need to update from the origin to $$$(x_2, y_2)$$$ with the value $$$c$$$. Now we update all numbers from the origin to $$$(x_1 - 1, y_2)$$$ with the value $$$-c$$$, as well as all the numbers from the origin to $$$(x_2, y_1 - 1)$$$. And then finally we add the number from the origin to $$$(x_1 - 1, y_1 - 1)$$$ with $$$c$$$ again.

      Edit: the way I describe here is "range update" with "point query", so apparently is not the thing that you wanted.

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry, the question I was going to ask was not like that but I asked the question unknown.

        I understand the 2D prefix total. But I mean that after the update, when finding the sum in the above example in cell 3 4 will be 28, not equal to 7 as your way.

        Because what I want to ask is an update to find the totals query, not the point query.

        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
          ← Rev. 2   Vote: I like it -10 Vote: I do not like it

          Ok so, sorry for misunderstanding your problem. Until now I don't think there is an effective way to do that with BIT. I mean, does 1D BIT even have that kind of updating operation? If you want range-update with range-query in the 1D problem you probably end-up using segment tree with lazy-propagation.

          For the 2D problem, the lazy-propagation segment tree is even harder to implement (and I don't know if it possible tho, since I also tried once and failed).

          If you want alternatives, I think you should try to do things like, offline processing.

          → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by wonderful_trip (previous revision, new revision, compare).

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by wonderful_trip (previous revision, new revision, compare).

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by wonderful_trip (previous revision, new revision, compare).

→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it +24 Vote: I do not like it

This article describes how to do range update and sum query for $$$d$$$-dimensional BIT in $$$\mathcal{O}(4^d \log^d{n})$$$.

TLDR:

If you let $$$a_{i, j}$$$ to be the amount that was added to suffix rectangle of $$$(i, j)$$$, then the value at point $$$(x, y)$$$ is $$$A_{x, y} = \sum \limits_{i \le x, j \le y} a_{i, j}$$$.

Now, the prefix sum of $$$A$$$ can be expressed as:

\begin{equation} \sum \limits_{i \le x, j \le y} A_{i, j} = \sum \limits_{i \le x, j \le y} \sum \limits_{i_1 \le i, j_1 \le j} a_{i_1, j_1} = \sum \limits_{i \le x, j \le y} a_{i, j} (x-i + 1) (y-j + 1) \end{equation} The last equation is achieved by considering the contribution of each $$$a_{i, j}$$$ to the answer.

When you expand the brackets you get expressions like prefix sum of $$$a$$$, multiplied by some subset of indices, and by some constant. This values can be calculated, storing BIT for every subset of indices (e.g. $$$a_{i, j} \cdot i$$$). For range update and range sum you simply decompose every rectangle into prefix/suffix rectangles.

→ Reply