Сортировка массива за O(n)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Всем привет.
Когда-то давно я писал как много пользы может принести бор, если его использовать не по его назначению. ссылка
Одним словом, если написать сортировку подсчетом, и вместо обычного массива для подсчета использовать бор как ассоциативный массив, то можно добиться асимптотики O(n) с не очень большой константой. Т.е. просто закинуть все числа в бор и после этого дфс-ом пройтись по состояниях (тем самым просто выводить числа в лексикографическом порядке).
Но придется пожертвовать памятью, т.к. каждая вершина бора будет содержать ссылки не следующие вершины для каждой цифры.
P.S. Для корректной работы все числа надо дополнить лидирующими нолями.
UPD. код
Но мне интересно есть ли задачи где удобнее использовать этот алгоритм вместо квик сорта и/или других сортировок за O(n * log(n)).

Комментарии (9)

Написать комментарий?

Helgui

11 лет назад, # |

← Rev. 2 →

На самом деле алгоритм псевдолинейный, т.к. добавление числа X в бор происходит за O(log(X)). Но применительно к олимпиадным задачам, согласен, можно считать его линейным.

→ Ответить

yermak0v

11 лет назад, # ^ |

-6

Разве что за log_10(x).
Из-за дополнения лидирующими нулями добавление можно считать константой. Т.е. если числа до 10^9 — то за 9 и т.д.

MrDindows

Кстати, если принять 10 за переменную p, то асимптотика по времени и памяти получается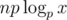 $\text{[math]}$ , ведь в каждой вершине бора вы храните по p указателей. А обзывать число $\text{[math]}$ константой не хорошо как-то)

← Rev. 4 →

Добавление за n * log_p и дфс за n * p. Почему в сумме такая асимптотика? Или я не прав? Теперь понял. P.S. тег <s> работает тут?

При создании вершины вы обнуляете p указателей.

← Rev. 6 →

Такой бор имеет название "цифровой бор".

Асимптотика не O(n), а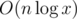 $\text{[math]}$ , ну и константа в вашей реализации однозначно больше чем у обыкновенных сортировок=)

В задачах его использовать можно, но не вместо сортировок, а как онлайновую структуру с запросами на добавление, удаление и тд. Я, например, использовал его один раз для задачи, в которой надо было при добавлении числа в множество определять его позицию в нём, то-есть количество чисел меньших его. Ну и конечно же, если использовать такой бор, то для битовых записей чисел, а не десятичных , операции деления нам ни к чему)

Upd. Ещё стоит отметить, что неявное дерево отрезков для чисел [0, 2^k - 1], есть ни что иное, как цифровой бор глубины k.

Вот тут ещё его модификация описана и некоторые возможности: Сверхбыстрый цифровой бор

-8

Таки если использовать битовые записи чисел — то будет меньше памяти, но время будет log(x). Т.е. в асимптотической плане не будет круче квик сорта.
А так добавление за длину числа — т.е. за log_10(x), немного быстрее, но памяти тоже больше.
Итого свои плюсы и минусы.

Выше ответил по этому поводу.

Xellos

Well, if we have an array of integers, then fast implementations of quicksort are the right way to go. While regular quicksort has worst case performance of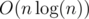 $\text{[math]}$ , its constant is so low that it's hard to beat it in real-time performance.

The trie approach bases on constant number of bits. However, when the sorted numbers are in the range [0, n) (still, that's a very special case), then it's enough to use CountSort; otherwise, we need to remember the numbers as strings of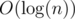 $\text{[math]}$ digits, so building the trie takes 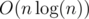$\text{[math]}$ time anyway.

Блог пользователя yermak0v