344A - Магниты
По определению каждый островок состоит из последовательных одинаково направленных домино. Значит, в местах, где соседние домино направлены не одинаково, кончается один островок и начинается следующий. Значит, если таких мест x, то ответ равен x + 1.
Сложность решения O(n). Автор задачи: gen.
Бонус: Задача была придумана в день перед контестом и полностью дополнила физически направленный комплект для DivII :]
344B - Простые молекулы
Первое решение. Во-первых, заметим, что сумма a + b + c должна быть чётной, потому что каждое ребро прибавляет два к сумме. Теперь допустим, что между 1-ым и 2-ым, 2-ым и 3-им, 3-им и 1-ым атомами есть x, y и z связей, соответственно. Поэтому нам нужно решить систему x + z = a, y + x = b, z + y = c. Можно заметить, что решением этого уравнения являются длины касательных на треугольнике со сторонами a, b, c к его вписанной окружности, и равняются 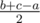 ,
, 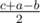 ,
, 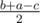 . Если бы в задаче просили проверить только, можно ли построить такую молекулу, то хватало бы проверить нестрогое неравенство треугольника для a, b, c.
. Если бы в задаче просили проверить только, можно ли построить такую молекулу, то хватало бы проверить нестрогое неравенство треугольника для a, b, c.

Второе решение. Переберём значение x. Для него значения y и z определены однозначно: y = b - x, z = a - x.
Сложность решения O(1) / O(n). Авторы задачи: gen, andreyv.
Бонус: Можете ли вы решить задачу для произвольного n? Когда и как можно построить связный граф?
343A - Рациональное сопротивление
Если с помощью k элементов можем получить дроби  , то нетрудно посчитать, что с помощью k + 1 элементов можно получить дроби
, то нетрудно посчитать, что с помощью k + 1 элементов можно получить дроби 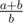 и
и 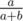 . То есть прибавление одного элемента эквивалентно одному шагу алгоритма Эвклида для числителя и знаменателя в обратном направлении. Значит, ответ равняется количеству шагов стандартного алгоритма Эвклида.
. То есть прибавление одного элемента эквивалентно одному шагу алгоритма Эвклида для числителя и знаменателя в обратном направлении. Значит, ответ равняется количеству шагов стандартного алгоритма Эвклида.
Сложность решения 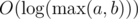 . Авторы задачи: gen, andreyv.
. Авторы задачи: gen, andreyv.
Бонус: Вначале мы думали об общей задаче (можно соединять два любых элемента, как многие неправильно поняли задачу), однако случился момент эврики, и мы поняли, что данная задача неожиданно естественно сводится к НОД. Кстати, дерево результатов – http://en.wikipedia.org/wiki/Calkin%E2%80%93Wilf_tree.
343B - Переменный ток
Вначале решим другую задачу: дана строка, состоящая из символов A и B. Если i-тый символ А, то на i-том шаге верхний провод (на рисунке) кладётся поверх нижнего. Если i-тый символ B, то нижний провод (на рисунке) кладётся поверх верхнего. Заметим, что если символ А стоит рядом с символом B, то эти два заплетания можно распутать и получить ситуацию, которую описывает та же строка, в которой выкинуты эти два символа. Поэтому провода можно распутать тогда и только тогда, если количество А совпадает с количеством В в этой строке. Нашу задачу мы можем свести к вышеописанной следующим образом: на каждой нечётной позиции заменяем – на B, а + на A. На чётных позициях заменяем – на A, а + на B. Можно видеть, что сведение правильное, потому что на каждой чётной позиции – и + всегда стоят перевернутые относительно начала, а на каждой нечётной порядок совпадает с порядком начала.
Сложность решения O(n). Авторы задачи: gen, andreyv.
Бонус: Если тема вас заинтересовала, можете ознакомиться с теорией кос http://en.wikipedia.org/wiki/Braid_theory :] Fun fact: усложнённый вариант задачи был предложен ещё на Round #142, но тогда в решении нашлась ошибка, и задача осталась лежать почти целый год.
343C - Время чтения
Будем искать ответ t двоичным поиском. Рассмотрим конкретное значение t. Рассмотрим первую головку слева h[i], которая может считать p[0]. Если p[0] > h[i], то h[i] просто идёт направо t секунд, и читает все дорожки на пути. Если p[0] ≤ h[i], то у головки есть два выбора:
- идти направо
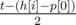 секунд, затем налево
секунд, затем налево 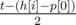 и опять налево ещё h[i] - p[0] секунд;
и опять налево ещё h[i] - p[0] секунд; - идти налево h[i] - p[0] секунд, затем направо h[i] - p[0] и опять направо t - 2·(h[i] - p[0]) секунд.
Естественно, для h[i] выгоднее всего побывать в самой правой точке. Поэтому выбираем по 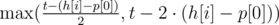 . Дальше двигаем указатель на первую несчитанную дорожку, и повторяем алгоритм для h[i + 1], и.т.д. с каждой головкой.
. Дальше двигаем указатель на первую несчитанную дорожку, и повторяем алгоритм для h[i + 1], и.т.д. с каждой головкой.
Сложность решения 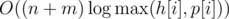 . Авторы задачи: gen, gorbunov.
. Авторы задачи: gen, gorbunov.
Бонус: Задача полностью реальна, если у диска есть только одна головка, и известно, какие данные нужно считать, то оптимальный алгоритм выбирает один из описанных двух вариантов. Это мы слушали на лекции вместе с gorbunov, и от скуки придумали такую задачу ;]
343D - Водяное дерево
Научимся быстро красить целое поддерево. Для этого пронумеруем все вершины в порядке выхода DFS. Тогда каждое поддерево покрывает один непрерывный отрезок номеров вершин. Для каждой вершины запомним границы такого отрезка для поддерева с корнем в этой вершине. Тогда красить поддерево означает покрасить отрезок в дереве отрезков.
Заведём дерево отрезков. Для него выполняется свойство: если вершина v была опустошена, и она до сир пор пуста, то эта вершина покрашена в дереве отрезков. В самом начале «опустошим» все вершины. То есть, покрасим все вершины в дереве отрезков. С помощью этого дерева можно эффективно обрабатывать запросы:
Заполняем вершину v. Стираем всё поддерево v в дереве отрезков. Если до этого поддерево не было пустым, то красим родителя v.
Опустошаем вершину v. Красим вершину v в дереве отрезков.
Отвечаем, заполнена ли вершина v. Если в дереве отрезков сумма поддерева v не равна 0, значит есть такой потомок v, который опустошён сейчас, поэтому вершина v не заполнена.
Идейно похожее, но более простое решение в написании предложил Shtrix.
Сложность решения 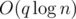 . Автор задачи: gen.
. Автор задачи: gen.
Бонус: Некоторые участники могли заметить схожесть задачи с задачей Ball Machine из BOI 2013, однако решения этих задач имеют мало похожего.
343E - Насосные станции
В этой задаче нужно было найти такую перестановку вершин графа, что сумма максимальных потоков, пропущенных через каждую пару соседних вершин в перестановке, максимальна.
Задача решается с помощью структуры данных дерево Гомори-Ху. Для данного взвешенного графа дерево обладает свойствами:
- Множество вершин дерева совпадает с множеством вершин графа.
- Максимальный поток в дереве между вершинами u и v равен максимальному потоку в графе между вершинами u и v.
Такое дерево на удивление существует для любого взвешенного графа и строится за время O(n·maxFlow). Оказывается, что для данной задачи ответом является сумма весов рёбер в таком дереве.
Докажем это утверждение индукцией по количеству вершин в дереве. Найдём ребро (u, v) с минимальным весом в дереве. Допустим, что для оптимальной перестановки вершин через это ребро проходит больше, чем один путь между парами соседних вершин в перестановке. Сотрём все такие пути, тогда в поддеревьях u и v остаётся в каждом по множеству несоединённых цепочек путей. Соединим все пути в каждом множестве в одну цепочку и получим две цепочки. Эти цепочки соединим одним путём s, который идёт через ребро (u, v). Получили перестановку, которая не хуже оптимальной. Для пути s ребро (u, v) является наименьшим, значит поток по этому пути равен весу этого ребра. Из индукции следует, что в поддеревьях u и v ответ равняется сумме ребёр. Добавляя к сумме вес ребра (u, v), получаем желаемое.
Из предыдущего абзаца ясно также, как строить такую перестановку: Берём наименьшее ребро, для поддеревьев вершин рекурсивно строим цепочки и соединяем их в одну. Так как вершин мало, эту часть можно делать даже за O(n2).
Сложность решения O(n·maxFlow). Авторы задачи: gen, Gerald.
Бонус: Ближе к соревнованию мы решили сделать ограничения лояльней, поэтому прошли также решения, которые O(n2) раз вызывают поток и затем строят дерево Гомори-Ху. Надеемся, этот факт никого особенно не огорчил. (;











По решению 343B: разве ваше решение подразумевает входную последовательность типа "---"?
Конечно, ответ
No. В самом низу задачи есть похожая картинка. ;]Я тоже не совсем понимаю, что у вас написано в решении. В том смысле что ---++--- должен быть BBBAABBB, теперь мы что делаем выкидываем стоящие рядом BB и АА тогда получаем BB за одну итерацию (про несколько итераций ничего не сказано) и должен быть ответ No по вашему признаку, Хотя я такой провод распутаю
Или мы убираем AB и BA тогда получаем BBBB что тоже по вашему признаку должно давать No.
Имеется ввиду: "Запишем другую строку, где i-тый элемент будет A, если на i-том шаге сверху [на узле] был положен верхний провод [верхний в плане вертикального расположения на картинке], и B, если сверху [на узле] был положен нижний провод [нижний в плане вертикального расположения на картинке]".
По примеру в условии задачи, например, получим BBAA.
Вот графическое пояснение: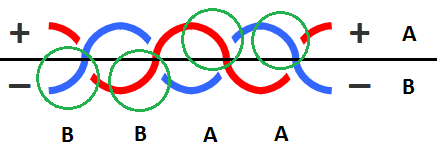
Спасибо.
Мы написали решение подробнее, надеюсь, стало понятнее.
Спасибо, стало понятнее.
Думаю, автор имеет в виду, что подряд идущие одинаковые символы будут выкидываться сразу после того, как они появятся. Так, на 2 шаге будет откинуто ВВ, на 5 шаге будет выкинуто AA, а на 6 и 8 оставшиеся BB.
Ну так да. Это фактически задачка о парных скобках в таком описании, но там то было "напишем строку", я и подумал, что чего то не понял и можно (UPD: таки можно) это как то "параллельно" решить для всего массива сразу, каким то магическим преобразованием
Нет, авторское решение этого не позразумевает. Строка ---++--- будет преобразована в BABBAABA, и ответ да, так как количество A = B.
А я задачу B решал с помощью стека. Бежал циклом слева направо и если стек пуст или последний символ не равен текущему, то добавлял его в стек, иначе удалял. В конце, если стек пуст, то ответ Yes
Да, пожалуй это было решение, которое написало подавляющее большинство. Авторское решение в стеке не нуждается.
Ну, учитывая что в стеке чередуются плюсы и минусы, можно хранить просто его длину и последний элемент.
Можно было еще так рассуждать: Если представить, что красный провод вытянут, а синий наматывается на него, то становится понятно, что -+ соответствует одному витку синего провода по часовой стрелке, а +- — витку против часовой стрелки. ++ и -- ничего не изменяют. Поэтому остается проверить, что было одинаковое количество витков по и против часовой стрелки.
Не совсем понял разбор B (div1). Вроде можно сделать что-то типа проверки на правильную скобочную последовательность. вот решение 4472544
При решении Div1-A, глядя на формулы, не увидел алгоритм Эвклида. Мне пришло решение основанное на эквивалентных преобразованиях электрических цепей. Сначала заметим, что решение всегда существует: для сопротивления a/b мы можем взять схему из a последовательных блоков по b параллельных резисторов. Далее преобразуем схему по правилу Кирхгофа о сумме токов в узлах и жадным образом "группируем квадраты в одиночные резисторы" пока это возможно. Привожу пример для схемы 3/5.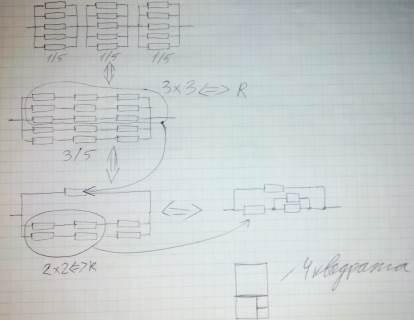
Hai this was my first round in Codeforces. But my code was not accepted and it says that it was wrong with the 3rd test case. What i did was put a loop from 0 to n-1 and i checked ch[i][!=ch[i+1][0] then count++; else continue where 'ch' is the character array(2-D) whose size was Nx3 ...Is this algorithm completely wrong. As i said this was the first round here i did not understand what is wrong with this. If possible please do tell me what is wrong with this algorithm..:(
Please look at link http://codeforces.net/contest/344/submission/4461494.
The log says
Time: 0 ms, memory: 0 KB Verdict: WRONG_ANSWER Input 1 10 Output 0 Answer 1 Checker comment wrong answer 1st numbers differ — expected: '1', found: '0'
I believe this should be self explanatory.
Also it would help playing around with the system before trying to enter a rated match.
Задачу D можно решать без дерева отрезков, с помощью одного сета. Обойдем дерево поиском глубину и запишем вершины в порядке обработки. Итого есть массив длинны N в котором каждое поддерево нашего дерева представляет отрезок. Запомним для каждой вершины v отрезок который является его поддеревом: [L[v], R[v]). Также заметим, что сама вершина находиться на позиции L[v]. Теперь заведем set и добавим в него все номера индексов листков исходного дерева (т.е. такие L[v] где v — листок).
Для того чтобы обработать запрос 1-го типа (заполнить водой вершину v) необходимо удалить из сета все индексы (L[v] <= x < R[v]) и добавить L[predecessor[v]] если predecessor[v] конечно существует. Найдем нужные элементы lower_bound-ом и удалим их за линию — количество удалений не превзойдет количество добавлений и не изменит асимптотику.
Для обработки запроса второго типа (опустошение вершины v) просто добавим L[v] в сет.
Для ответа на запрос третьего типа достаточно установить, что хотя-бы одно число из диапазона [L[v], R[v]) есть в сете — проверка одним lower_bound-ом.
Круто, идейно то же самое, но пишется в сто раз проще!
B div 2 можно также делать жадно — соединяем две вершины, у которых валентность больше всего на данный момент, и уменьшаем эти валентности на 1.
Работает ли такая стратегия, если бы у нас было n вершин? :)
Видимо нет, так как при n=3 две вершины с максимальной степенью обязательно должны быть соединены, что не всегда выполняется для больших n
Ну почему. Если сумма чисел нечетная или максимальное число больше суммы всех остальных, то очевидно, что решения нет. Иначе, если мы уменьшим 2 максимальных числа на 1, то оба этих свойства не нарушатся, так что такое решение верное.
Граф может получиться несвязным, но это легко исправить.
А, я не заметил, что еще связность требуется.
Ну, если n = 3, то связность само собой, поэтому в условии это не акцентировалось.
Небольшая просьба:
может мне кто объяснит, почему решение задачи 343B (переменный ток), которое я отправлял на Delphi Your text to link here... не прошло 38-й тест, а это же самое решение на Free pascal Your text to link here... прошло все тесты? просто интересно в чем причина?
Присоединяюсь к вопросу. Аналогичное решение, аналогичная ситуация с 38 тестом, Delphi и Free Pascal.
Добавление следующей строки после считывания символа
исправляет код на Delphi.
Соответственно, Delphi считывает что-то ещё в этом тесте. Попытаясь вывести эти символы, обнаруживаем 13 и 10 (то есть \r\n). Почему не срабатывает EoLn — надо смотреть тесты (может быть чуть другое окончание строк в этом тесте, например), если же всё выглядит нормально, то я бы списал всё на магию.
Мы с eduardische и Alex_2oo8 подумали и вспомнили, что в Delphi был какой-то баг. Баг вроде бы заключался в том, что переводы строки на некоторых позициях ввода, кратных каким-то степеням двойки, не распознавались правильно.
И в самом деле, 38-й тест содержит ровно 65536 плюсов и минусов, так что перевод строки находится как раз на 65536-й позиции с начала файла, если считать с нуля. Возможно, проблема из-за этого бага Delphi.
Надеюсь, придёт dalex и раскажет подробнее, он вроде писал об этом раньше.
Это Костя писал. Там кажется позиции кратные 80 как-то криво обрабатывались. Сам я не знаю, в чем суть этого бага.
Там Eoln как-то криво работал из-за переполнения буфера. Кажется на кратных 80 дейсвительно.
Спасибо за ответы! Буду знать
Я новичек, кто-нибудь может мне объяснить как алгоритм Евклида относится к задаче про резисторы? Я почитал, это относится к цепным дробям или нет? Подскажите пожалуйста, спасибо.
Алгоритм Эвклида для чисел a и b работает так: пока оба числа больше 0, отнимаем от большего меньшее. То есть из пар (a + b, b) и (a, a + b) получаем (a, b). В задаче же делается такой же шаг для числителя и знаменателя дроби, только в обратном направлении. Поэтому ответ равняется количеству шагов алгоритма Эвклида.
Спасибо, но честно говоря я не понимаю саму нить рассуждений. Зачем нам дается какие элементы мы может получить, используя элемент с сопротивлением a/b? Можете объяснить основную идею решения? Спасибо.
Если у нас есть элемент с сопротивлением , то подключив ещё один резистор последовательно, получаем элемент с сопротивлением
, то подключив ещё один резистор последовательно, получаем элемент с сопротивлением 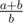 , а подключив ещё один резистор параллельно, получаем элемент с сопротивлением
, а подключив ещё один резистор параллельно, получаем элемент с сопротивлением 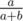 . То есть, по сути мы проделываем один шаг алгоритма Эвклида в обратном направлении. Поэтому количество его шагов для двух данных чисел и равняется ответу задачи (по сути каждым шагом мы отнимаем один резистор от элемента). Заметьте, что условие «минимальное количество» резисторов в задаче является только косметическим, потому что элемент
. То есть, по сути мы проделываем один шаг алгоритма Эвклида в обратном направлении. Поэтому количество его шагов для двух данных чисел и равняется ответу задачи (по сути каждым шагом мы отнимаем один резистор от элемента). Заметьте, что условие «минимальное количество» резисторов в задаче является только косметическим, потому что элемент  можно получить ровно из одного другого элемента.
можно получить ровно из одного другого элемента.
Could somebody please clarify the two choices of head(s) in the solution of 343C-Read Time problem above? I couldn't understand it completely. Thank in advance!
You have to choose one of the two types moving: first to the right or first to the left. You have to use the one which covers more points to the right. Note that both types of moving cover the left point and that's why you have to take as much as points as you can to the right.
Could somebody give me a hint for the bonus at Div2 — B?
Think greedy ;]
will the connections between the atoms be circular? like 1 <-> 2 <-> 3 <-> 4 <-> 5 ... n <-> 1 (again) ?
Can you give a better hint? (Maybe through a spoiler, I suppose)
I think the algorithm that continuously connects the vertex with the smallest degree with the vertex with the largest degree works (here by degree I mean the unconnected edges), and builds a connected graph. I think this can be proved by induction.
Я в задаче Е не строил дерево Гомори-Ху (на самом деле, я о нем услышал после контеста), а написал следующую жадность. В начале найдем поток между каждой парой вершин. После этого выберем 2 вершины, величина потока между которыми максимальная и поставим эти 2 вершины в начало цепочки. Если таких пар несколько, выберем любую. При этом, нам не важно, в каком порядке их ставить в цепочке. Далее будем повторять такое: находим еще не использованную вершину до которой величина потока от последнего элемента цепочки максимальна и ставим ее в конец цепочки. Когда все вершины будут добавлены в цепочку, выведем ее как ответ.
I think there is an issue with Problem 343A — Rational Resistance. Here according to the editorial the answer to the ratio 6/5 would be 6(I have verified this with an accepted solution). But this ratio can be achieved with a resistance of 2 and 3 in parallel, which makes the number of resistors required equal to 5 which would imply the editorial and the system tests to be wrong.
Am I missing something here?
I think it's because the definition of one element only let you add one new unit resistor to another element
Thanks for the nice problems!
I just have a little question on 343C — Read Time. I use the same algorithm and get AC, but my algorithm is running at O(n log^2 n)... as for the step: "Then we move the pointer onto the first unread track" I use another binary search...
how can I implement the same algorithm with O(n log n) as said in editorial?
We hold two pointers: the first points at the first unread track from the left, and the second points at the first unused head so far. So we take this head and read with its help the maximum number of yet unread tracks (note that they are consequent and begin at the first pointer) according to the best of the two choices described in tutorial. Then we move the first pointer to the first yet unread track, and increment the second by one. Thus each pointer moves O(n) times in this iteration of the binary search. Take also in consideration that some heads can be not used at all.
Hi. I was just trying to solve problem A of division 2, but was unsuccessful after hours of effort. I eventually lost patience and decided to see the codes of others. I did understand what was going in the code, but couldn't figure out why this method was chosen in the first place. Can someone please help me understand the solution?
P.S. I'm a newbie with almost no prior knowledge about number theory. :$
The number of islands is always one more than the number of splits between two neighboring dominoes. One can easily convince himself by looking at an image in the description.
There are 4 possibilities of neighboring dominoes:
So, we can deduce that we're only interested in neighboring dominoes that are different. This means we can just count the number of indexes i (1 <= i < N) such that s[i] != s[i+1].
I'm confused by the first sentence of 343A — Rational Resistance tutorial
How can we obtain a/(a+b) with k+1 resistors if obatined a/b wiht k resistors ?
Remember a/a is 1. If we have a/b resistance, put one more resistor parallel will give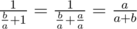
adding one resistor means performing one operation backwards in Euclidean algorithmCan someone explain this ?
gen ?
Suppose you have resistance of(17/3), it could be formed by adding 1 + (14/3). If you have resistance of (3/17), it could be obtained by combining resistance of 1 and 3/14 in parallel.
In terms of variable, a/b could be obtained by 1 + resistors required to create ( a-b)/b resistance, assuming a>b. and a/b if b>a, could be obtained by 1 + resistors required to create ( a/(b-a) ).
Assuming a>b so resistorRequired(a,b) = 1 + resistorRequired(a-b,b).
............
let say r = a-q*b == a%b now at this point, one resistance needs to be connected in parallel to the b/r resistance.
so again problem becomes calculating the requiredResistance(b,r) similar to above problem,
which is similar to the gcd problem.
Hope that helps.
Why it's like gcd(a,b) = gcd(a-b,b) =gcd(a-2b,b) ....
In case of gcd(a,b) = gcd(a-b,b)
Thanks a lot for the nice explanation. Now the use of euclidian algorithm to solve this problem makes sense to me.
Can anyone explain to me the solution for Problem C div2 I understand the transition from
ktok + 1but the part about Euclidean algorithm is beyond mewater tree can be solved by heavy-light decomposition...
Yes, this is almost the most standard problem for HLD. But their solution is cleverer and has lower time complexity. HLD is a little bit overkill for such simple operations.
Nevertheless, HLD can pass the test. My HLD solution passed in 900ms.
Also HLD was a relatively unknown algorithm to the CP community 5 years ago.
Can you explain how to approach this with HLD? I am new to HLD, and not able to get any clue here.
Thanks
I have another O(n) solution for 343B with stack here http://codeforces.net/contest/343/submission/17068970
I wonder why I did wrong in the implementation of lazy propagation for Div1D, could anyone kindly lend some help?
http://codeforces.net/contest/343/submission/20226349
Thanks in advance. =)
Accepted solution for the problem 343A Rational Resistance would give 6 as the output for input a = 10 and b = 7 i.e.10/7. But, if we have 5 ohm and 2 ohm resistors in parallel, then we have the same resistance value 10/7. So minimum value should be 2 resistors for this case. Kindly explain if i am wrong in understanding the problem?
You have only 1-ohm resistors in the beginning. Thus it requires 5 1-ohm resistors to make a 5-ohm resistor, and 2 1-ohm resistors to make a 2-ohm resistor. So according to you answer is 7 and not 2.
In 343D — Water Tree query 1 and 2 can be solved using a dfs to find in time and out time for every node and then using segment tree But what about 3rd query how to solve it??
yeah same question .
Q.343A can anybody explain me why min resistor for 199/200 is 200.....it can be also constructed using 101 resistors(1/2+1/4+1/5+1/40+1/50)
correct!!!
It is because they are separate elements and hence they cannot be added together. Only an element and a 1 unit resistance can be added in series(or parallel)
Thanks
An alternate approach for solving D: Use of lazy segment tree over HLD & Euler path. For every filling, fill Euler path with current query number, and for emptying, fill HLD path from the root with query number. For queries, check which of the seg tree has high query number.
Problem 344A
This is my code, but I don't know how to improve it, so that the time limit won't be a problem anymore. Any help?
You can make two variable for prev and current value and if they are not equal you can increment it.
In Problem C, if more than one of the elements can be in parallel than for ratio 199 and 200 the answer given is 200. But we may solve this in 74. like 1/2+1/4+1/8+1/10+1/50.
Okay it would be like either + denominator to the numerator or + numerator to the denominator.
gen or andreyv or can anyone please explain
Alternating CurrentSolution.Tried so hard but not able to understand it. ATry it using stack