A new season of the interesting COCI contests is kicking off! The first contest is scheduled earlier than usual. It will be on next Saturday(September 28th) and there won't be any contest in October. Let's hope for a high problem quality similarly to previous years. Here's the e-mail sent to the ioi-announce mail list:
Croatian Open Competition in Informatics COCI 2013/2014 Internet online contest series
Over the next seven months we are planning to organize seven online contests as a warm-up for the 2014 season of high school programming competitions. Everyone is welcome to participate!
Each contest will be three hours long and will feature six tasks. The tasks will be of widely varying difficulty; we are hoping to have many beginner or up-and-coming contestants participate, as well as those more experienced.
The first contest will be held on Saturday, 28th September 2013, starting at 14:00 (GMT/UTC). Check out your local times at http://hsin.hr/coci/next_contest.html.
You may use Pascal, C/C++ or Java as your programming language of choice.
The two relevant websites are: http://hsin.hr/coci/ — information about the contest http://evaluator.hsin.hr/ — contest system
We hope that you will join us or encourage your students to do so!
This is the eighth year in a row that we are hosting the COCI series. You can find tasks (statements, test data and solutions) from the previous seven years at http://hsin.hr/coci/. That is over 300 original tasks for students to practice on!
Project Manager











You're not allowed to log in from this location.?What's the name of the contest you're logging in to?
Juniorska hrvatska informaticka olimpijada 2013.
In other words, "Junior Croatian Olympiad in Informatics". That doesn't sound like "Croatian Open Competition in Informatics". In fact, it sounds like something for Croatian students only. Mystery solved...
Damn! It was hard :D
Shit, just needed another 15 — 20 seconds to submit 3rd one for full score :(. What is formula for second problem? Mine gets only 60 points.
Just a rainbow of GCDs and LCMs :D:D
That is mine (full acc):
Due to low constraints it's even easier:
Well, Java solutions are not tested yet, but answer is m — gcd(n, m) I believe
Do you use em dash for minus? : ]
I just use whitespaces where they should be — which codeforces parser sometimes get wrong way
The difficulty estimates were really bad. Problem 5 is easy (divisor testing up to square root, which is a very simple idea gives 80% of full score, which is too much for 5), and 6 is extremely hard, with only 20% of points for either O(NL) or O(NM) (L is sum of lengths), where O(NM) needs KMP — it should be given some more points.
That being said, does anyone have a fullscore idea for problem 6?
First we build suffix array of a big string. For each pattern string we want to know first occurrence in the big string. We find interval in suffix array in which pattern occurs by binary searching suffix array then we find out suffix in that interval that starts in the minimum position. Finding minimum can easily be done with segment tree.
Example:
matching interval is:
We sort pattern strings by position of first occurrence in big string. For each pattern string we want to find out number of positions where none of the letters is matched, where only one letter is matched, first two letters are matched and so on. Of course we are only interested in part of the big string before out first occurrence. Again finding interval in which first k letters of pattern string are matched can be done binary searching suffix array. Now we want to know how many of suffixes in that interval are positioned left of pattern's first occurrence. We can do that with Fenwick tree because we sorted pattern strings by their first occurrence so after we're done with some pattern we need to put 1-s on certain positions in Fenwick tree before we process next pattern
"We find interval in suffix array in which pattern occurs by binary searching suffix array"Can we preform this step in O(log(N)) time?
I did it in O(log^2 n). You need to hash big string and pattern. Then you need log n to find longest common prefix to compare suffix and pattern and log n for binary searching suffix array. You need to do that to find lower bound and upper bound.
You can find lcp O(1) with using RMQ , so You can perform it O(logN).
How LCP can help us to find our interval?
Well , when you are at any step in binary search you have to find "Longest Commom Prefix" of this 2 strings and compare them.
Still don't get it.
So, we have a suffix array of big string and some pattern strings. For each pattern string we want to know the largest interval in suffix array of big string, in which each suffix contains pattern string as prefix. What should we do?
B, and others areS1 , S2 , .. , SnB + '#' + S1 + '#' + S2 + '#' + ... + Sn( + operator is same as c++ '+' operator with strings)Hhuge string andNlenght of huge stringLCP[i] = lcp of H[suffix_array[i],N] and H[suffix_array[i + 1],N]RMQ(l,r) = min LCP[i] , i >= l and i <= rso RMQ(l,r) gives you lcp of
H[suffix_array[l],N]andH[suffix_array[r],N]Hope ,this is clear enough...
Get it, thank you.
Does anyone knows the solution of 4th 100% point solution, is 50% and 100% solutions are connected or too much different?
100% is 50% solution with multiset =) 100%
I believe heap is superior to multiset here :)
Sure, it is. But with time limit as large as this, both solutions pass comfortably (my solution runs 0.5s on the largest testcase), and I'm more used to set/map than heap.
It's just a matter of coding style. I'd use heap if the time limit was tight, though.
Sort the bags by increasing size, the objects by increasing weight.
List all objects that can go to the smallest bag. It's obvious that you want to take the most expensive one (since those objects can't go to any larger bag), if there is one. So you do it.
For the 2nd bag, take all objects except the one you added before, and add to them all that can go to the 2nd bag but not to the 1st. You're in an identical situation as before, so take the most expensive object. And so on for all bags.
It can be implemented with 2 pointers and 1 multiset, in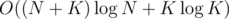 .
.
A possible 50% solution uses dynamic programming (first i elements cover first j bags, how much can it be worth?), or just this idea without sorting and adding objects efficiently. It can be different, but doesn't have to.
well actualy my 50% solution is dp after sorting also.
But you can sort in O(N2 + K2). It doesn't have to be efficient, too. (I didn't mention the sorting with DP because it's just not the center of the idea :D)
Our problem is not sorting O(n log n) or O(n ^ 2) , we both misunderstood each other , whatever no problem , also thanks for sharing solution idea :)
What is the solution for problem C [ Ratar ]? My 8*(n^4)*logn solution got 60%. How to get full points ?
First choose some (i, j) as common corner of the two fields. And then add all sums sum(p, q, i, j) where p ≤ i and q ≤ j to an array (lets say V1) and sort it. Similarly add all sums sum(i + 1, j + 1, p, q) where i + 1 ≤ p and j + 1 ≤ q to an array (lets say V2) and sort it too. Then find how many numbers X(=some number) are in V1 (lets say it is cnt1) and in V2 (let it be cnt2). Then increase answer by cnt1 * cnt2. This can be done in O(V1.length() + V2.length()). Here is how it is done in C++:
Above is the case when one field is in up-left and the other is in down-right of the common corner. Do the same when one field is in up-right and the other is in down-left of the common corner.
Complexity: maximum possible value of V1.length() and V2.length() is N2, so O(2 * N2 * 2(N2 + N2log2N2)) = O(N2 * N2log2N2)
P.S. sum() function is inclusive :)
I have an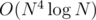 , too, but it runs in 0.88s on the largest test case. If you have an additional log-factor, it's important to take down large constants (like, by looping from i to N, not from 0 to N).
, too, but it runs in 0.88s on the largest test case. If you have an additional log-factor, it's important to take down large constants (like, by looping from i to N, not from 0 to N).
There's a pure O(N ^ 4) solution. Let's fix the left — top corner of one rectangle. Then we need a number of rectangles that upper and left from the fixed corner. So let's iterate in O(N ^ 2) for all possible left top corners of second rectangle and increase a count of certain sums. Then let's iterate over all possible right — bottom corner of first rectangle and add to our answer the count of certain sum. Do this for a left bottom case simmetrically. O(N ^ 4) total. Code.
got it, i have used map to store the rectangle's sum and BIT to get the sum, but it was possible to get rid of them.. thanks.. :)
In ORGANIZATOR we can use sieve eratosthenes and array f[2e6] mean that f[x] is the smallest prive factor of x so we can find all factor of x in O(log x). Next we generate all division of x, it is about log(x)*log(x) number. In contest I only find prive division of x so i fail all test. At the end of contest I see my wrong but too late. Here is my AC solution: http://ideone.com/kmrO5I
Since the maximum number is 2000000, just iterating all possible factors will get AC in very short time.
http://ideone.com/pzdlwJ
Genius!
Results