Обозначим сумму чисел на верхних половинках костей за s1, а сумму на нижних — s2. Если изначально s1 и s2 четные, то ответ, очевидно, 0. Заметим, что если числа на обеих половинках кости одинаковой четности, то при повороте этой кости четность s1 и s2 не меняется. Если же четность чисел на половинках разная, то при повороте кости меняется четность как у s1 так и у s2. Из этого следует, что если s1 и s2 имеют разную четность, то ответ - 1. Если же s1 и s2 нечетные, то нужно проверить, имеется ли в наборе кость с числами разной четности на половинках. Если имеется, то ответ 1, иначе ответ - 1.
Для краткости будем говорить, что в кучки раскладываются числа, нарисованные на кубиках, а не сами кубики.
Заметим, что ответ на задачу, это произведение количеств различных чисел в каждой из кучек. Предположим, что все заданные числа различны. В этом случае ответ равен n2. Предположим теперь, что есть два одинаковых числа, а все остальные различны. Тогда, если мы их положим в разные кучки, то ответ будет равен n2, а если в одну, то n·(n - 1). Очевидно, первый вариант даст большее произведение.
Рассуждая аналогичным образом, можно прийти к выводу, что нужно действовать следующим образом. Возьмем числа, которые встречаются больше одного раза, и закидаем по одному из них в разные кучки, остальные пока отложим в сторону. После этого числа, которые встречаются по одному разу раскидаем поровну в разные кучки. Затем, все числа, которые мы отложили в сторону раскидаем по кучкам произвольным образом.
Рассмотрим старший бит числа m. Если он равен нулю, то во всех 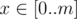 в n - 1-ой позиции будет стоять 0, а значит an - 1 никак не повлияет на ответ и мы можем выбросить его из набора и считать ответ для массива из n - 1 элемента.
в n - 1-ой позиции будет стоять 0, а значит an - 1 никак не повлияет на ответ и мы можем выбросить его из набора и считать ответ для массива из n - 1 элемента.
Если же старший бит числа m равен 1, то an - 1 для некоторых x будет входить в f(x), а для некоторых — нет. Рассмотрим все x, при которых an - 1 не будет входить в f(x). Это, очевидно, 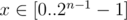 . Среди таких x максимальное f(x), очевидно, будет достигаться при x = 2n - 1 - 1. Попробуем улучшить ответ этим значением.
. Среди таких x максимальное f(x), очевидно, будет достигаться при x = 2n - 1 - 1. Попробуем улучшить ответ этим значением.
Теперь нам осталось рассмотреть 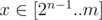 , среди них найти максимальное f(x) и попробовать улучшить ответ этим значением. Заметим, что во всех таких x на (n - 1)-ой позиции находится 1, поэтому мы можем найти максимальное значение f(y) среди всех
, среди них найти максимальное f(x) и попробовать улучшить ответ этим значением. Заметим, что во всех таких x на (n - 1)-ой позиции находится 1, поэтому мы можем найти максимальное значение f(y) среди всех 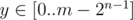 и прибавить к нему an - 1.
и прибавить к нему an - 1.
Заметим, что если несколько девочек стоит в самом начале очереди, то они никогда не будут двигаться, поэтому удалим их, и будем считать, что очередь начинается с мальчика. Также заметим, что относительный порядок девочек при движении не меняется. Посчитаем для каждой девочки момент времени ti, начиная с которого она перестанет двигаться в очереди навсегда. Заметим, что для i-ой по порядку девочки ti ≥ ti - 1. Будем считать ti в порядке слева направо. Посмотрим на какой позиции yi в очереди будет находиться девочка, когда она закончит свое движение, и на какой позиции xi она находится сейчас. Тогда этой девочке потребуется не менее xi - yi времени, чтобы добраться до своего места. Тогда если xi - yi > ti - 1, то ti = xi - yi. Рассмотрим, что произойдет при xi - yi ≤ ti. В момент времени ti - 1 (i - 1)-ая девочка будет находиться на позиции yi, поэтому ti ≥ ti - 1 + 1. С другой стороны, рассмотрим последний момент времени p, когда i-ая девочка стоит непосредственно за (i - 1), но еще не на позиции yi. После этого, в момент времени p + 1 (i - 1)-ая девочка меняется местами со стоящим перед ней мальчиком, а i-ая девочка остается на своей позиции. Затем с момента времени p + 2 до ti - 1 обе девочки меняются местами с впереди стоящими мальчиками. А в момент времени ti - 1 + 1 i-ая девочка наконец встает на свое конечное место. Отсюда следует, что в этом случае ti = ti - 1 + 1.
Разобьем имеющийся граф на цепи. Цепью назовем максимальную по включению последовательность одинаково направленных ребер. Если в каждой такой цепи не менее 2 ребер, то ответ — это количество таких цепей.
Если же есть цепь в которой одно ребро (u, v), то переберем, какую из вершин, инцидентных этому ребру, мы возьмем в максимальную антицепь (также переберем вариант, когда не берем ни одной вершины). Пусть это вершина v. После этого, выкинем из рассмотрения данную вершину и все вершины, которые достижимы из v и из которых достижима v. После этого граф превратится в цепочку, на которой можно за линейное время динамическим программированием найти размер максимальной антицепи. Покажем, как это сделать.
Выпишем все вершины в цепочку и пронумеруем слева направо числами от 1 до k. После этого будем считать величину di — размер максимальной антицепи, среди вершин с номерами j ≥ i. Тогда, если i > k, то di = 0. Иначе мы можем пропустить i-ую вершину и улучшить величину di значением di + 1. Также мы можем попробовать взять i-ую вершину в ответ. В этом случае нужно пропустить все вершины, которые либо достижимы из i-ой, либо из которых достижима i-ая, взять ответ от следующей, прибавить к нему единицу и попробовать улучшить ответ.











Идея решения Е: сначала будем жадно выбирать вершины, которые находятся "внутри" цепи (есть как входящая, так и выходящая дуга), записывать их в ответ и с помощью dfs отмечать как "запрещенные" те вершины, которые находятся в той же цепи. Когда "внутренние" вершины закончатся — будем жадно брать любые другие вершины (которые в начале или в конце цепочки), если они еще не запрещены, и опять с помощью dfs "запрещать" соответствующие цепи.
Исходник: 4731928. Это правильное решение?
kak chasto ispolzueш asdfasdfsdadsg?
мета: //#define free asdfasdfsdadsg
такое чувство, что не в первый раз читаю задачу D :)
На Снарке она была, к примеру.
http://codeforces.net/problemset/problem/266/B
translation to English?
it will come soon)
Первое предложение в разборе D. Удалять 'F' в начале не нужно, так как операция удаления очень медленная O(length(S)), а можно просто в переменную Beg присвоить индекс первого 'M'.
Это наверное и имелось в виду под удалением.
In fact we have the strict inequality: for every ti > ti - 1
problem B can someone tell me why this code gives wrong answer ? the expected answer is so close !! http://codeforces.net/contest/353/submission/4736607
Read the comments here and you'll understand your mistake.
Good alanysis for problem D
Спасибо, за быстрый разбор!
I solve the problem E using matching
I solve the problem E using Matching
That's too slow. There is no (not even closely) linear algorithm for matching, so you'd TLE. But in this case, the graph we're given is composed purely of a cycle of cliques connected in some vertices, on which a greedy idea works well.
But he did. Look at this nice solution.
It didn't TLE probably because of special structure of the graph.
During the contest, I did it using matching too, via Hopcroft-Karp algorithm, and some friend of mine did the same. Here are our submissions:
4735010
4735373
My question is, why this doesn't TLE? Why this graph particular structure allow that? In Wikipedia I could only find that "for random graphs it runs in near-linear time.". Are the tests weak?
I actually really like this round especially Problem D. It took me a before I could build up all the ideas to solve it. My track of thoughts is like:
1. The answer is the number of seconds needed to move the last girl to the finish place.
2. The number of seconds needed for
girl iis at least the number of seconds needed forgirl i - 1+ 1.3. The number of seconds needed for
girl iis at least the distance between the initial position and the finish position.4. Each
girl iwill move as soon as she can, so she will be right at the back of thegirl i - 1or take at mostdist(i)seconds to follow thegirl i - 1.so we can calculate the
T(i) = max(T(i-1) + 1, dist(i))and the answer is justT(lastGirl).how you computed dist[i]?
dist[i] is just the distance between the initial position and the finish position (You already know the finish position of each girl).
В задаче А достаточно считать не сумму всех x и сумму всех y, а количество нечётных x и нечётных y?
Да. Более того, достаточно посчитать "чётное ли количество нечётных элементов вверху и внизу" и "есть ли хоть одна кость, нечётная с одной стороны и чётная с другой."
E can be solved by greedy, also in O(N). Let's count the lengths (as number of vertices) of individual chains (counted cyclically).
Every chain of length 3 adds 1 to the answer. That's because we could always choose a vertex from it that doesn't belong to any other chain instead of one of the side vertices that do belong to one, or instead of not choosing any vertex at all.
Now, we're left with either just a cyclic sequence of chains of length 2 (input 01010101...01 or reverse), for which the answer is the (length of the input string)/2, or some sequences of chains of length 2, each bordered by chains of length 3 on both sides. Greedy approach works here, too: no 2 chosen vertices from any such sequence can be adjacent, and we can't choose from the border. That means we can choose at most (length of such sequence-1)/2.
Was beaten hardly by problem B!! :( A great round though, I have learnt a lot!
I use a similar approach in probem D, i try to move the boys though:
for each boy, we know his initial and final position, thats the minimum time for this boy to move Actually it's the # of girls initially behind this boy
for each boy, if in the moving progress he has to stand and wait next boy to move, actually he can start in a later time so that he won's stop until arrive his final position, I call this the start time of the boy
For step 2 we can greedily precompute, and the ans is max(start time + # of girls behind) among all boys
Here's my code: 4742830
I use same basic idea, the difference is only on implementation, I didn't store that much information. here is my solution: 4735037
Моё решение Е: пометим все вершины, у которых оба ребра выходящие либо оба входящие. Если имеются 3 подряд идущих помеченных вершины — удаляем пометку у средней. Если после этого имеются 2 рядом стоящие помеченные вершины — удаляем пометку у любой из них. Всё это делается за линейное время. Кол-во оставшихся помеченных вершин и есть ответ.
http://codeforces.net/contest/353/submission/4745339 this code is wa for "011001" but it is accepted.
english please
I get wrong answer at Div2 D — Queue with this source, but I can't figure out why because of the large input. Could somebody give me a hint?