Meet a problem, but can't find solutions on internet. I know here are smartest people, so hope can get some help.
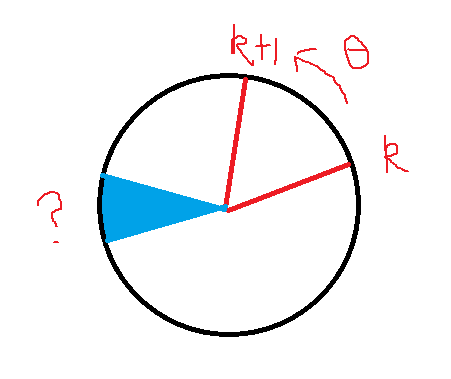
The problem is, starting from 0 degree, we rotate theta every time, theta is a floating point, like 33.7 degree. So now we have an array of angle with length of n, r = [0, theta, 2*theta, ..., (n-1)*theta] (wrap to [0..2*PI]).
And we are given an start index a and end index b, how can we quickly find all indices in [a..b] whose angle fall into angel range [t1..t2] (the blue area)? There could be many queries.
Really thanks for any idea, I can only think out iterating all indices one by one.











Auto comment: topic has been updated by TuanGe (previous revision, new revision, compare).
Auto comment: topic has been updated by TuanGe (previous revision, new revision, compare).
I just realize I can use sqrt decomposition. Divide
rinto $$$\sqrt{n}$$$ parts, and sort all elements in one part.Or just sort indexes by i*theta%2pi and answer linear to answer length.
Yes, should mod 2*pi, forget to mention
You can just sort all elements in this way. Than find ‘a’ by binary search and collect everything up to ‘b’.
Wait, if we sort all elements by i*theta%2pi, then the index from
atobis not continuous. And we also can't findausing binary search.You preserve index-value relation with pairs or map, or any other way:
N = 8, theta = 0.6pi, arr = [0, 06.pi, 1.2pi, 1.8pi, 2.4pi, 3.0pi, 3.6pi, 4.2pi]
After pairs sort: [(0.0, 0), (0.2pi, 7), (0.4pi, 4), (0.6pi,1), (pi, 5), (1.2pi, 2), (1.6pi, 6), (1.8pi,3)]. Pair.second is initial index. Now can you can do binary search.
Yes, but there is also an index constraint. We want to find indices in
[a..b]Ah, now I got it. We have two coordinates here. Well, we could think of treap (cartesian tree) here… But since we need every index, and not their count, we also could still stick up to sorting :) with same complexity. Initial one, given in problem (but maybe with angles mod’ed ti 2pi). When you are on angle arr[a] and want to get to sector-t1-t2, you know you should jump either ((2pi + t1 — arr[a])%2pi(to make sure its positive)/theta; or to next index after it. So you can find a, calc step to angle-t1, jump to that index, take all (or one, or none) indexes before angle-t2, than calc-and-jump to t1 again, until you reach index b. Thought treap will performe better if t2-t1 is less then theta.
Thanks for discussing!
Not sure how to use treap here. But I should mention the value in problem.
t2-t1=0.05, theta=3.73, both in radian. And it is floating points, so it is a little hard to decide how to jump....I would like to know what the constraints are but assuming n is up to like 1e6, what we could do is take the modulo of the angles and use coordinate compression on them. After that, we could use a persistent segtree to the answer from 1 to b and subtract it from the answer from 1 to a-1
Actually it is not an algorithm problem, but n can be very large, about 1e7.
Sorry can you explain a little more? So what information we should store in leaf? And since we need a list of indices, I think it will be expensive to remove indices [1..a-1] from [1..b]
First, please be more specific about the problem or link the place you found it. If you actually need a list of all the indices it would be O(n) per query to get that anyways so the optimal solution would be iterating through the indices. We have no way of knowing the restrictions of the problem that could make the problem more interesting because you're transcribing very limited information.
But about what you asked, i was thinking the problem was about getting the size of the answer. In each leaf there would be the ammount of indices with that angle value and since a persistent segtree can store all the versions of itself it would be possible to get it in O(logn).
Thanks for discussing and sharing your idea about segemnt tree! This problem is a simplified version that I meet in work.
For the original problem, if you are interested, I can describe that (actually not so important). For fibonacci lattice on a sphere, I want to find all point indices in an area (
theta_lo <= theta <= theta_hi, phi_lo <= phi <= phi_hi).And I just realize I can divide all these angles into $$$\sqrt{n}$$$ blocks, and sort all indices by their
angles % 2pi. Then for a query[a..b], if part of it fall in some block, then I can use binary search to find start and end position, and get all elements in that range. In this way I don't need to iterate all indices between[a..b].