Interesting Problem on Application of Stack
Hello everyone, This is my first blog entry on Codeforces. I want to share with you all an interesting problem based on application of stack. I came across the question in hiring process and have my detailed accepted solution approach and code.
Question:
Given an integer array A of length n.Find the sum of maximum of contiguous subarray times the length of the subarray for each subarray modulo 10^9+7. 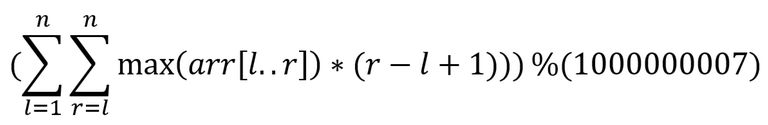
Constraints:
1<= n <= 10^5
1<= A[i] <= 10^9 , 1<= i <=n
Note: Array may have duplicate elements.
sample input 1
3
2 3 1
27
subarrays are
[2] ans=2
[3] ans=3
[1] ans=1
[2,3] ans=6
[3,1] ans=6
[2,3,1] ans=9
total=2+3+1+6+6+9=27
sample input 2
4
2 3 4 5
85
sample input 3(important case)
3
2 1 2
19
Approach:
First thing comes in mind seeing the contiguous subarray maximum is about the application of stack(refer problem:problem). We will take such a subarray in which A[k] is maximum (we will take subarray such that elements left to index k is less than or equal to A[k] and right to k is strictly less than A[k] to avoid extra ans in case of duplicate).
we consider the structure as:
arr[l] , arr[l+1],.....,arr[k],.....arr[r]
Here l is the leftmost index upto which arr[k] is the maximum element. i.e all the elements from index l to k-1 are smaller than or equal to element at index k. r is the rightmost index upto which arr[k] is the maximum element. i.e all elements from index k+1 to r are strictly smaller than element at index k.
To get this l and r we would use application of stack for finding nearest greater in left and right.
so from above structure how many contiguous subarray we can form with the condition to include element at index k.
total = (no. of elements in left +1) x (no. of elements in right +1)
total=(k-l+1) x (r-k+1)
but our motive isn't just to find count but we also need to find summation of length of all possible subarray in which arr[k] is maximum. so similarly using above casework we can do following:
let us make the subarray having leftmost end at k and rightmost end vary from k to r. we will get
arr[k..k] ,arr[k..k+1] ,arr[k..k+2],..... , arr[k...r]
so length summation of above subarrays are
sum = sum[0] = 1 + 2 + 3 + 4 + ........+ (r-k + 1)
using AP summation we get
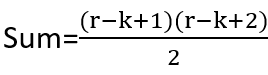
similarly we make the subarray having leftmost end fix at k-1 and rightmost end may vary from k to r. we will get
arr[k-1..k] , arr[k-1..k+1] ,...... , arr[k-1...r]
so length summation would be
sum[1] = 2 + 3 + 4 + 5 + ....... + ( r-k + 2)
we can rewrite it as
sum[1] = ( 1 + 1 ) + ( 1 + 2 ) + ( 1 + 3 ) + ( 1 + 4 ) + ...... + ( 1 + r-k + 1)
from above seperate all the extra one we get
sum[1] = 1 + 2 + 3 + .... + ( r-k + 1 ) + ( r-k + 1 ) x 1
hence
sum[1] = sum[0] + ( r-k + 1) x 1
similarly for leftmost to be at k-2 and rightmost at k to r
we get
sum[2] = 3 + 4 + 5 + ....... + ( r-k + 3)
seperating out 2 from each we get
sum[2] = sum[0] + ( r-k + 1 ) x 2
Generalizing above equation we get
for any i between 1 to k-l having leftmost end at k-i and rightmost end from k to r we get
sum[i] = sum[0] + i x ( r-k + 1)
But we need the summation of all the length of subarray so summing up all sum[i] , i from 0 to k-l would give us length sum
Let it be Len[k] for particular k
we get Len[k] = sum[0] + sum[1] + sum[2] +...... + sum[k-l]
we can rewrite it as
Len[k] = sum[0] + (sum[0] + ( r-k + 1) x 1) + (sum[0] + (r-k + 1) x 2)+.....+ (sum[0] + ( r-k + 1) x( k-l) )
seperating and simplifying we get
Len[k] = ( k-l + 1) x (sum[0]) + ( r-k + 1) x [ 1 + 2 + 3 ....+ ( k-l)]
Len[k] = ( k-l + 1) x (sum[0]) + [ (r-k + 1) x (k-l) x (k-l + 1)] / 2
usefull things we got
Len[k] = ( k-l + 1) x (sum[0]) + [ (r-k + 1) x (k-l) x (k-l + 1)] / 2
now we have length summation in which arr[k] is maximum what is left is just to multiply arr[k] in length and add it to final answer
ans[k] = arr[k] x Len[k]
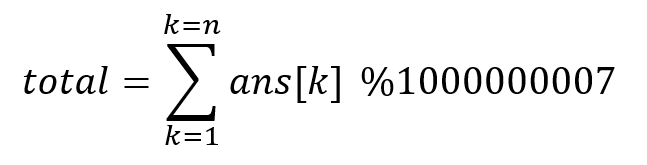
Note:
All the calculation should be performed under modulo to avoid overflow
Implementation
Time Complexity: O(n)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll mod=1000*1000*1000+7;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
//following zero based indexing
ll arr[n];
for(int i=0;i<n;i++){
cin>>arr[i];
}
//application of stack
stack<ll> s1,s2;
vector<int> left,right;
//to find index in left
for(int i=0;i<n;i++){
while(!s1.empty() && arr[s1.top()]<=arr[i]){
s1.pop();
}
if(s1.empty()){
left.push_back(-1LL);
}
else{
left.push_back(s1.top());
}
s1.push(i);
}
//to find index in right
for(int i=n-1;i>=0;i--){
while(!s2.empty() && arr[s2.top()]<arr[i]){
s2.pop();
}
if(s2.empty()){
right.push_back(n*1LL);
}
else{
right.push_back(s2.top());
}
s2.push(i);
}
reverse(right.begin(),right.end());
//our approach
ll total=0;
ll Len[n];
ll ans[n];
for(int k=0;k<n;k++){
ll r=right[k]-1LL;
ll l=left[k]+1LL;
ll sum=(r-k+1LL)*(r-k+2LL);
sum/=2LL;
sum%=mod;
Len[k]=(k-l)*(k-l+1LL);
Len[k]/=2LL;
Len[k]%=mod;
Len[k]=Len[k]*(r-k+1LL);
Len[k]%=mod;
Len[k]=(Len[k]+((k-l+1)*sum)%mod)%mod;
ans[k]=(arr[k]*Len[k])%mod;
}
for(int k=0;k<n;k++){
total=(total+ans[k])%mod;
}
cout<<total<<endl;
return 0;
}
import sys
input = lambda: sys.stdin.readline().strip("\r\n")
mod = 10**9 + 7
#using zero based indexing
n = int(input())
arr = list(map(int, input().split()))
#application of stack (ngl,ngr)
s1,s2 = [],[]
left,right = [],[]
#to find index in left
for i in range(n) :
while (s1 != [] and arr[s1[-1]] <= arr[i]) :
s1.pop()
if (s1 == []) :
left.append(-1)
else :
left.append(s1[-1])
s1.append(i)
#to find index in right
for i in range (n-1,-1,-1) :
while (s2 != [] and arr[s2[-1]] < arr[i]) :
s2.pop()
if (s2 == []) :
right.append(n)
else :
right.append(s2[-1])
s2.append(i)
right = right[::-1]
#our approch
total = 0
Len = [0 for i in range(n)]
ans = [0 for i in range(n)]
for k in range (n) :
r = right[k] - 1
l = left[k] + 1
Sum = (r-k+1)*(r-k+2)
Sum //= 2
Sum %= mod
Len[k] = (k-l)*(k-l+1)
Len[k] //= 2
Len[k] %= mod
Len[k] = Len[k]*(r-k+1)
Len[k] %= mod
Len[k] = (Len[k] + ((k-l+1)*Sum)%mod)%mod
ans[k] = (arr[k]*Len[k])%mod
for k in range (n) :
total = (total + ans[k])%mod
print(total)
Drop a Query or other approaches in Comment section.
Suggestions are welcomed.










Awesome problem and even an incredible solution.
I was thinking of another approach using Binary Search.
Approach:-
In total there will be Log N binary division, and each stage it will be O(1) if used Sparse Table for fetching the maximum inside the range.
Building up Sparse Table would take NlogN time and space.
Total T.C :- NlogN
yeah looks interesting but in worst case time complexity won't be log N
Consider the case as:
5
3 3 3 3 3
in this case you would end up making 5 division in worst case
add factor of precomputation of sparse table as well
I believe there is a very similar COCI problem, but I can't find it right now. I will update this post once I find it.
yeah sure, I will add the link once you update it
COCI ?
go to following link
I believe you are referring to this problem: https://dmoj.ca/problem/coci14c2p6
the problem you (andrewtam) mentioned seems much difficult problem than i discussed above..
If I am not wrong it would require much more advance data structure like segment tree with Lazy Propagation along with application of stack which we have used.
i also thought same like u , but i splitted the above equation into 3 parts like r,-l,+1 and applying summations, also u explained really well
great!!...
I tried the problem myself without the use of stacks, here is my overcomplicated approach. (coordinate compression + standard fenwick tree) (I'm not 100% about the correctness)
hey Ante0417
I appreciate your effort but its giving wrong answer on below case
10
5 6 5 5 4 10 15 7 6 15
Expected output:
2835
Oh that's unfortunate, turns out that the problem lies with my routine for determining what the two closest strictly larger values are for each element x.
yeah Ante0417 while finding closest greater element in left for the element at index 8(i.e 6).. Your code is giving index 6 but it should be index 7
This is actually an aplication of the solution to the maximum rectangle in a histogram problem. I really like it and its cool that you were able to reach this without seeing anything about it before.
Yeah, I just went through the basics along with mathematical manipulation to get it solved...
I got stuck on the overlap part If find (by stack) left[i] --> <=A[i] and Right[i] --> <=A[i] But there we have many overlap I dont figure out how to handle By seeing your soln i got idea that we have to limit R[i] --> <A[i] so that other is calculated by next similar Thanks for that idea
Yeah that was main learning to avoid overlaps