Interesting Problem on Application of Stack
Hello everyone, This is my first blog entry on Codeforces. I want to share with you all an interesting problem based on application of stack. I came across the question in hiring process and have my detailed accepted solution approach and code.
Question:
Given an integer array A of length n.Find the sum of maximum of contiguous subarray times the length of the subarray for each subarray modulo 10^9+7. 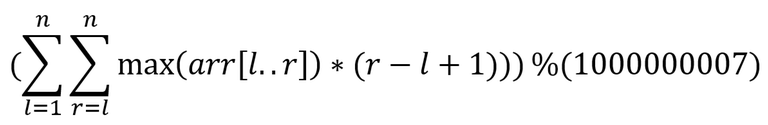
Constraints:
1<= n <= 10^5
1<= A[i] <= 10^9 , 1<= i <=n
Note: Array may have duplicate elements.
sample input 1
3
2 3 1
27
subarrays are
[2] ans=2
[3] ans=3
[1] ans=1
[2,3] ans=6
[3,1] ans=6
[2,3,1] ans=9
total=2+3+1+6+6+9=27
sample input 2
4
2 3 4 5
85
sample input 3(important case)
3
2 1 2
19
Approach:
First thing comes in mind seeing the contiguous subarray maximum is about the application of stack(refer problem:problem). We will take such a subarray in which A[k] is maximum (we will take subarray such that elements left to index k is less than or equal to A[k] and right to k is strictly less than A[k] to avoid extra ans in case of duplicate).
we consider the structure as:
arr[l] , arr[l+1],.....,arr[k],.....arr[r]
Here l is the leftmost index upto which arr[k] is the maximum element. i.e all the elements from index l to k-1 are smaller than or equal to element at index k. r is the rightmost index upto which arr[k] is the maximum element. i.e all elements from index k+1 to r are strictly smaller than element at index k.
To get this l and r we would use application of stack for finding nearest greater in left and right.
so from above structure how many contiguous subarray we can form with the condition to include element at index k.
total = (no. of elements in left +1) x (no. of elements in right +1)
total=(k-l+1) x (r-k+1)
but our motive isn't just to find count but we also need to find summation of length of all possible subarray in which arr[k] is maximum. so similarly using above casework we can do following:
let us make the subarray having leftmost end at k and rightmost end vary from k to r. we will get
arr[k..k] ,arr[k..k+1] ,arr[k..k+2],..... , arr[k...r]
so length summation of above subarrays are
sum = sum[0] = 1 + 2 + 3 + 4 + ........+ (r-k + 1)
using AP summation we get
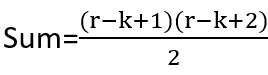
similarly we make the subarray having leftmost end fix at k-1 and rightmost end may vary from k to r. we will get
arr[k-1..k] , arr[k-1..k+1] ,...... , arr[k-1...r]
so length summation would be
sum[1] = 2 + 3 + 4 + 5 + ....... + ( r-k + 2)
we can rewrite it as
sum[1] = ( 1 + 1 ) + ( 1 + 2 ) + ( 1 + 3 ) + ( 1 + 4 ) + ...... + ( 1 + r-k + 1)
from above seperate all the extra one we get
sum[1] = 1 + 2 + 3 + .... + ( r-k + 1 ) + ( r-k + 1 ) x 1
hence
sum[1] = sum[0] + ( r-k + 1) x 1
similarly for leftmost to be at k-2 and rightmost at k to r
we get
sum[2] = 3 + 4 + 5 + ....... + ( r-k + 3)
seperating out 2 from each we get
sum[2] = sum[0] + ( r-k + 1 ) x 2
Generalizing above equation we get
for any i between 1 to k-l having leftmost end at k-i and rightmost end from k to r we get
sum[i] = sum[0] + i x ( r-k + 1)
But we need the summation of all the length of subarray so summing up all sum[i] , i from 0 to k-l would give us length sum
Let it be Len[k] for particular k
we get Len[k] = sum[0] + sum[1] + sum[2] +...... + sum[k-l]
we can rewrite it as
Len[k] = sum[0] + (sum[0] + ( r-k + 1) x 1) + (sum[0] + (r-k + 1) x 2)+.....+ (sum[0] + ( r-k + 1) x( k-l) )
seperating and simplifying we get
Len[k] = ( k-l + 1) x (sum[0]) + ( r-k + 1) x [ 1 + 2 + 3 ....+ ( k-l)]
Len[k] = ( k-l + 1) x (sum[0]) + [ (r-k + 1) x (k-l) x (k-l + 1)] / 2
usefull things we got
Len[k] = ( k-l + 1) x (sum[0]) + [ (r-k + 1) x (k-l) x (k-l + 1)] / 2
now we have length summation in which arr[k] is maximum what is left is just to multiply arr[k] in length and add it to final answer
ans[k] = arr[k] x Len[k]
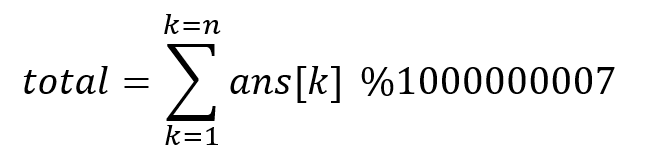
Note:
All the calculation should be performed under modulo to avoid overflow
Implementation
Time Complexity: O(n)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll mod=1000*1000*1000+7;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
//following zero based indexing
ll arr[n];
for(int i=0;i<n;i++){
cin>>arr[i];
}
//application of stack
stack<ll> s1,s2;
vector<int> left,right;
//to find index in left
for(int i=0;i<n;i++){
while(!s1.empty() && arr[s1.top()]<=arr[i]){
s1.pop();
}
if(s1.empty()){
left.push_back(-1LL);
}
else{
left.push_back(s1.top());
}
s1.push(i);
}
//to find index in right
for(int i=n-1;i>=0;i--){
while(!s2.empty() && arr[s2.top()]<arr[i]){
s2.pop();
}
if(s2.empty()){
right.push_back(n*1LL);
}
else{
right.push_back(s2.top());
}
s2.push(i);
}
reverse(right.begin(),right.end());
//our approach
ll total=0;
ll Len[n];
ll ans[n];
for(int k=0;k<n;k++){
ll r=right[k]-1LL;
ll l=left[k]+1LL;
ll sum=(r-k+1LL)*(r-k+2LL);
sum/=2LL;
sum%=mod;
Len[k]=(k-l)*(k-l+1LL);
Len[k]/=2LL;
Len[k]%=mod;
Len[k]=Len[k]*(r-k+1LL);
Len[k]%=mod;
Len[k]=(Len[k]+((k-l+1)*sum)%mod)%mod;
ans[k]=(arr[k]*Len[k])%mod;
}
for(int k=0;k<n;k++){
total=(total+ans[k])%mod;
}
cout<<total<<endl;
return 0;
}
import sys
input = lambda: sys.stdin.readline().strip("\r\n")
mod = 10**9 + 7
#using zero based indexing
n = int(input())
arr = list(map(int, input().split()))
#application of stack (ngl,ngr)
s1,s2 = [],[]
left,right = [],[]
#to find index in left
for i in range(n) :
while (s1 != [] and arr[s1[-1]] <= arr[i]) :
s1.pop()
if (s1 == []) :
left.append(-1)
else :
left.append(s1[-1])
s1.append(i)
#to find index in right
for i in range (n-1,-1,-1) :
while (s2 != [] and arr[s2[-1]] < arr[i]) :
s2.pop()
if (s2 == []) :
right.append(n)
else :
right.append(s2[-1])
s2.append(i)
right = right[::-1]
#our approch
total = 0
Len = [0 for i in range(n)]
ans = [0 for i in range(n)]
for k in range (n) :
r = right[k] - 1
l = left[k] + 1
Sum = (r-k+1)*(r-k+2)
Sum //= 2
Sum %= mod
Len[k] = (k-l)*(k-l+1)
Len[k] //= 2
Len[k] %= mod
Len[k] = Len[k]*(r-k+1)
Len[k] %= mod
Len[k] = (Len[k] + ((k-l+1)*Sum)%mod)%mod
ans[k] = (arr[k]*Len[k])%mod
for k in range (n) :
total = (total + ans[k])%mod
print(total)
Drop a Query or other approaches in Comment section.
Suggestions are welcomed.









