Заметим, что решения не существует, если самый дешевый способ стоит больше n. В противном случае всегда можно доплатить за любое угощение, дополнив суммарную стоимость до n.
Найдем самый дешевый способ. Очевидно, что каждой вахтерше лучше покупать то угощение, минимальная цена которого меньше. То есть, если есть вахта с параметрами a b c d, то стоимость минимального подкупа будет min(a, b) + min(c, d). Выберем вахту с наименьшей минимальной стоимость подкупа. Если она больше n, ответ -1. Иначе, ответом может быть, к примеру: Номер вахты, min(a, b), n–min(a, b).
Дима успевает сделать спокойно k–1 дело, то есть Инна всегда ругает его за k-ое дело, начиная с выбранного Димой первого дела. Таким образом, ответ для дел с одинаковым остатком от деления на k будет одинаковым, вывести нужно ответ с минимальным номером первого дела, поэтому достаточно посчитать суммы “руганий” для дел 0, 1... k–1. Это можно сделать к примеру так: Завести массив int sum[k]. И при считывании числа сразу определять его в соответствующую ячейку:
sum[I mod k] + = a[i]. Теперь осталось выбрать первое i такое, что sum[i] минимальное.
Сложность решения O(N).
Будем поддерживать динамику d[num][balance] где num – последний рассмотренный фрукт, balance – разница между суммами выбранных калорийностей и вкусностей. Умножим все b на k. Тогда ответом будет d[n][0].
d[num][balance] = максимально возможной сумме вкусностей.
Переход: из d[num][balance] можно осуществить так:
d[num + 1][balance] = max(d[num + 1][balance], d[num][balance]) – если мы не берем фрукт.
d[num + 1][balance + a[i] - b[i]·k] = max(d[num + 1][balance + a[i] - b[i]·k], d[num][balance] + a[i]) – если берем.
На самом деле, баланс может быть отрицательным, поэтому в языках программирования, не поддерживающих отрицательную индексацию, индексы баланса нужно сдвинуть на самое большое отрицательное число, которым может стать баланс. Если баланс – сумма каллорийностей минус сумма вкусностей, то это сумма всех вкусностей всех фруктов.
Очевидно, что лояльность пути – это ширина диапазона, с которым его можно пройти, а диапазон этот – пересечение диапазонов ребер пути. Это выплывает из того, что числа является валидным для пути, если с ним можно пройти через все ребра. Переберем все ребра графа, пусть левая граница диапазона на ребре – это левая граница пересечения. Это значит, что мы не можем использовать ребра, у которых левая граница не больше нашей. Переберем все правые границы, считая ответом диапазон с зафиксированной ранее левой границей и выбранной нами правой. Такой ответ существует, если можно пройти из первой вершины в последнюю с выбранными ограничениями. Проверим граф на связность выбирая только ребра с левой границей не больше нашей, и правой границей не меньше нашей. Если граф связный, обновляем ответ. Заметим, что правую границу можно перебирать с помощью бин поиска, таким образом итоговая сложность решения O(M2·logM).
366E — Дима и волшебная гитара
Задача имеет несколько решений. Опишу авторское, с остальными вы можете ознакомиться, посмотрев решения участников. Очевидно, что для нахождения ответа нужно посчитать матрицу maxDis[k][k], где maxDis[i][j] – максимальная сложность перехода между нотами i и j.
Тогда останется пройтись по песне, и обновлять ответ для каждой пары соседних нот. Давайте подумаем, как можно быстро посчитать матрицу.
Для каждого места (x1, y1) на гитаре переберем все места (x2, y2) такие, что y2 ≤ y1.
Если (x2 ≤ x1) расстояние будет x1–x2 + y1–y2. И значит, нас интересует минимальное значение x2 + y2 в подматрице от (0, 0) до (x, y).
Если (x2 ≥ x1) расстояние будет x2–x1 + y1–y2. И значит, нас интересует максимальное значение x2–y2 в подматрице от (n–1, 0) до (x, y).
Будем считать эти значения для каждой ноты. Памяти нужно слишком много, но можно хранить только предыдущую строчку динамики для каждой ноты. Для каждой ячейки обновим динамику для всех нот, и для нашей ноты (которая и лежит в этой ячейке) сравним значение (i + j) или (i–j) с текущим в динамике.
Сложность O(N·M·K)
Я, видимо, неправильно понял задачу, но перечитывание не помогло. Подскажите, пожалуйста, почему нижеприведённый тест не валит авторское решение?
upd. Укоротил тест.
Мы считаем динамику
A[i][j][k] — минимальное I + J (I <= i, J <= j, guitar[I][J] = k).
B[i][j][k] — максимальное I — J (I <= i, J <= j, guitar[I][J] = k).
A[0][4][4] = 0; поэтому matrix[3][4] = (0 + 4 — A[0][4][4]) = 4.
Надеюсь, объяснил.
Простите, если разбор или ответ не внятный, очень устал =)
Правильно ли я понимаю, что: maxDis[1][4] = 2, maxDis[4][3] = 4? Если так, то у вас получится ответ 6, в то время как правильный 5. Или здесь правильный ответ 6? Или я решение не понял? Вы тоже простите, если что, сегодня весь вечер туплю.
Начнем с того, что ответ — расстояние между (1, 5) и (1, 1) — 4.
Напомню, что сложность песни — это максимальная сложность перехода между соседними (не сумма)
Ой, спасибо, ещё раз перечитал задачу, и теперь уже понял. Так она куда проще. Я же решал задачу, где сложность песни была сумма переходов между нотами. Она немного посложнее :\
Спасибо за замечательные задачи!
I (but not just me, as I noticed from looking at others' codes) have a cool solution of E:
Imagine that we want to calculate the max. distance of 2 tones a, b. Take tone a at (x1, y1) and b at (x2, y2); notice that |x1 - x2| + |y1 - y2| is the maximum of ± (x1 - x2) ± (y1 - y2) for all signs, which leads to 4 possible expressions:
Instead of limiting ourselves to the correct expression, we can evaluate the maxima of all pairs of points with all 4 expressions, and the answer will still be the maximum of them all. Notice that all 4 are linear, so we just need to calculate the maximum and minimum of $x_1+y_1$ and x1 - y1 for all points of one tone; the result for 2 tones can be found by trying the maxima of all 4 expressions, which are (in that order)
Complexity: O(NM) :D
Please elaborate the part Notice that all 4 are linear, so we just need to calculate the maximum and minimum of x1 + y1 and x1 - y1 for all points of one tone;
We compute the numbers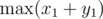
and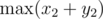 
and take their difference. Similarly for the other 3 expressions, and for any pair of tones (denoted here as "1" and "2").
For any linear function f (UTFG if you don't know about these) we have
Actually there is a simple soluton for problem D with complexity O(M ^ 2).
Tip: Two pointers instead of binary search.
Can u double-check the expressions in solution for task C?
Can someone please explain the solution to C? I did not understand the use of balance. I just thought of doing the following: For a pair (a,b), if a/b = k, it can be.included in our solution. For all pairs for which a/b!=k, check if adding the pair to the solution satisfies given conditions. If yes, include it in solution. We can choose nC2 pairs and do the above operations in O(n^2).
I still don't understand how to handle negative indices. Btw, it's Dynamic Programming.
Yes, I got that it is dp.
the second index (
balance) always lies between-100,000and+10,000. therefore, we can access theith element of an array by shifting indices likea[i+100000](here it'sdp[i][balance+100000]), or by using other data structures like map.Oh, ok thanks!
If you sort fruits by balance in descending order, you won't need this trick with index shifting. dp[n + 1][10 * 1000] would be sufficient
I can't understand how my solution with negative array indices is able to work. Code
Can you please explain the procedure if instead of considering a[i]-k*b[i], I would have considered k*b[i]-a[i]. I am getting WA on testcase 6. https://codeforces.net/contest/366/submission/184402801
One way is to use a third state variable which denotes the sign of the difference i.e, whether the difference is +ve or -ve. Here: 45877072
In D, what do you mean by ribs and boards?
i'm not sure, but i think rib means edge, and board means bound (i.e. left board = lower bound, right board = upper bound)
can somebody explain problem D solution
А в D, когда Сережа фиксирует путь, чтобы посчитать его лояльность, под путём он подразумевает конкретные рёбра, по которым пойдёт, или вершины, через которые пойдёт. При кратных рёбрах эти варианты дадут разный результат на таком тесте:
Судя по разбору, имеется в виду именно зафиксированный по рёбрам путь, но при чтении задачи это не было очевидно.
Да, имелись ввиду ребра. Если я не ошибаюсь, в сэмплах был тест с кратными ребрами.
В задаче С в последний формуле кажется опечатка!
=>
I don't like how A is worded,
"If a chocolate bar for some guard costs less than the minimum chocolate bar price for this guard is, or if a box of juice for some guard costs less than the minimum box of juice price for this guard is, then the guard doesn't accept such a gift."
By using "this guard" and "some guard", it can be read that out of all the guards, this guard's minimum chocolate price must be the minimum out of every guard.
you are absolutely correct there is a problem in this statement my solution is not working just because of this condition
I must say problem C is amazing, never seen any problem quite like it.
dp[i+1][summation + a[i]]<<=b[i];we will shift every summation of calories by b[i];ACCEPTED
Is it doable in a recursive way? Using Bitsit.