369A - Валера и тарелки
Будем действовать жадно. Пусть сейчас i-й день, и текущее блюдо типа 1. Тогда если у нас есть чистая глубокая тарелка, то воспользуемся ею. Иначе увеличим ответ. Если текущее блюдо типа 2, то мы сначала попробуем взять плоскую тарелку, а потом глубокую. Если чистых тарелок нет совсем, то увеличим ответ.
Авторское решение: 5306397
369B - Валера и олимпиада
В этой задаче требовалось найти такой массив a1, a2, ..., an, что верны условия:
- r ≥ a1 ≥ a2 ≥ ... ≥ an ≥ l;
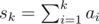 ;
;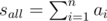 ;
;
Понятно, что сумму sk нужно распределить равномерно между первыми k элементами. Например, так:
remainder = (s_k mod k);
for(int i = 0; i < k; i++)
{
a_i = s_k / k + (remainder > 0);
remainder = remainder - 1;
}
Если k ≠ n, то аналогично нужно поступить с остальными элементами, причем распределить им нужно sall - sk.
Многие не учитывали случай k = n, в результате получали RE11.
Авторское решение: 5306414
369C - Валера и выборы
Рассмотрим все дороги, которые нам нужно отремонтировать. Пометим их концы u, v белым цветом. После этого, посчитаем простую динамику d[v] (v — вершина в дереве) на дереве, которая для каждой вершины в дереве посчитает количество белых вершин в поддереве. Это просто посчитать примерно так c помощью рекурсивной функции calc(v, prev) (v — текущая вершина, а prev — ее непосредственный предок):
calc(v, prev)
{
d[v] = 0;
if (white[v])
dv += 1;
для всех u, таких что существует ребро (u,v) или (v,u) u != prev:
calc(u, v);
d[v] += d[u];
}
После этого, добавим к ответу количество белых вершин v, для которых d[v] = 1
Авторское решение: 5306500
369D - Валера и дураки
Пусть p[A] — вероятность того, что дурак с номером A попадет, если совершит выстрел.
Заметим, что состояние очень просто описать парой чисел (A, B), где A — номер самого левого дурака, B — второго слева по порядку дурака. Понятно, что все дураки с индексами ≥ B останутся живы. Выполним bfs по этим состояниям.
Состояние (0, 1) достижимо в любом случае, потому что оно изначально. Поэтому сразу положим его в очередь. Далее, из текущего состояния в очереди мы можем перейти максимум в три состояния:
- (B + 1, B + 2) — только если p[A] > 0 и существует такой дурак с номером j ≥ B, у которого p[j] > 0.
- (A, B + 1) — только если p[A] > 0 и не существует такой дурак с номером j ≥ B, у которого p[j] = 100.
- (B, B + 1) — только если p[A] ≠ 100 и существует такой дурак с номером j ≥ B, у которого p[j] > 0.
После этого, достаточно посчитать количество состояний, расстояние до которых от (0, 1) не более чем k. Также нужно аккуратно учесть, что если остался один дурак, то он не совершает выстрелов.
Авторское решение: 5306516
369E - Валера и запросы
Давайте поддержим множество xs[y] — все отрезки, чьи правые границы в точности равны y. Теперь сведем нашу задачу к другой. Для каждого запроса посчитаем количество отрезков, которым не принадлежит ни одна точка. Пускай это значение v. Тогда ответ на запрос это n - v. Добавим к нашему запросу точки 0 и точку MV + 1, где MV = 1000000. Пусть точки запроса имеют вид x1 < x2... < xn. Рассмотрим xi и xi + 1. Пусть pi это количество отрезков которые лежат строго внутри xi и xi + 1. Тогда v = p1 + p2 + ... + pn - 1. Чтобы найти значения pi нужно поступить так. Рассмотрим все такие пары (x, xi + 1) по всем запросам и сложим их во второе множество xQ[r] — все пары, у которых правая граница равна r. Тогда чтобы узнать значения p для пар (xi, xi + 1) будем перебирать по возрастанию правую границу. Дополнительно будем поддерживать дерево Фенвика, которое умеет делать + = 1 в точке, и брать сумму на префиксе. Пусть i — текущая правая граница. Тогда мы можем узнать значение p для всеx пар (l, r), у которых правая граница равна i (l, i). Пусть j левая граница пары. Тогда ответом для пары будет значение S - sum(j), где S — количество добавленных в дерево Фенвика левых границ, а sum(j) — сумма на префиксе j. После этого, для текущей координаты нужно рассмотреть все отрезки, в множестве xs[i]. Пусть j левая граница отрезка. Тогда нам нужно сделать + = 1 в точке j в нашем дереве Фенвика. Итого, общая сложность решения 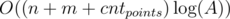 .
.
Авторское решение: 5306535











Всмысле
Если хотя бы одно условие не выполнилось, то ответ -1.? Вроде же ответ есть всегда?Задача B
Если хотя бы одно условие не выполнилось, то ответ -1в условии написаноГарантируется, что входные данные таковы, что ответ существует.Непонятно. И про -1 в условии нет.upd: ломали при n = k часто, у многих на 0 делилось в таких тестах.
Изначально предполагалось, что ответ -1 может быть. Разбор я написал давно, а условие про то, что решение существует добавил недавно. Чуть позже поправлю разбор.
Я единственный писал на Е персистентное дерево отрезков? :)
Nurlan123, а можно по-подробнее?
По E заходит стандартное решение с e-maxx — храним в каждой вершине дерева отрезков все отрезки, которые начинаются на этом интервале, и отвечаем на запрос за log^2.
А можно по-подробнее, пожалуйста?
Переходим к задаче "сколько отрезков расположены полностью между данными двумя точками", как написано в разборе.
Пусть у нас есть дерево отрезков, которое отвечает за левые концы интервалов из инпута. В самом простом и привычном дереве отрезков f(v) известно и определяется за О(1) — это какая-то сумма/максимум/минимум на отрезке, к примеру. И она лежит прямо в каком-то массиве сразу после построения дерева. В нашей же задаче при запросе "сколько интервалов с левыми концами в этом отрезке имеют правые концы левее х" — нас интересует своего рода f(v,x). Т.е. нам надо уметь узнавать, сколько из интервалов, левые концы которых принадлежат данному отрезку, имеют правые концы левее х.
Для конкретной вершины дерева отрезков это можно сделать за log бинарным поиском, если в вершине хранить отсортированный вектор правых концов для всех интервалов, левые концы которых принадлежат этому отрезку.
С этим приемом — задача выглядит как обычное RSQ, только в тот момент, когда в обычном RSQ мы сразу делаем return value[v];, здесь надо бинарным поиском еще найти это value для заданной правой границы.
Очень крутое решение у Вас! ) Спасибо!
В Е написал похожее решение, только за O(n + m):
Посчитаем два массива l и r, где l[i] — количество отрезков, у которых левая граница лежит в интервале [0; i], а r[i] — количество отрезков, у которых правая граница лежит в интервале [i; 1000000]. Тогда вполне понятно, как посчитать количество отрезков строго внутри интервала за O(1).
Жаль только, что где-то багу посадил =_=
И как же это сделать за O(1) ?
Пусть интервал задан двумя точками. Может, можно ещё проще, но я считал как
ans = n - left - right - (first + second - both), где:left— кол-во отрезков слева от первой точки;right— кол-во отрезков справа от второй точки;first— кол-во отрезков, пересекающихся с первой точкой;second— кол-во отрезков, пересекающихся со второй точкой;both— кол-во отрезков, пересекающихся с обоими точками.Тогда
first + second - both— кол-во отрезков, пересекающих хотя бы одну из точек по формуле включений-исключений. А итоговый ответ — все точки без тех, которые лежат слева от интервала, справа от интервала, или пересекаются хотя бы с одной из границ интервала.Количество же пересекающихся отрезков с некоторой точкой
xестьr[x] - (n - l[x]): смотрим, сколько отрезков заканчивается после точки, сколько начинается, вычитаем эти две величины и получаем то, что нужно.А both то как считать?
Тест снизу показал, почему мой способ подсчёта both не работает. На контесте же мне он казался безупречным, и многочисленные тревоги по поводу того, о чём сказал снизу автор, как-то сами умирали.
Считал же как
r[b] - (n - l[a]), где a, b — границы интервала.За О(1)? Круто.
Предположим, что у нас запрос на интервал 10 20.
И есть 2 отрезка, 5 25 и 12 18
Или лучше такие 2 отрезка, 5 18 и 12 25 — какая разница, массивы l и r ведь в обеих случаях одинаковые... Понятно, к чему я веду?
Да, я облажался. Вопросы по поводу сказанного тобой возникали у меня в голове во время написания решения, но я как-то не придавал им внимания, и всё мне казалось стопроцентно правильным, хотя сейчас я не понимаю, как я мог так тупить)
random_shuffle(ans.begin(), ans.end());dafuk :D
Isn't that Bogosort?
One iteration of Bogosort.
Redundant Input in "B" confused me :(
In Problem D
what os the difrrence between using BFS and Using Recursion ?!
because Bfs ACC but recursion WA
with the same code ?! http://ideone.com/WpPgn1
PRoblem D what is the Difrrence Between Using BFS and Using Recursion at the same code here ?! bfs get AC and recursion get WA !!! http://ideone.com/WpPgn1
BFS gives you the shortest path, while DFS (recursion) just tells you whether or not a path exists.
in this problem the path length is important because you want all states within a distance of
kfrom the start state. therefore DFS would not be a right solution.Hello guys,
I need a little help with the Varela and Fools problem.
Can you see my submission? When I compile and test with the first test case (on my machine, using g++), i get 7 as answer (correct answer), but the judge is saying that my code gives 4 as answer.
What can I do? http://codeforces.net/contest/369/submission/5324049
If you compile it with -pedantic flag it says something like
warning: ISO C++ forbids variable length array ‘p’So instead ofp[n]you should do something likep[3000].for problem D, each currently living fool shoots at another living fool with the smallest number (a fool is not stupid enough to shoot at himself). So the smallest number shoots whom? randomly or just the fool next to him? I think it is not clear. thanks
ah got it, thanks and sorry.
In Problem E solution i didn't understand the algorithm which calculates the value of pi, any help ?
Getting "Memory Limit Exceeded" in C. Please help
29529634
I am Using DFS, once a bad row is encountered say v->v+1, the program saves the corresponding leaf l in a set(by going deeper and deeper till leaf is encountered), this way all the bad roads from v+1 to l are also repaired.
you may have got
stack overflowduring recursion. I have gotMemory limit exceeded on test 6before:32189259.After purning inefficient dfs steps, I got
Accepted. just like this:32189351.60057569 is giving MLE, unable to figure out what to change.
I am also getting Memory Limit exceeded on test 6 260674620 could you help me figuring out this? and what steps have you taken?
For B, why don't we need to use l and r (the lower and upper limits)?
Can somebody share some different approach for C — Valera and Elections?
Let's call edge with 2 "Problem edge"
If any node having a Problem edge between it's parent and the subtree of that node doesn't have any Problem edge then this node must be included in the answer.
This can be solved using simple DFS.
refer this