370A - Ладья, слон и король

К задаче есть два подхода. Первый — три раза запустить поиск в ширину. Второй — более легкий, нужно лишь понять, что:

• Ладья может достичь любого поля не более, чем за два хода. Если стартовое и конечное поле находятся в одной строке или в одном столбце, то достаточно одного хода.
• Слон может достичь только клетки, окрашенные в тот же цвет, что и стартовая, и тоже не более чем за два хода. Если стартовое и конечное поле находятся на одной диагонали, то достаточно одного хода. Чтобы это выяснить, нужно проверить, что r₁ - c₁ = r₂ - c₂ ИЛИ r₁ + c₁ = r₂ + c₂.
• Королю достаточно сделать max(|r₁ - r₂|, |c₁ - c₂|) ходов.

    int r1, c1, r2, c2;
    cin >> r1 >> c1 >> r2 >> c2;
    if (r1 == r2 || c1 == c2) cout << 1; else cout << 2;
    cout << " ";
    if ((r1 + c1) % 2 != (r2 + c2) % 2) cout << 0; else {
        if (r1 + c1 == r2 + c2 || r1 - c1 == r2 - c2) cout << 1; else cout << 2;
    }
    cout << " ";
    cout << max(abs(r1 - r2), abs(c1 - c2)) << endl;

370B - Берляндское лото

В этой задаче полезно рассматривать карточки игроков как множества чисел. В таком случае, карточка a не может быть закрыта строго раньше карточки b, если b является подмножеством a. Таким образом, критерием того, что карточка может быть закрыта первой является тот факт, что не существует другой карточки, которая является ее подмножеством.

Так как карточек всего 100, то для каждой карточки можно перебрать все остальные, чтобы осуществить проверку. Проверку на подмножество можно делать совсем простым способом, например, так:

bool contains(vector<int> a, vector<int> b) // b in a?
{
    forn(i, b.size())
    {
        bool in = false;
        forn(j, a.size())
            if (a[j] == b[i])
                in = true;
        if (!in)
            return false;
    }

    return true;
}

370C - Варежки

Если максимальный цвет встречается не более 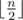раз, то каждый ребенок может получить левую и правую варежки разного цвета. Для этого отсортируем все левые варежки в порядке убывания частоты их цвета: для входа 1 2 1 2 3 1 3 3 1 получилось бы 1 1 1 1 3 3 3 2 2. Чтобы получить последовательность цветов правых варежек, сдвинем последовательность цветов левых варежек влево на количество самого популярного цвета (в примере это 4, поэтому получим 3 3 3 2 2 1 1 1 1). И теперь объединим эти две последовательности в пары (1 — 3, 1 — 3, 1 — 3, 1 — 2, 3 — 2, 3 — 1, 3 — 1, 2 — 1, 2 — 1). Легко показать, что при этом все пары будут состоять из варежек различного цвета.

Хорошо, ну а что же делать, если есть доминирующий цвет, который встречается слишком много раз? Применять тот же самый алгоритм! При его применении количество разноцветных пар будет наибольшим.

370D - Сломанный монитор

У этой задачи есть большое количество правильных решений, но еще больше у нее неправильных решений :)

Один из способов решить её такой. Легко видеть, что в правильном ответе найдется две противоположные стороны, на которых есть символ w. Если бы это было не так, то рамку можно было бы сжать до меньшего размена. Таким образом, размер рамки это dx или dy, где dx = maxx - minx + 1 and dy = maxy - miny + 1 (minx, maxx, miny, maxy — это соответствующие координаты левой/правой/верхней/нижней буквы w). Очевидно, размер искомой рамки равен максимуму из dx, dy.

Хорошо, размер рамки ясен, а как быть с её положением? Попробуем найти ее левый верхний угол.

Множество возможных координат x левого верхнего угла — это {minx, maxx - size + 1, 0}. В самом деле, давайте начнем двигать искомую рамку влево, пока это возможно. Либо она упрется в w левым или правым краем, либо в левую границу монитора.

Аналогично, множество возможных координат y левого верхнего угла — это {miny, maxy - size + 1, 0}.

Таким образом решение принимает вид:

find minx, maxx, miny, maxy
dx = maxx-minx+1, dy=maxy-miny+1
size = max(dx, dy)
foreach x in {minx, maxx-size+1, 0}
    foreach y in {miny, maxy-size+1, 0}
        if frame_correct(x, y, size)
            print answer
            exit algorithm

Всё что осталось сделать, это написать функцию frame_correct, которая проверяет, что рамка с левым верхним углом в (x, y) и размером size является ответом. Для этого достаточно пройти по ней и проверить, что все ее клетки находятся в границах монитора и количество w на рамке совпадает с их общим числом.

Описанное решение работает за O(nm).

370E - Летнее чтение

Для каждого номера книги, который присутствует в последовательности, найдем самое левое и самое правое вхождения: для каждого номера получился отрезок из позиций, на котором он точно должен быть записан. Понятно, что если два каких-то отрезка пересеклись, или же длина какого-то отрезка больше 5, то ответа не существует. Можно еще отдельно обработать случай, когда все числа — нули. Тогда дневник можно заполнить жадно, отдавая на все книги (кроме, возможно, одной), по два дня.

Итак, у нас есть несколько блоков из чисел и промежутки между ними. Будем решать задачу при помощи динамического программирования (ДП). Состояние будем описывать парой чисел (i, j): i означает номер блока из номеров книг (пронумеруем блоки слева направо), а j означает, до какой позиции числа из i-го блока будут идти в итоге (если после этого блока есть непустой промежуток свободных позиций, то сколько-то первый из них могут содержать такие же номера книг). Очевидно, что j - i не превосходит 5, поэтому количество состояний линейное. Пусть D(i, j) равно true, если можно корректно заполнить все пропуски до i-го блока при условии, что i-й блок распространится вправо вплоть до позиции j, и D(i, j) равно false в противном случае. Чтобы определить D(i, j), давайте переберем еще и то, насколько i-й блок распространится влево (очевидно, что таких способов всего несколько). Затем переберем позицию, до которой будет идти (i - 1)-й блок (т.е. зафиксируем состояние D(i - 1, k), где D(i - 1, k), конечно, равно true). Чтобы понять, возможен ли переход в ДП, нужно выяснить, можно ли корректно заполнить остаток промежутка между блоками. Пусть (i - 1)-й блок состоит из чисел x, i-й блок состоит из чисел y, а оставшаяся длина промежутка равна f. Тогда промежуток можно заполнить тогда и только тогда, когда 2·(y - x - 1) ≤ f ≤ 5·(y - x - 1).

Если вы осознали, как работает это ДП, то вам не составит труда понять, как получить ответ.