370A - Rook, Bishop and King

There are two approaches to this task. The first is use BFS to find the shortest path three times. The second is to notice that:

• A rook can reach the destination in one or two moves. If the starting and the destination fields are in the same row or column, one move is enough.
• A bishop can reach only fields that are colored the same as the starting cell, and can do this in at most two moves: if the starting and the destination fields are on the same diagonal, one move is enough. To find this out, check that r₁ - c₁ = r₂ - c₂ OR r₁ + c₁ = r₂ + c₂.
• A king should make max(|r₁ - r₂|, |c₁ - c₂|) moves.

    int r1, c1, r2, c2;
    cin >> r1 >> c1 >> r2 >> c2;
    if (r1 == r2 || c1 == c2) cout << 1; else cout << 2;
    cout << " ";
    if ((r1 + c1) % 2 != (r2 + c2) % 2) cout << 0; else {
        if (r1 + c1 == r2 + c2 || r1 - c1 == r2 - c2) cout << 1; else cout << 2;
    }
    cout << " ";
    cout << max(abs(r1 - r2), abs(c1 - c2)) << endl;

370B - Berland Bingo

It is good idea to think about cards as set of numbers. It is easy to see that card a can’t be finished before b if b is subset of a. So all you need is to find such cards (sets) which do not have other card (other set) as subset.

Since there are at most 1000 cards, you may iterate through all pairs and check that one card contains other in naive way like:

bool contains(vector<int> a, vector<int> b) // b in a?
{
    forn(i, b.size())
    {
        bool in = false;
        forn(j, a.size())
            if (a[j] == b[i])
                in = true;
        if (!in)
            return false;
    }

    return true;
}

370C - Mittens

Let’s show that if the most frequent color appears not more than 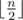times, than all children can get mittens of distinct colors. One way to construct such solution is to sort all left mittens in the order of decreasing frequency of their colors: for the input 1 2 1 2 3 1 3 3 1 we get 1 1 1 1 3 3 3 2 2. To obtain the sequence of right mittens, rotate the sequence of left mittens to the left by the maximum color frequency (in the example it is 4, so we get the sequence 3 3 3 2 2 1 1 1 1). Then just match the sequences (1 — 3, 1 — 3, 1 — 3, 1 — 2, 3 — 2, 3 — 1, 3 — 1, 2 — 1, 2 — 1). It can be easily shown that all pairs consist of distinct colors.

OK, but what to do if there is a dominating color that appears more than half times? Use exactly the same algorithm! It will maximize the number of pairs of distinct colors.

370D - Broken Monitor

There are a lot of correct approaches to solve the problem. But there are much more incorrect :)

One way to solve the problem is following. It is easy to see that in possible answer there are two opposite sides each containing w. In opposite case frame can be shrinked. So the size of frame is dx or dy, where dx = maxx - minx + 1 and dy = maxy - miny + 1 (minx, maxx, miny, maxy are coordinates of left/right/top/bottom ws). Obviously, you should choose max(dx, dy) as a size.

Now we know the size of the required frame. How to find it’s leftmost-topmost corner?

The set of possible xs is: minx, maxx - size + 1 and 0. Indeed, you may move frame to the left until it will abuts to w by left size/right size of abuts to the left side of monitor.

Similarly, the set of possible ys as y-coordinate of leftmost-topmost corner: miny, maxy - size + 1, 0.

Now the solution looks like:

find minx, maxx, miny, maxy
dx = maxx-minx+1, dy=maxy-miny+1
size = max(dx, dy)
foreach x in {minx, maxx-size+1, 0}
    foreach y in {miny, maxy-size+1, 0}
        if frame_correct(x, y, size)
            print answer
            exit algorithm

All you need is to write frame_correct. You may iterate through frame and check that all cells inside monitor and calculate the number of ws on it. If all the cells are inside and calculated number equals to total number of w, then return true.

This solution works in O(nm).

370E - Summer Reading

For each book number that is in the sequence, find the leftmost and the rightmost position of this number. In other words, for each such book number we find a segment of positions that should consist of this number. If for some pair of numbers there segments intersect, it is impossible to construct the answer. The same thing happens if some segment has length more than 5. It is reasonable to separately handle the case when all given numbers are zeroes. In this case, fill in the numbers greedily, spending 2 days on each book (probably, except the last one).

So, we have some blocks of numbers and gaps between them. Lets do the following DP: each state of DP is described by two values (i, j): i means the number of block (lets enumerate them consecutively), j means how far to the right will this block eventually extend (if there is a gap after this block, it is possible that we fill some prefix of this gap with the same book number that is in the block). It is clear that j - i will not exceed 5, so we actually can describe the state by values (i, j - i), which may sound more convenient. So, the number of states is linear. Lets say that D(i, j) is true if it it possible to correctly fill all the gaps that come before the i-th block, under condition that the i-th block extends to the position j, and D(i, j) is false otherwise. To calculate the value of D(i, j), lets try to extend the i-th block to the left in all (not so many) possible ways (to replace some number of consecutive zeroes that are in the gap just before the i-th block). Then, try to fix where the previous block can actually end (fix the state D(i - 1, k), where D(i - 1, k) is true, of course). To make a transition in DP, we should check whether it possible or not to fill the rest of the gap between the (i - 1)-th block and the i-th block. Lets say that (i - 1)-th block consists of number x, the i-th block consists of number y, and there are f still unfilled positions in the gap. Than the gap can be correctly filled if and only if 2·(y - x - 1) ≤ f ≤ 5·(y - x - 1).

If you understand this DP, it won’t be difficult for you to find out how to construct the answer from it.