LIS — Longest Increasing Subsequence
LCS — Longest Common Subsequence
Recently, at a colloquium in a class at Tinkoff I was given the task of finding the LCS of two permutations for nlogn. At first I tried to come up with something with hashes, but nothing worked, then I decided to link LIS and LCS. This can be done through the ordinal number of elements in the permutations (picture attached). You need to write down a sequence of numbers that denotes the number of occurrence of a character from the first permutation to the second. Thus, if we find the LIS of the resulting permutation of numbers, we get the LCS of these two permutations. LIS for nlogn can be found using a well-known algorithm that uses binary search. As a result, we get the asymptotics of nlogn.
Such an algorithm makes sense, since if you take any character in the source string, then in LCS the next character can only be the one that stands in this line after it, and at the same time in the second line it stands after equal to the previous. 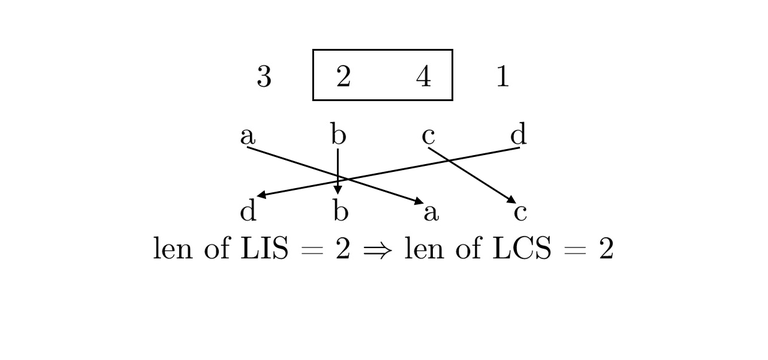











Ученики параллели С пишут блоги...
С'...
Чего, я вообще не знал что такая есть
104349D - Yet another permutation problem