Hi all!
I invite you to participate in the gym contest LU ICPC Selection Contest 2023 on Nov/08/2023 17:35 (Moscow time)! The onsite contest has been held on October 13th in Riga to select two teams from the University of Latvia to CERC 2023. Here's the headline of the local poster (in Latvian):

The contest has been prepared by me, cfk and Pakalns. Hopefully you'll find the problems interesting!
























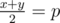 .
.
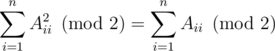
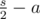 других пар. Среди них, для
других пар. Среди них, для 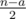 пар оба числа принадлежат
пар оба числа принадлежат 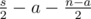 пар никакие из чисел не принадлежат
пар никакие из чисел не принадлежат 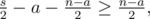
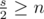 , как и дано в условии.
, как и дано в условии.
 .
. .
.
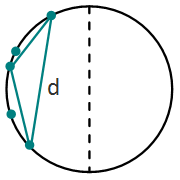
 из-за сортировки.
из-за сортировки.
 ,
, 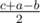 ,
, 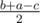 . Если бы в задаче просили проверить только, можно ли построить такую молекулу, то хватало бы проверить нестрогое неравенство треугольника для
. Если бы в задаче просили проверить только, можно ли построить такую молекулу, то хватало бы проверить нестрогое неравенство треугольника для 
 , то нетрудно посчитать, что с помощью
, то нетрудно посчитать, что с помощью 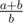 и
и 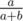 . То есть прибавление одного элемента эквивалентно одному шагу алгоритма Эвклида для числителя и знаменателя в обратном направлении. Значит, ответ равняется количеству шагов стандартного алгоритма Эвклида.
. То есть прибавление одного элемента эквивалентно одному шагу алгоритма Эвклида для числителя и знаменателя в обратном направлении. Значит, ответ равняется количеству шагов стандартного алгоритма Эвклида.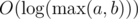 . Авторы задачи:
. Авторы задачи: 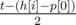 секунд, затем налево
секунд, затем налево 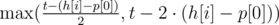 . Дальше двигаем указатель на первую несчитанную дорожку, и повторяем алгоритм для
. Дальше двигаем указатель на первую несчитанную дорожку, и повторяем алгоритм для 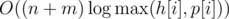 . Авторы задачи:
. Авторы задачи: 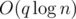 . Автор задачи:
. Автор задачи: 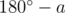 . Их сумма равна
. Их сумма равна 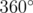 , так как многоугольник выпуклый. Тогда выполняется следующее равенство:
, так как многоугольник выпуклый. Тогда выполняется следующее равенство: 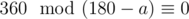 .
.

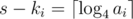
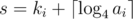
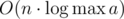 .
.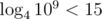 . Поэтому достаточно найти первый подходящий квадрат со стороной от
. Поэтому достаточно найти первый подходящий квадрат со стороной от 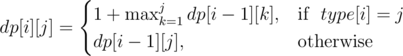
 .
. , сразу же обновляем наибольший возможный нисходящий поток из
, сразу же обновляем наибольший возможный нисходящий поток из 


 (сверху-направо)
(сверху-направо) 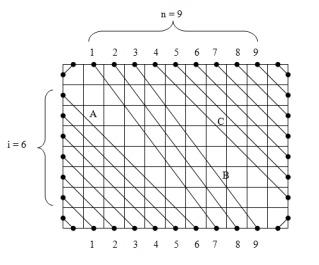
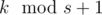 (сверху-направо отрезки продолжаются как соответствующие слева-вниз отрезки). Это можно описать перестановкой
(сверху-направо отрезки продолжаются как соответствующие слева-вниз отрезки). Это можно описать перестановкой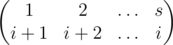
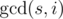 циклов длины
циклов длины 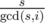 , то есть все циклы одинаковой длины. Обозначим каждый тип отрезка одним символом (на рисунке A, B, C). Тогда не только длина, но и строки, соответствующие циклам, тоже равны, но могут быть циклически сдвинуты, когда мы их нашли (именно здесь важно направление циклов). Кроме того, мы уже знаем, как выглядит такая строка из конечного прямоугольника. Поэтому нам нужно сравнить строки всех оставшихся циклов из данного прямоугольника с этой строкой, беря во внимание сдвиги как инвариант. Для каждой строки это можно сделать за линейное время, например, с помощью алгоритма Кнута-Морриса-Пратта. Когда для каждого цикла находим значение циклического сдвига, перестанавливаем ряды и столбцы по соответствию с конечным прямоугольником.
, то есть все циклы одинаковой длины. Обозначим каждый тип отрезка одним символом (на рисунке A, B, C). Тогда не только длина, но и строки, соответствующие циклам, тоже равны, но могут быть циклически сдвинуты, когда мы их нашли (именно здесь важно направление циклов). Кроме того, мы уже знаем, как выглядит такая строка из конечного прямоугольника. Поэтому нам нужно сравнить строки всех оставшихся циклов из данного прямоугольника с этой строкой, беря во внимание сдвиги как инвариант. Для каждой строки это можно сделать за линейное время, например, с помощью алгоритма Кнута-Морриса-Пратта. Когда для каждого цикла находим значение циклического сдвига, перестанавливаем ряды и столбцы по соответствию с конечным прямоугольником. , где
, где 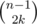 способами. То же самое сделаем и с верхними и нижними границами, это можно сделать
способами. То же самое сделаем и с верхними и нижними границами, это можно сделать 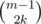 способами. Заметим, что каждая пара таких размещений однозначно определяет одно искомое расположение, и все такие расположения можно определить одной парой размещений. Поэтому ответом является
способами. Заметим, что каждая пара таких размещений однозначно определяет одно искомое расположение, и все такие расположения можно определить одной парой размещений. Поэтому ответом является 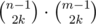 . Так как
. Так как 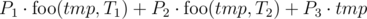 . Переменная res и является ответом задачи.
. Переменная res и является ответом задачи.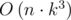 ). Идём по всем возможным позициям
). Идём по всем возможным позициям 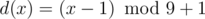 . Заметим, что для задачи не важно,
. Заметим, что для задачи не важно, 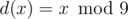 .
.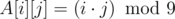 : чтобы знать значение
: чтобы знать значение 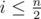 . И так для каждого
. И так для каждого  . Вся их сумма — искомое количество (
. Вся их сумма — искомое количество (
