DivII A. Печеньки
Самый лёгкий способ решить задачу — сперва посчитать всю сумму чисел, и затем посчитать количество чётных разностей между этой суммой и каждым числом. Однако маленькое наблюдение позволит написать решение немного эффективней: помимо суммы (sum) посчитаем также, сколько среди данных чисел есть чётных (even) и нечётных (odd). Тогда, если сумма нечётна, то ответ — odd, иначе — even. Время O(n), память O(1).
DivII B. Шнурки и шестиклассники
Маленькие ограничения позволяют нам написать решение «в лоб». Будем хранить данный граф в матрице смежности, и симулировать происходящее. Также будем хранить степень каждой вершины отдельно, чтобы быстро находить детей, которые связаны только одним шнурком. Тогда при каждой итерации удаляем все вершины со степенью 1 и все грани, которые соединяются с этими вершинами; продолжаем до тех пор, пока не останется таких вершин. Ответом будет количество произведённых итераций. Время O(n3), память O(n2).
DivII C / DivI A. Статуи
Произведём симуляцию падения статуй. При каждой итерации будем сдвигать все статуи на одну клетку вниз. Перед каждым ходом (итерацией) будем получать список всех полей, куда Маша может пойти (до того, как статуи передвинутся на одну клетку вниз), используя список тех полей, куда она могла придти с прошлого хода (единственное, из полей с прошлого хода можно использовать только те, в которые после конца прошлого хода не переместилась статуя). Логично, что через 8 любых ходов на доске не останется ни одной статуи. Поэтому, если список доступных Маше полей после 8-ого хода не пуст, то она может добраться до Ани, потому что дальше её ходы ничто не ограничивает. Время O(9· 83) = O(1), память O(82) = O(1).
DivII D / DivI B. Строка
Вначале ликвидируем случай невозможности — такой строки нет, если k больше, чем количество подстрок, т.е.  , где n — длина строки.
, где n — длина строки.
Теперь заметим, что для каждой буквы мы можем быстро оценить, сколько подстрок начинаются именно с этой буквы. Действительно, если буква стоит на позиции i (нумеруя с 1), то количеством подстрок, начинающихся с позиции i, является n - i + 1. Тогда количество строк, которые начинаются с конкретной буквы, будет сумма всех таких значений для позиций, в которых стоит эта буква.
Далее, используя найденную информацию, не сложно выяснить, с какой буквы будет начинаться нужная подстрока (потому что в слове при лексикографическом сравнении буквы слева важнее, чем буквы справа). Теперь заметим, что тоже самое рассуждение мы можем применить и для следующей буквы нужного слова, только теперь нужно проверить только такие буквы, которые следуют после первой буквы слова. Таким образом, мы повторяем итерации и для 3-ей, 4-ой, ... букв до тех пор, пока не найдём нужную строку. Чтобы не искать каждый раз нужные позиции, будем хранить их отдельно; при каждой итерации сдвигать их на одну позицию направо и исполнять алгоритм только для них, а после нахождения i-того символа убирать те позиции, буквы в которых не равны с найденным символом. Время благодаря k ≤ 105 не квадратичное (самому ещё не получилось доказать), память O(n).
Также задачу можно было решить с помощью хэшей или суффиксного массива.
DivII E / DivI C. Игра с прямоугольниками
Рассмотрим все левые и правые границы всех k внутренних прямоугольников, вместе их 2k. Присвоим им произвольные 2k координат между левой и правой стороной данного прямоугольника, это можно сделать 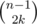 способами. То же самое сделаем и с верхними и нижними границами, это можно сделать
способами. То же самое сделаем и с верхними и нижними границами, это можно сделать 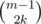 способами. Заметим, что каждая пара таких размещений однозначно определяет одно искомое расположение, и все такие расположения можно определить одной парой размещений. Поэтому ответом является
способами. Заметим, что каждая пара таких размещений однозначно определяет одно искомое расположение, и все такие расположения можно определить одной парой размещений. Поэтому ответом является 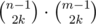 . Так как n и m не больше 1000, то коэффициенты можно посчитать с помощью треугольника Паскаля (не забывая вычислять по данному модулю). Время O(max(n, m)2), память O(max(n, m)2).
. Так как n и m не больше 1000, то коэффициенты можно посчитать с помощью треугольника Паскаля (не забывая вычислять по данному модулю). Время O(max(n, m)2), память O(max(n, m)2).
DivI D. Числа
У меня эта задача ассоциировалась с атомами и молекулами. :) Представим, что каждое из чисел имеет две связи, где связь соединяется с другой по заданным правилам. Тогда решение существует тогда и только тогда, когда все связи соединены, и из каждого элемента по связям можно дойти до любого другого элемента; также решения не существует, если присутствуют числа x, x + 2, но x + 1 не присутствует.
Пусть у нас есть числа a, a + 1, ..., b, тогда количество связей у них 2|a|, 2|a + 1|, ..., 2|b|, где |x| — количество чисел x. Ясно, что 2|a| связей от 2|a + 1| «съедают» элементы a. У a + 1 свободными остаются p = 2|a + 1| - 2|a| связей. Аналогично, эти p связей соединяются с a + 2 элементами и т.д. В конце концов, если у b - 1 свободными остаются q связей, то должно быть q = 2|b|, чтобы завершить цепочку. Остаётся только проверить все эти соотношения (учитывая то, что цепочку нельзя завершить раньше, чем не истрачены все связи — то есть, вычисляемый p не может быть 0). Время  (т.к. данные числа нужно отсортировать), память O(n). Для простоты вычислений можно ещё заметить, что 2|a| можно заменить на |a|, из-за этого ничего не изменится.
(т.к. данные числа нужно отсортировать), память O(n). Для простоты вычислений можно ещё заметить, что 2|a| можно заменить на |a|, из-за этого ничего не изменится.
DivI E. День рождения
См. хороший разбор здесь.











Here is my code for "Students and Shoelaces" problem, please let me know if I can optimize it in someway...
My submissions
Could you help me explain why the time complexity in problem C (div 2) is O(9.8^3)
I am having difficulty in finding the solution for the "Students and Shoelaces" solution because the output the of the Codeforces compiler for Testcase#3 is different from the output my offline text editor (Sublime Text) is giving (my text editor is giving the right answer whereas the codeforces compiler is giving a wrong answer). The Codeforces compiler is also giving a error message for this testcase :
Diagnostics detected issues [cpp.clang++-diagnose]: C:\Program Files (x86)\Microsoft Visual Studio\2017\Enterprise\VC\Tools\MSVC\14.11.25503\include\vector:1802:11: runtime error: addition of unsigned offset to 0x12b01340 overflowed to 0x08a60930SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior C:\Program Files (x86)\Microsoft Visual Studio\2017\Enterprise\VC\Tools\MSVC\14.11.25503\include\vector:1802:11 in``So I read that this error message is given when there is some out of bound cases. To fix that I modified the code but that modification is giving me wrong answer for Testcase#51.
My initial submission : https://codeforces.net/contest/129/submission/78633028
My modified submission : https://codeforces.net/contest/129/submission/78634662
Is there something wrong with my logic or my code? How can I fix it?
Thank you for your time.
PS : Here is a short explanation of my code :
adj[i]is a map of all the students connected to theith student.mp[i]is used to store students withinumber of connections. Thereforemp[1]stores the students which have 1 connection. Thewhileloop simulates the entire process. The vectorvstores the students which will be having 1 connection in the next round i.e. if a student had 2 connections and one of the connected student got kicked in roundithen the number of connections reduces to 1 connection, which means that this student will have to reprimanded in roundi + 1. Therunvariable checks if the current group of students have already been counted; hence when the new round of students with 1 connection is considered, therunis reset tofalseUPD : Problem fixed — I had to change my approach as it was not covering many corner cases. I used a queue to simulate the process. Here is a link to the solution : 83548603