CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
43:01:45
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
870A - Поиск красивых чисел Идея, подготовка, разбор komendart
870B - Максимум максимума из минимумов Идея DPR-pavlin, подготовка, разбор mHuman
870C - Максимальное разбиение Идея, подготовка, разбор komendart
870D - Что-то там c xor запросами Идея, подготовка, разбор mHuman
870E - Точки, прямые и неоригинальные названия Идея, подготовка, разбор komendart
870F - Пути Идея, подготовка, разбор komendart
871E - Восстановление дерева Идея MikeMirzayanov, подготовка fcspartakm, разбор mHuman
Также спасибо координатору KAN, тестерам ifsmirnov, vintage_Vlad_Makeev, AlexFetisov и другим людям, участвовавшим в подготовке задач.
Код (C++) 31365874
Код (Python) 31365844
Код 31366254
Код 31365909
Код 31366223
Код 31365959
Код 31366002
Код 31368704
Всем привет!
Я не знаю, возможно, эта тема где-то уже поднималась, но быстрый гуглинг не помог.
Такое ощущение, что стандартная хеш-функция для целых чисел в gcc работает плохо (для Visual C++ все нормально).
Для 0 ≤ x ≤ 232 - 1
std::hash<int>()(x) == x
std::hash<long long>()(x) == x
Для остальных чисел верно
std::hash<long long>()(x + (1LL << 32)) == std::hash<long long>()(x)
Например, код ниже работает в запуске на Codeforces более 10 секунд, потому что хеши всех чисел равны нулю.
#include <iostream>
#include <unordered_set>
using namespace std;
int main() {
unordered_set<long long> d;
int n = 1e5;
long long t = 1LL << 32;
for (int i = 0; i < n; i++) {
d.insert(i * t);
}
cout << d.size() << endl;
}
Можно ли что-то с этим сделать без написания собственной хеш-функции?
Когда-нибудь я расположу C и D в правильном порядке :)
675A - Бесконечная последовательность
Во-первых, в случае c = 0 мы должны вывести YES если a = b, иначе вывести NO.
Если b принадлежит последовательности, то b = a + k * c, где k является неотрицательным целым числом.
Поэтому ответ YES если (b - a) / c является неотрицательным целым, иначе ответ NO.
#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b, c;
cin >> a >> b >> c;
if (c == 0) {
if (a == b) cout << "YESn";
else cout << "NOn";
} else {
if ((b - a) % c == 0 && (b - a) / c >= 0) cout << "YESn";
else cout << "NOn";
}
}
x a y
b m c
z d w
Число в центре может быть любым от 1 до n, потому что оно лежит внутри всех квадратов 2 × 2. Поэтому мы можем найти ответ с фиксированным числом в центре и потом домножить его на n.
Переберем все возможные x. Суммы в каждом квадрате 2 × 2 одинаковы, поэтому x + b + a + m = y + c + a + m и y = x + b - c.
Аналогично, z = x + a - d и w = a + y - d = z + b - c.
Квадрат с данными числам легален, если 1 ≤ y, z, w ≤ n. Мы должны просто проверить это.
Это было решение за O(n). Существует также решение за O(1).
#include <iostream>
using namespace std;
int main() {
int n, a, b, c, d;
cin >> n >> a >> b >> c >> d;
long long ans = 0;
for (int x = 1; x <= n; x++) {
int y = x + b - c;
int z = x + a - d;
int w = a + y - d;
if (1 <= y && y <= n && 1 <= z && z <= n && 1 <= w && w <= n) {
ans++;
}
}
ans *= n;
cout << ans << endl;
}
У нас есть массив ai и мы должны обнулить все числа внутри него с помощью минимального количества операций. Сумма всех чисел в массиве равна нулю.
Мы можем разделить массив на части с нулевой суммой, состоящие из последовательных элементов (первый и последний элемент считаются последовательными). Если часть имеет длину l, то мы можем обнулить ее с помощью l - 1 операции.
Следовательно, если мы сложим количество операций, то получим, что ответ равен n - k, где k — количество частей. Для того, чтобы ответ был минимальным, мы должны максимизировать k.
Одна из частей состоит из префикса и, возможно, суффикса массива. Остальные части являются подмассивами.
Давайте посчитаем префиксные суммы. Заметим, что префиксные суммы перед частями-подмассивами равны между собой, так как сумма чисел в каждой части равна нулю.
Следовательно, ответ равен n - f, где f — количество вхождений самого частого элемента среди префиксных сумм.
Бонус: как взламывать решения с переполнением?
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
int n;
cin >> n;
map<long long, int> d;
long long sum = 0;
int ans = n - 1;
for (int i = 0; i < n; i++) {
int t;
cin >> t;
sum += t;
d[sum]++;
ans = min(ans, n - d[sum]);
}
cout << ans << endl;
}
У нас есть двоичное дерево поиска и мы должны уметь быстро добавлять в него числа.
Пусть сейчас мы должны добавить число x. Найдем ранее добавленные числа l < x < r такие, что l максимально возможное, а r минимально возможное. Если только одно из этих чисел существует, то рассуждения почти не меняются. Мы можем найти l и r, например, с помощью std::set и upper_bound, если вы пишете на C++.
Мы должны сохранять отсортированный обход дерева, так как это свойство двоичного дерева поиска. Поэтому x должно быть правым потомком вершины l или левым потомком вершины r.
Пусть l не имеет правого потомка и r не имеет левого потомка. Тогда наименьший общий предок l и r (lca) не совпадает с l и r. Но тогда lca находится между l и r, а это невозможно, так как l максимально, а r минимально. Получается противоречие, поэтому l имеет правого потомка или r имеет левого потомка. Следовательно, мы точно знаем, кто из них станет предком x.
Это всё. Сложность решения  .
.
#include <iostream>
#include <set>
#include <map>
using namespace std;
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
set<int> numbers;
map<int, int> left;
map<int, int> right;
int n, v;
cin >> n >> v;
numbers.insert(v);
for (int i = 0; i < n - 1; i++) {
cin >> v;
auto it = numbers.upper_bound(v);
int result;
if (it != numbers.end() && left.count(*it) == 0) {
left[*it] = v;
result = *it;
} else {
it--;
right[*it] = v;
result = *it;
}
numbers.insert(v);
cout << result;
if (i == n - 2) cout << 'n';
else cout << ' ';
}
}
675E - Электрички и статистика
Введем индексацию с нуля. Уменьшим каждый ai на единицу. Также сделаем an - 1 равным n - 1.
Пусть dpi — сумма кратчайших путей из i в i + 1... n - 1.
dpn - 1 = 0
dpi = dpm - (ai - m) + n - i - 1, где m лежит между i + 1 и ai и am максимально. Мы можем найти m с помощью дерева отрезков / дерева Фенвика / разреженной таблицы.
Ответ равен сумме всех dpi.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1 << 18;
pair<int, int> tree[maxn * 2];
void build(const vector<int> &a, int n) {
for (int i = 0; i < n; i++) tree[maxn + i] = {a[i], i};
for (int i = maxn - 1; i > 0; i--)
tree[i] = max(tree[i * 2], tree[i * 2 + 1]);
}
int get(int l, int r) {
pair<int, int> ans{-1, -1};
for (l += maxn, r += maxn + 1; l < r; l >>= 1, r >>= 1) {
if (l & 1) ans = max(ans, tree[l++]);
if (r & 1) ans = max(ans, tree[--r]);
}
return ans.second;
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
int n;
cin >> n;
vector<int> a(n);
a[n - 1] = n - 1;
for (int i = 0; i < n - 1; i++) {
cin >> a[i];
a[i]--;
}
build(a, n);
vector<long long> dp(n);
long long ans = 0;
dp[n - 1] = 0;
for (int i = n - 2; i >= 0; i--) {
int m = get(i + 1, a[i]);
dp[i] = dp[m] - (a[i] - m) + n - i - 1;
ans += dp[i];
}
cout << ans << 'n';
}
Всем привет!
Codeforces Round #353 (Div. 2) состоится завтра, 16 мая в 19:35 MSK. Я постарался сделать интересные задачи, надеюсь, они вам понравятся.
Хочу сказать спасибо GlebsHP за помощь при подготовке задач и MikeMirzayanov за Codeforces и Polygon.
Удачи!
UPD Разбалловка 500-1000-1500-2000-2500
UPD Разбор
UPD Поздравляем победителей!
Div. 2
Div. 1
Оптимально делать наибольший возможный шаг каждый раз. Поэтому слоник должен сделать сначала некоторое количество шагов на расстояние 5, а затем один или ноль шагов на меньшее расстояние. Следовательно, ответ равен 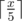 .
.
Решение 15550796
Нам дан массив, состоящий только из нулей и единиц. Мы должны разделить его на части, в каждой из которых ровно одна единица.
Особый случай: когда массив состоит только из нулей ответ равен нулю.
Рассмотрим общий случай. Во-первых нули на префиксе относятся к первому куску, нули на суффиксе относятся ко второму куску. Во-вторых, между каждой парой соседних единиц должно быть одно и только одно разделение частей. Между соседними единицами с индексами a < b всего b - a вариантов разделения. Поэтому мы должны перемножить эти значения для всех пар соседних единиц.
Бонус: каким является максимальный ответ при n ≤ 100?
Решение 15550806
Первый радиус равен нулю или расстоянию от первого фонтана до какого-то цветка. Переберем все эти числа. Второй радиус будет равен максимальному из расстояний от второго фонтана до цветка, который не принадлежит кругу с первым радиусом. Теперь мы должны выбрать вариант с минимальным r12 + r22
Бонус: Я описал решение за O(n2). Можете ли вы решить задачу за O(nlogn)?
Решение за O(n2) 15550812
Решение за O(nlogn) 15550822
Ответ равен одному, когда все координаты x или все координаты y совпадают.
Когда ответ равен двум? Переберем все пары точек. Пусть первая точка является началом ломаной, вторая концом ломаной. Только одна или две таких ломаных с двумя звеньями существуют. Они образуют прямоугольник с противоположными углами в первой и второй точке. Мы можем просто проверить принадлежность третьей точки прямоугольнику.
Иначе ответ всегда равен трем. Давайте построим вертикальные прямые через самую левую и через самую правую точки. Через третью точку построим горизонтальную прямую. Теперь, если мы удалим некоторые лишние лучи, получим подходящую ломаную.
Решение 15550843
У нас есть массив a
Давайте посчитаем массив 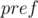 (
(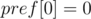 ,
, 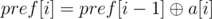 ).
).
Xor подмассива 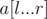 равен
равен 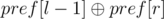 .
.
Теперь запрос (l, r) заключается в подсчете количества пар i, j (l - 1 ≤ i < j ≤ r) 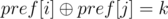 .
.
Пусть мы знаем ответ на запрос (l, r) и знаем для всех v cnt[v] — количество вхождений v в 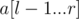 .
.
Мы можем обновить за O(1) ответ и cnt если мы изменим правую или левую границу запроса на 1.
Поэтому мы можем решить задачу оффлайн за 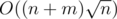 с помощью корневой эвристики (алгоритм Мо).
с помощью корневой эвристики (алгоритм Мо).
Решение 15550846
Привет!
Завтра, 23 января в 18:35 MSK состоится Codeforces Round #340 (Div. 2). Это мой первый раунд, надеюсь, вам понравятся задачи.
Спасибо GlebsHP за помощь при подготовке задач, Delinur за перевод условий и MikeMirzayanov за Codeforces и Polygon.
Всем удачи!
UPD Разбалловка 500-1000-1250-1750-2750
UPD Разбор
UPD Поздравляем победителей!
Div. 2
Div. 1
| Название |
|---|









